4 Конструктивная схема программного обеспечения

В данном разделе приводится описание конструктивной схемы и ее составных компонентов программного обеспечения для решения систем алгебраических уравнений методом ортогонализации и проведения численных экспериментов.

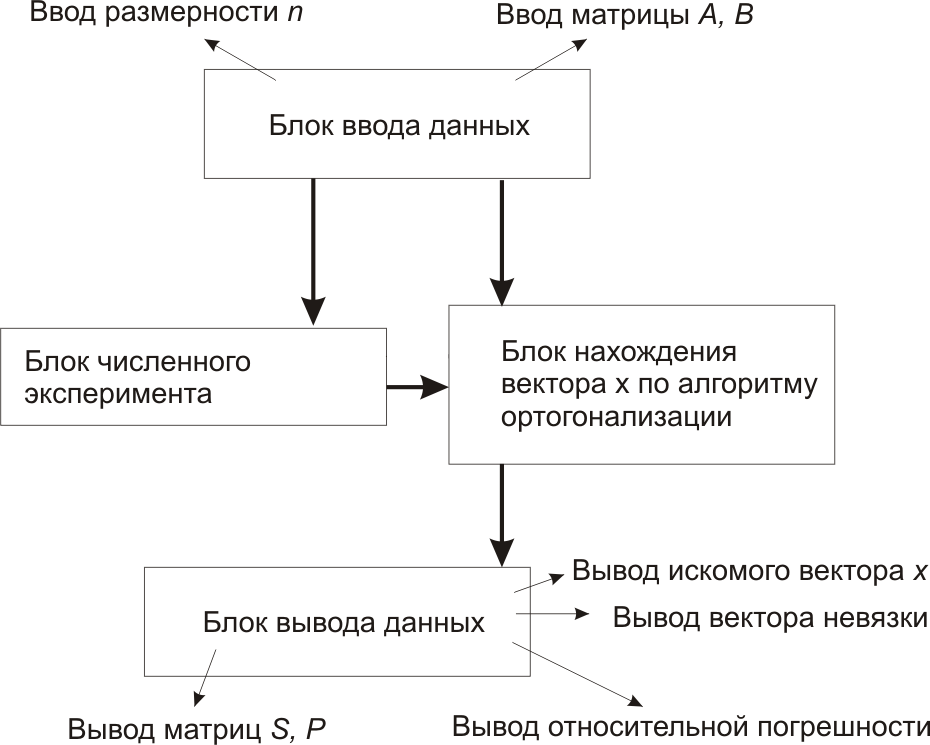
Рисунок 4.1 - Конструктивная схема программного обеспечения

Блок "Ввод данных" предназначен для обеспечения выполнения следующих функций: ввод размерность матрицы и ее элементов, вектор точных решений. После ввода точных решений можно автоматически произвести расчет вектора В.

Блок "Нахождение вектора Х" предназначен для расчета искомого вектора по алгоритму, приведенному в разделе 3.

Блок "Численные эксперименты" предназначен для проведения экспериментов: вычисление относительной погрешности и построение графика зависимости погрешности от размерности матрицы.

Блок "Вывод результатов" обеспечивает вывод полученных результатов: вектора решений, относительной погрешности.

5. Численные эксперименты и результаты

В разделе приводится описание численных экспериментов и их результатов.

Цель проведения экспериментов состояла в изучении поведения равномерной нормы относительной погрешности решения на заданном типе матрицы системы и размерности системы в пределах от 4 до 15. Эксперименты проводились следующим образом. По введенному известному решению x формировалась правая часть системы. Затем построенная система решалась, т.е. находилось решение . Величина нормы относительной погрешности рассчитывалась по формуле . На рисунке 2 приводится кривая изменения в зависимости от размерности исходной системы.

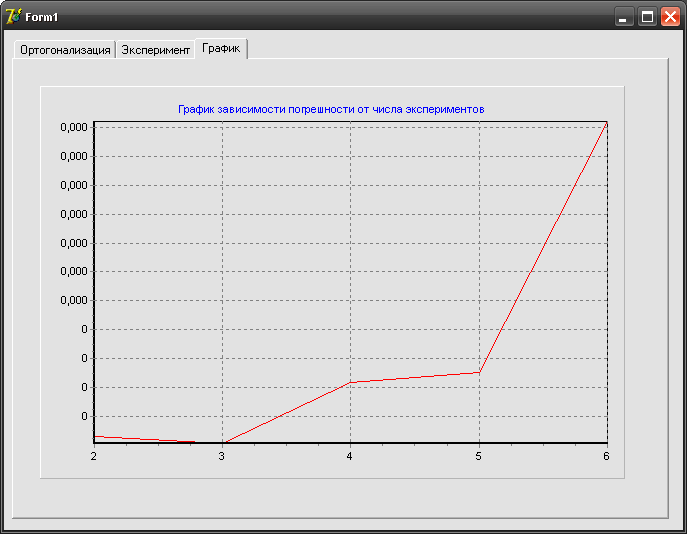
Рисунок 2 – График зависимости от размерности матрицы

Заключение

Все задания курсовой были выполнены. Разработан алгоритм метода ортогонализации, спроектирована и реализована программная система, реализующая нахождение решении системы линейных алгебраических уравне ний и обеспечивающая возможность проведения численных экспериментов.

Эксперименты показали, ошибка метода в основном связана с вычисле нием скалярных произведений. Эта ошибка возрастает с ростом размерности системы уравнений.

Конструктивная схема составлена таким образом, что позволяет проводить

модификацию программного обеспечения без изменения основной схемы.

Программное обеспечение может использоваться в процессе изучения в

соответствующем разделе вычислительной математики, как дополнительный инструмент в освоении и изучении метода ортогонализации.

Список использованных источников

1 Ibooks.ru [Электронный ресурс]: электронная библиотечная система: база данных содержит электронные учебники по высшей школе/ЗАО «Айбукс».Спб., 2010. Режим доступа: http:/www.ibooks.ru

2 Университетская библиотека Online [Электронный ресурс]: электронная библиотечная система: база данных содержит электронные учебники для вузов/ ООО «Директмедиа Паблишинг».М., 2006. Режим доступа: http: /www. biblioclub.ru

3 Ващенко, Г.В. Вычислительная математика. Основы конечных методов решения систем линейных алгебраических уравнений/ Г. В. Ващенко – Красноярск.: СибГТУ., 2005 – 80 с.

4 Тыртышников, Е.Е. Методы численного анализа/ Е.Е. Тыртышников. М.: Academia, 2007. 320 с.

Приложение

Приложение А. Исходные тексты основных процедур программы

var

Form1: TForm1;

Razmer:integer;

A,R,S,s1,B,C:array[1..100,1..100] of single;

D:array[1..100,1..2] of single;

tmp,sp,SS,x,x1,y1,max1,max2,stek:single;

i,j,k,p,KolExp,h,n1,kum:integer;

st, t: TLineSeries;

implementation

{$R *.dfm}

{ TForm1 }

procedure TForm1.Edit1Change(Sender: TObject);

begin

Razmer:=StrToInt(Edit1.Text);

StringGrid1.RowCount:=Razmer;

StringGrid1.ColCount:=Razmer;

StringGrid2.RowCount:=Razmer;

StringGrid3.RowCount:=Razmer;

end;

procedure TForm1.Button1Click(Sender: TObject);

begin

try

For i:=1 to Razmer do

begin

for j:=1 to Razmer do

begin

A[i,j]:=StrToFloat(StringGrid1.Cells[j-1,i-1]);

end;

end;

for i:=1 To Razmer do

begin

A[i,Razmer+1]:=StrToFloat(StringGrid2.Cells[0,i-1]);

end;

A[Razmer+1,RazMer+1]:=1;

except

ShowMessage('Заполните матрицы');

exit;

end;

//-------------------------------------------------

for i:=1 to (razmer+1) do

begin

r[1,i]:=a[1,i];//r1=a1

end;

tmp:=0;

for i:=1 to (razmer+1) do

begin

tmp:=tmp+sqr(r[1,i]);

end;

tmp:=sqrt(tmp); // ||r1||

//--------------------------------------------------

for i:=1 to (razmer+1) do

begin

s[1,i]:=r[1,i]/tmp;// s1=r1/sqrt(r1,r1)

end;

//------------------------------------------------------

For k:=2 to (Razmer+1) do

begin

for i:=1 to k-1 do

begin

//--------------------------------

SP:=0;

for j:=1 to (Razmer+1) do//sp=(Ak,Si)

begin

SP:=SP+A[k,j]*S[i,j];

end;//j

//---------------------------------

For p:=1 To (Razmer+1) do

begin

S1[i,p]:=SP*S[i,p]

end;//p

end;//i

//------вычисление компонент вектора Rk--------

for j:=1 to (Razmer+1) do

begin

SS:=0;

for i:=1 to (k-1) do

begin

SS:=SS+S1[i,j];

end;//i

R[k,j]:=A[k,j]-SS;

end;//j

//--------Формирование вектора Sk----------------

sp:=0;

for i:=1 to (Razmer+1) do

begin

sp:=sp+R[k,i]*R[k,i]; //скалярное произведение

end;//i

for p:=1 to (Razmer+1) do

begin

S[k,p]:=R[k,p]/sqrt(SP);

end;//p

end;//k

//-------формирование и вывод решения---------------

for j:=1 to (Razmer) do

begin

StringGrid3.Cells[0,j-1]:=FloatToStr((R[Razmer+1,j]/R[Razmer+1,Razmer+1])*(-1));

end;

end;

procedure TForm1.FormCreate(Sender: TObject);

begin

st := TLineSeries.Create(nil);

SpinEdit2.Value:=2;

Razmer:=SpinEdit2.Value;

StringGrid4.RowCount:=Razmer;

StringGrid4.ColCount:=Razmer;

StringGrid5.RowCount:=Razmer;

StringGrid6.RowCount:=Razmer;

StringGrid7.RowCount:=Razmer;

end;

procedure TForm1.Button2Click(Sender: TObject);

begin

KolExp:=SpinEdit1.Value;

Razmer:=SpinEdit2.Value;

StringGrid4.RowCount:=Razmer;

StringGrid4.ColCount:=Razmer;

StringGrid5.RowCount:=Razmer;

StringGrid6.RowCount:=Razmer;

StringGrid7.RowCount:=Razmer;

for h:=1 to KolExp do

begin

randomize;

for i:=1 to razmer do

begin

for j:=1 to razmer do

begin

StringGrid4.Cells[j-1,i-1]:=IntToStr(random(10));

end;

StringGrid7.Cells[0,i-1]:=IntToStr(random(10));

end;

For i:=1 to Razmer do

begin

for j:=1 to Razmer do

begin

A[i,j]:=StrToFloat(StringGrid4.Cells[j-1,i-1]);

end;

B[1,i]:=StrToFloat(StringGrid7.Cells[0,i-1])

end;

for i:=1 to razmer do

begin

for j:=1 to razmer do

begin

c[i,j]:=0;

for k:=1 to razmer do

begin

c[i,j]:=c[i,j]+a[i,k]*b[j,k];

end;

end;

StringGrid5.Cells[0,i-1]:=FloatToStr(c[i,1]);

end;

for i:=1 To Razmer do

begin

A[i,Razmer+1]:=StrToFloat(StringGrid5.Cells[0,i-1]);

end;

A[Razmer+1,RazMer+1]:=1;

//-------------------------------------------------

for i:=1 to (razmer+1) do

begin

r[1,i]:=a[1,i];//r1=a1

end;

tmp:=0;

for i:=1 to (razmer+1) do

begin

tmp:=tmp+sqr(r[1,i]);

end;

tmp:=sqrt(tmp); // ||r1||

//--------------------------------------------------

for i:=1 to (razmer+1) do

begin

s[1,i]:=r[1,i]/tmp;// s1=r1/sqrt(r1,r1)

end;

//------------------------------------------------------

For k:=2 to (Razmer+1) do

begin

for i:=1 to k-1 do

begin

//--------------------------------

SP:=0;

for j:=1 to (Razmer+1) do//sp=(Ak,Si)

begin

SP:=SP+A[k,j]*S[i,j];

end;//j

//---------------------------------

For p:=1 To (Razmer+1) do

begin

S1[i,p]:=SP*S[i,p]

end;//p

end;//i

//------вычисление компонент вектора Rk--------

for j:=1 to (Razmer+1) do

begin

SS:=0;

for i:=1 to (k-1) do

begin

SS:=SS+S1[i,j];

end;//i

R[k,j]:=A[k,j]-SS;

end;//j

//--------Формирование вектора Sk----------------

sp:=0;

for i:=1 to (Razmer+1) do

begin

sp:=sp+R[k,i]*R[k,i]; //скалярное произведение

end;//i

for p:=1 to (Razmer+1) do

begin

S[k,p]:=R[k,p]/sqrt(SP);

end;//p

end;//k

//-------формирование и вывод решения---------------

for j:=1 to (Razmer) do

begin

StringGrid6.Cells[0,j-1]:=FloatToStr((R[Razmer+1,j]/R[Razmer+1,Razmer+1])*(-1));

end;

//---------------delta---------

x:=0;

x1:=0;

Application.ProcessMessages;

max1:=0;

max2:=0;

for i:=1 to razmer do

begin

stek:=StrToFloat(StringGrid6.Cells[0,i-1])-StrToFloat(StringGrid7.Cells[0,i-1]);

if stek>max1 then max1:=stek;

stek:=StrToFloat(StringGrid7.Cells[0,i-1]);

if stek>max2 then max2:=stek;

end;

D[h,1]:=max1/max2;

D[h,2]:=razmer;

StringGrid4.RowCount:=Razmer;

StringGrid4.ColCount:=Razmer;

StringGrid5.RowCount:=Razmer;

StringGrid6.RowCount:=Razmer;

StringGrid7.RowCount:=Razmer;

inc(razmer);

end;

with Chart1 do

begin

AllowZoom:=true;

View3D:=False;

Title.Text.Clear;

Title.Text.Add('График зависимости погрешности от числа экспериментов');

st.Clear;

st.Title := 'Chart Linie 1';

st.ParentChart := Chart1;

for i := 1 to KolExp do

begin

x1 :=D[i,1] ;

y1:=d[i,2];

st.AddXY(y1,x1);

end;

end;

end;

procedure TForm1.SpinEdit2Change(Sender: TObject);

begin

Razmer:=SpinEdit2.Value;

StringGrid4.RowCount:=Razmer;

StringGrid4.ColCount:=Razmer;

StringGrid5.RowCount:=Razmer;

StringGrid6.RowCount:=Razmer;

StringGrid7.RowCount:=Razmer;

end;

end.