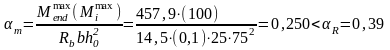5.4 Перераспределение моментов под влиянием образования пластических шарниров в ригеле

Практически перераспределение изгибающих моментов под влиянием пластических деформаций заключается в уменьшении примерно на 30% опорного момента М_в, соответствующего схемам загружения 1+4. К эпюре моментов по схеме 1+4 добавляется треугольная выравнивающая эпюра с максимальной ординатой ниже опоры В:

ΔМ_b=0,3·М_b¹⁺⁴=0,3·(180,5+384,1) = 170 кН·м.

Если же разность моментов (М_b¹⁺⁴– М_b¹⁺²)= (180,5+384,1) - (180,5+164,2) =219,9 <0,3·М_b¹⁺⁴=170, то ΔМ_b=(М_b¹⁺⁴– М_b¹⁺²). В нашем случае (М_b¹⁺⁴– М_b¹⁺²)>0,3·М_b¹⁺⁴, следовательно, ΔМ_b=0,3·М_b¹⁺⁴=170 кН·м.

Кроме того, следуя методике перераспределения усилий, к эпюре моментов по схеме 1+4 необходимо добавить треугольную эпюру, расположенную во втором и третьих пролетах с ординатой над опорой С:

С=ΔМ_с= -[|М_b¹⁺⁴- ΔМ_b| - |М_с¹⁺⁴|]= -[|180,5+384,1-170| - |180,5+108,3|]=-105,8 кН·м.

По данным таблиц 4 и 5 строятся эпюры изгибающих моментов и поперечных сил при различных комбинациях схем загружения. При этом постоянная нагрузка по схеме I участвует во всех комбинациях: 1+2; 1+3; 1+4.

5.5. Вычисление моментов в ригеле по грани колонны.

Расчетными на опоре являются сечения ригеля по грани колонны. В этих сечениях максимальные изгибающие моменты определяются по формуле:

,

где - граневый изгибающий момент у опоры В слева (л) или справа (п) от нее при схеме загружения 1+m (m=2,3,4).

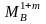- изгибающий момент на опоре В.

- поперечная сила на опоре В справа (п) или слева (л) от нее.

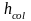- размер поперечного сечения колонны

.

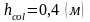На опоре В при схеме загружения 1+4 опорный момент по грани колонны не всегда оказывается расчетным, максимальным по абсолютному значению. Он может оказаться расчетным при схеме загружения 1+2 или 1+3. Поэтому необходимо определить моменты по всем схемам загружения.

Вычисление граневых изгибающих моментов у опоры В слева:

Схема загружения 1+4:

Схема загружения 1+3:

Схема загружения 1+2:

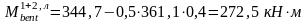
В данном случае для первого пролета расчетный граневый момент принимается равным .

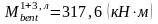Вычисление граневых изгибающих моментов у опоры В справа и у опоры С слева.

Схема загружения 1+4:

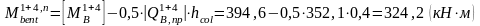
Схема загружения 1+3:

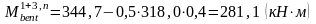
Схема загружения 1+2:

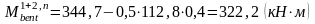
В данном случае для среднего пролета расчетный граневый момент принимается равным .

5.6. Расчёт прочности ригеля по сечениям, нормальным к продольной оси

5.6.1. Характеристики прочности бетона и арматуры.

Бетон тяжелый, класса В-25; расчетное сопротивление при сжатии R_b=14,5 МПа ; коэффициент условия работы бетона _b1=0,9; модуль упругости Е_b=30000 МПа.

Арматура продольная и поперечная класса А400 с R_s=355 МПа, модуль упругости E_s=200000 МПа.

5.6.2. Определение высоты сечения ригеля.

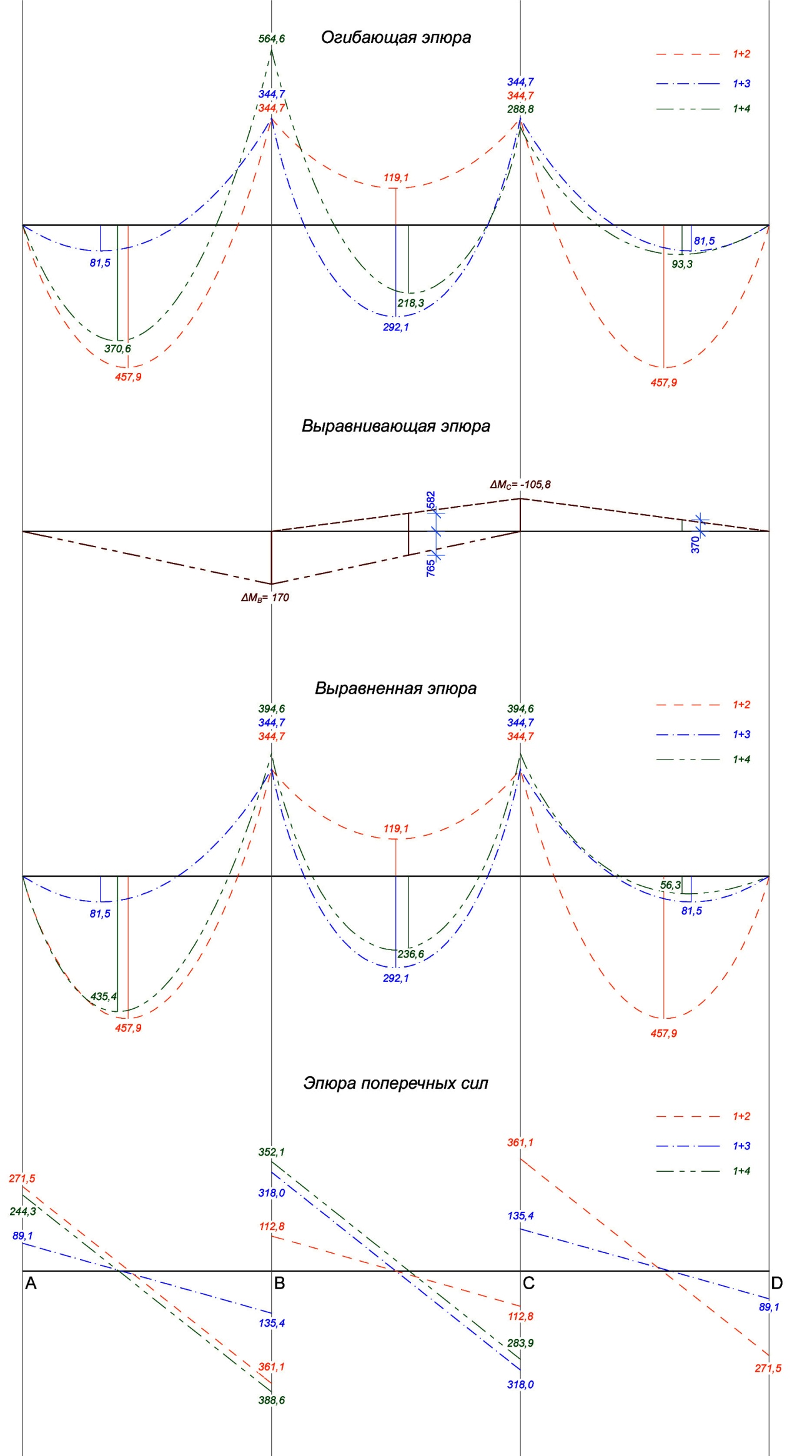
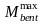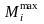Проверяем высоту сечения ригеля по наибольшему граневому моменту при относительной высоте сжатой зоны бетона ξ=0,4. Принятое сечение следует затем проверить по пролетному моменту (если он больше опорного ) так, чтобы соблюдалось условие: ξ<ξ_R.

.

.

Полная высота сечения принимается из условия h=h₀+a=70+5=75 см.

Конструктивно принимаем h=80 см, b=0,3h≈25 см, тогда h₀=80-5=75 см,