4.4.2. Ввод ограничений и граничных условий

1. Запускаем команду Поиск решения (см.приложение);

(Дополнение от Базыкина Я.В. студента гр.5Б11:

Если команда Поиск решении, во вкладке Данные отсутствует, её необходимо активировать, для этого:

1. Перейти в Файл -> Параметры.

2. Затем, в панели Надстройки, внизу, напротив Управление – выставить значение Надстройки Excel и нажать кнопку Перейти.

3. В открывшемся окне, поставить галочку напротив Поиск решений и нажать ОК.

4. Теперь команда Поиск решений активна и находится во вкладке Данные, в подменю Анализ.)

2. Назначаем целевую функцию:

1. Курсор в окно Установить целевую ячейку;

2. Ввести в ней адрес своей целевой ячейки: $F$11;

3. Ввести направление целевой функции: установить флажок в поле Равной минимальному значению.

2. Вводим адреса искомых переменных:

   1. Курсор в поле Изменяя ячейки;

   2. Ввести адреса матрицы независимых переменных: $C$16:$G$20.

3. Вводим ограничения:

   1. Курсор на кнопку Добавить;

   2. В диалоговом окне Добавление ограничения (рис.4.5) в поле Ссылка на ячейку ввести адреса $В$16:$B$20;

   3. Курсор на стрелку; из появившихся в меню знаков, выделить курсором знак =;

   4. В поле Ограничение ввести адреса $В$5:$B$9;

   5. Курсор на кнопку Добавить.

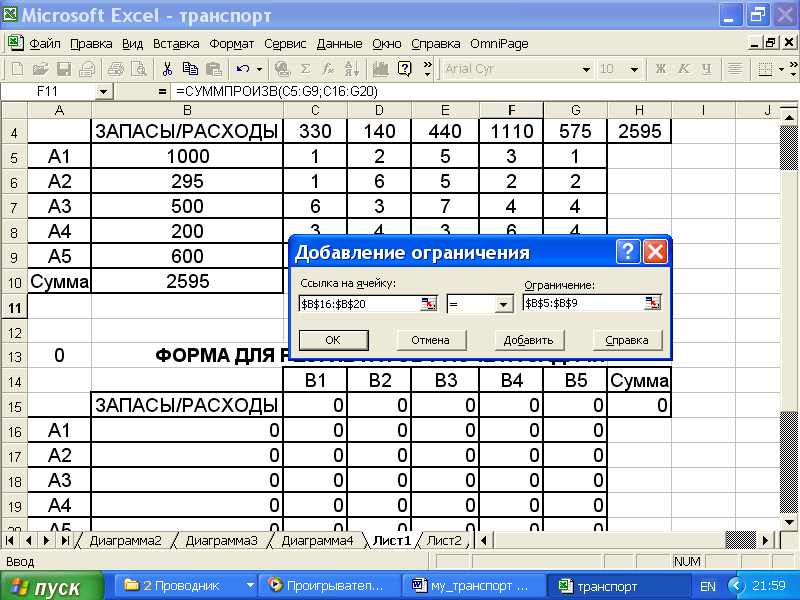
Рис.4.5.

На экране опять появится диалоговое окно Добавление ограничения с пустыми полями.

4.6. Аналогично ввести ограничения: $C$15:$G$15=$C$4:$G$4 и $C$16:$G$20>=0.

4.7. После ввода последнего ограничения вместо Добавить нажать ОК.

Если на этом этапе задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делается с помощью команд Изменить, Удалить в окне Поиск решения.

На этом ввод ограничений и граничных условий закончен и на экране появится диалоговое окно Поиск решения с введенными условиями (рис. 4.6).

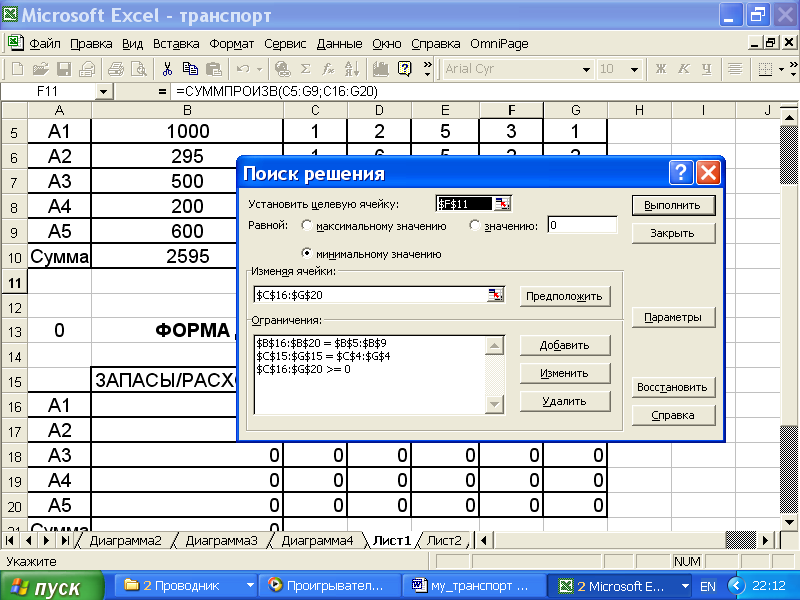
Рис.4.6.

4.4.3. Решение закрытой транспортной задачи

Решение задачи производится сразу же после ввода данных, целевой функции и ограничений, когда на экране находится диалоговое окно Поиск решения (рис. 4.6), путем выполнения следующих команд:

1. Нажать кнопку Параметры в окне Поиск решения;

2. Установить флажок в окне Линейная модель в появившемся диалоговом окне Параметры поиска решения (рис. 4.7);

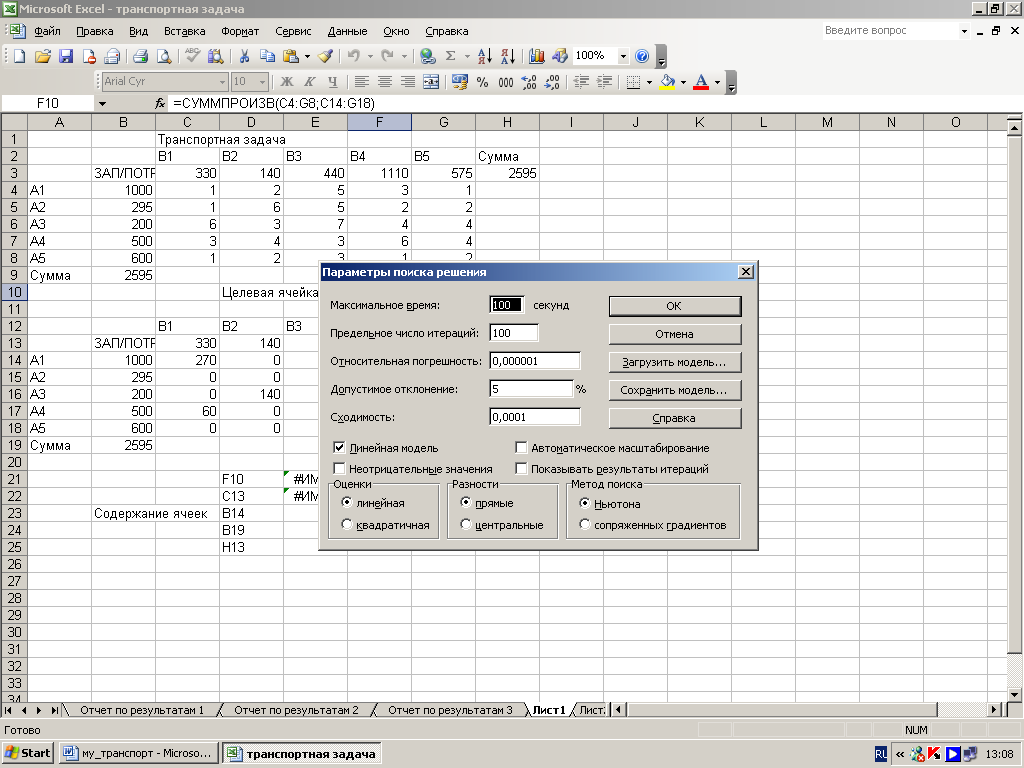
Рис.4.7.

3. Нажать кнопку ОК;

4. Нажать кнопку Выполнить в диалоговом окне Поиск решения.

На экране появится диалоговое окно Результаты поиска решения (рис.3.9 приложения).

В этом окне выводится информация о найденном решении. Одновременно результат оптимального решения задачи ( объемы перевозок из пп.А в пп.В) автоматически записывается в ячейки C16:G20, а значение целевой функции в ячейку F11 (рис.4.8).

5. Сохранить результат оптимального решения, выбрав требуемый тип отчета (см. с.12).

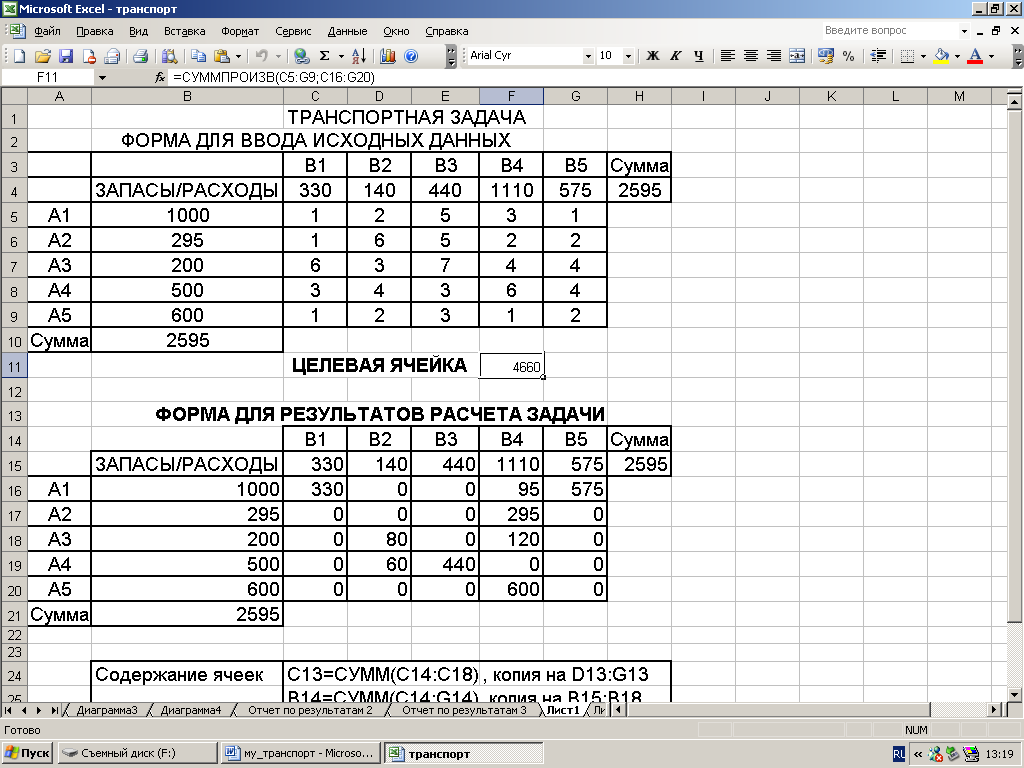
Рис.4.8.

В том случае, когда решение не найдено (рис.3.10-3.11), необходимо проверить ограничения и совместность условий.

5. Исследовать влияние изменения тарифов на распределение объемов перевозок и величину целевой функции.

6. Исследовать влияние изменения запасов топлива на распределение объемов перевозок и величину целевой функции.

7. Исследовать влияние изменения расходов топлива на распределение объемов перевозок и величину целевой функции.

8. Провести анализ полученных результатов с помощью отчетов Excel.