Порядок выполнения лабораторной работы (закрытая транспортная задача)
4.1. Выполнить постановку задачи
4.2. Описать математическую модель транспортной задачи.
4.4. Решить закрытую транспортную задачу симплекс-методом при помощи табличного процессора (ТП) Microsoft Excel.
4.4.1. Ввод данных для решения закрытой транспортной задачи
1. Для закрытой транспортной задачи
создаем форму для ввода условий в виде
таблицы. Количество строк и столбцов
этой формы должно соответствовать
количеству запасов и расходов топлива.
Вводим при помощи клавиатуры в ячейки
В5 – В9 коэффициенты
;
в ячейки С4 – G4
– коэффициенты
;
в ячейки C5 – G9
– коэффициенты
.
Изменение исходных данных можно
осуществлять только в этой форме
(рис. 4.1).
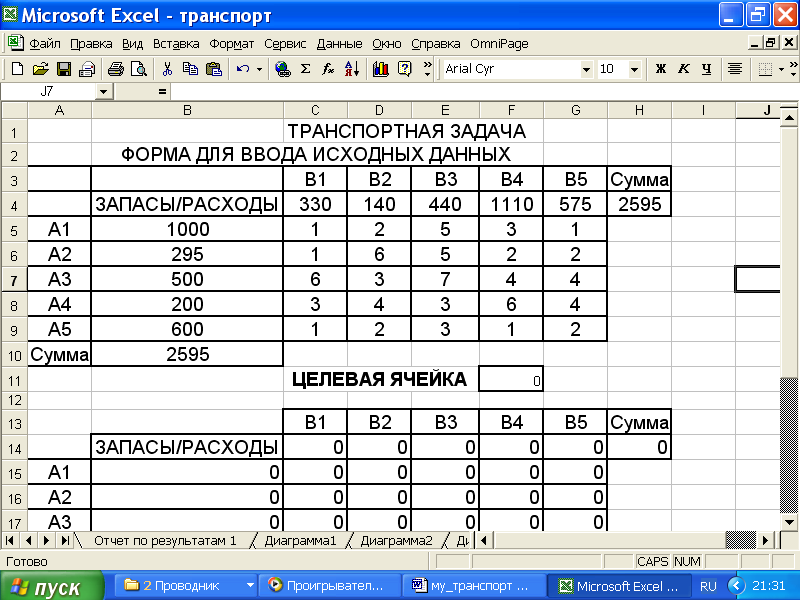
Рис.4.1. Форма для ввода условий задачи
Вводим зависимости из созданной математической модели. Для этого на том же листе создается аналогичная форма, содержимое которой отличается от содержимого формы для ввода данных (рис.4.2).
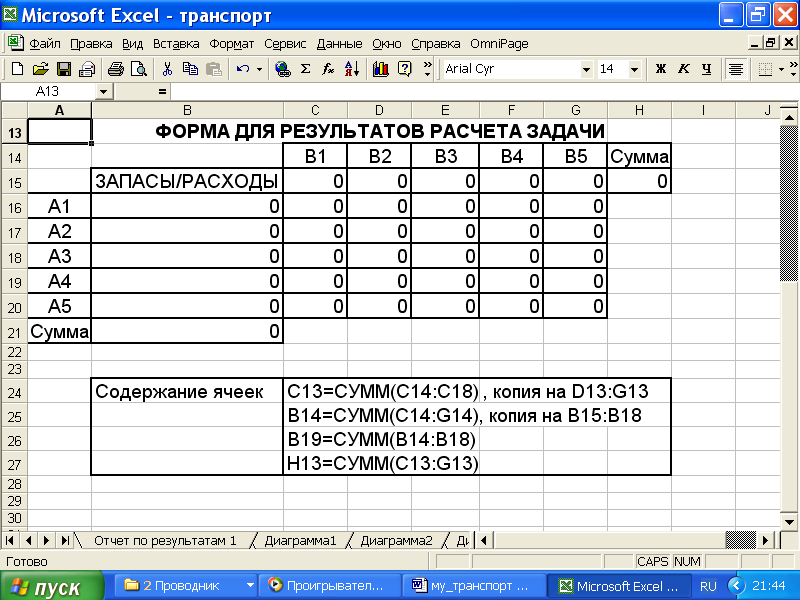
Рис.4.2. Форма для ввода зависимостей из математической модели
Ячейки С16 – G20 являются адресом матрицы независимых переменных, при заполнении они должны быть равными нулю. Ячейки C15 – G15 должны содержать действия, в результате которых выполняется ограничение (2). Ячейка С15 является суммой значений ячеек С16 – С20. Ее заполнение осуществляем при помощи Мастера функций (см.приложение).
2.1. Курсором выделить заполняемую ячейку С15;
2.2. Запустить Мастер функций и в диалоговом окне Мастер функций – шаг 1 из 2 курсором выбрать в окне Категория категорию Математические, а в окне Функции – СУММ;
2.3. Нажать кнопку ОК;
2.4. В диалоговом окне Аргументы функции в поле Число 1 ввести массив С16:С20. Справа от знака равенства появятся численные значения этого массива, а внизу окна – результат суммирования (рис.4.3);
Курсором нажать кнопку OK.
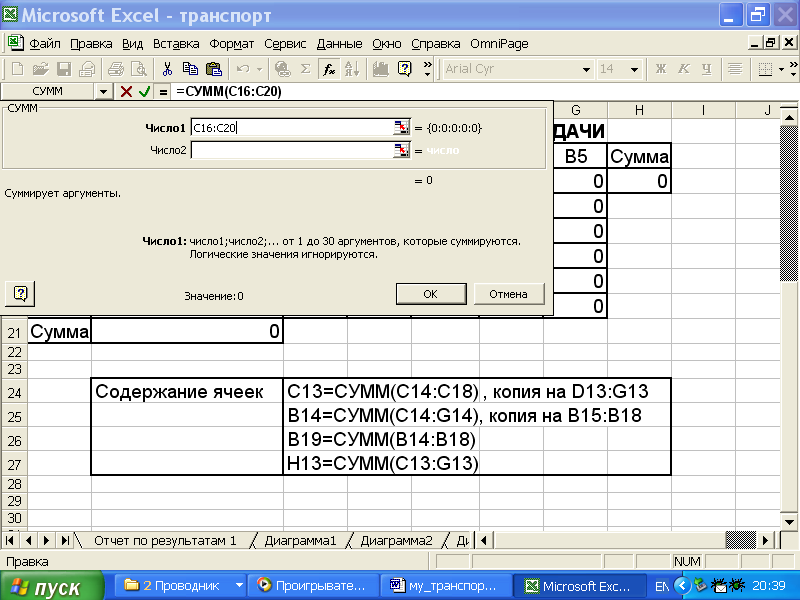
Рис.4.3.
Аналогичные действия выполняются при заполнении ячеек D15, E15, F15 и G15, которые являются суммами соответствующих столбцов.
Ячейки В16 – В20 должны содержать действия, в результате которых выполняется условие (3). Рассмотрим принцип заполнения ячейки В16, остальные ячейки этого столбца заполняются аналогично.
2.6. Выделить курсором ячейку В16;
2.7. Выполнить операции по пп. 2.2 – 2.3;
2.8. В поле Число 1 ввести массив C16:G16;
2.9. Курсором нажать кнопку OK .
Ячейка Н15 является суммой ячеек с С15 по G15, а ячейка В21 – суммой ячеек с В16 по В20. Их заполнение осуществляется по уже известному алгоритму.
3. Ввести зависимость для целевой функции, выполнив следующую последовательность операций:
Курсором выделить ячейку для целевой функции: например F10;
Запустить Мастер функций;
В диалоговом окне Мастер функций – шаг 1 из 2 выбрать в окне Категория категорию Математические, а в окне Функции – СУММПРОИЗВ;
Нажать кнопку ОК;
3.5. В появившемся диалоговом окне СУММПРОИЗВ в поле массив 1 ввести адреса матрицы коэффициентов целевой функции С5:G9, а в поле массив 2 ввести адреса матрицы независимых переменных C16:G20 (рис.4.4);
Курсором нажать кнопку OK.
На этом ввод данных в таблицы (рис. 4.1, рис. 4.2) закончен.
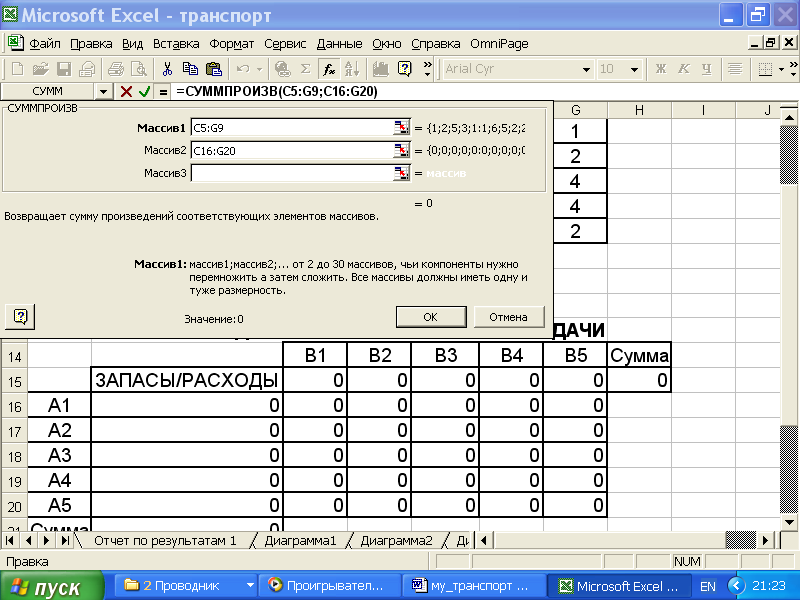
Рис.4.4.