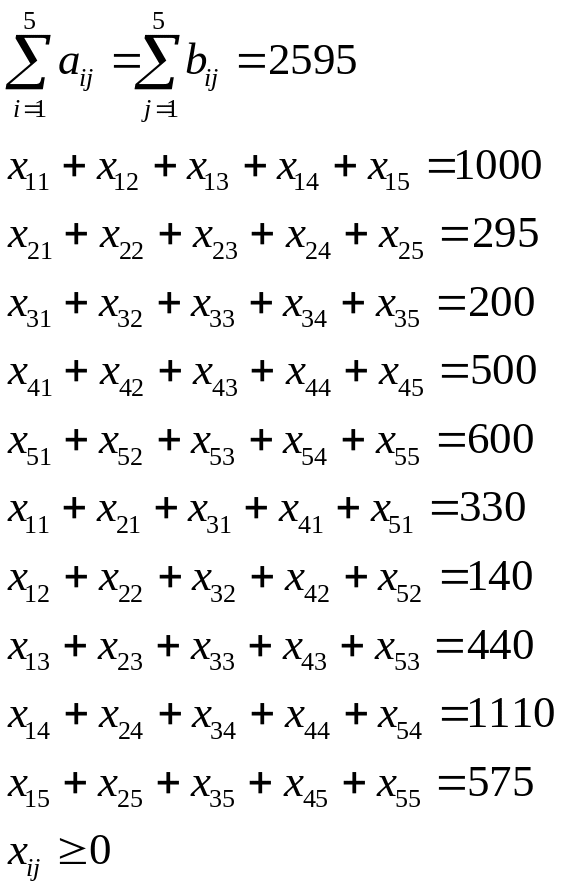- •Введение
- •Цель работы
- •Основные теоретические сведеНия
- •2.1. Общая формулировка транспортной задачи
- •2.2. Математическая постановка транспортной задачи
- •3. Пример транспортной задачи
- •Исходные данные
- •Порядок выполнения лабораторной работы (закрытая транспортная задача)
- •4.4.1. Ввод данных для решения закрытой транспортной задачи
- •4.4.2. Ввод ограничений и граничных условий
- •4.4.3. Решение закрытой транспортной задачи
- •Требования к содержанию отчета
- •Контрольные вопросы
- •Литература
- •Приложение 1 решение задач линейного программирования с помощью excel
- •Приложение 2 Открытая транспортная задача на избыток
- •Приложение 3 Варианты заданий к лабораторной работе
Введение
Лабораторная работа “Транспортная задача” предназначена для закрепления теоретических знаний, полученных студентами направления 140100 “ Теплоэнергетика“ при изучении методов линейного математического программирования.
Цель работы
Решить транспортную задачу при помощи табличного процессора (ТП) Microsoft Excel. Исследовать, как влияют на целевую функцию изменение тарифов перевозок и запасов угля.
Основные теоретические сведеНия
2.1. Общая формулировка транспортной задачи
Найти оптимальный план перевозок некоторого однородного груза из m пунктов отправления А1, А2,…, Аm в n пунктов назначения В1, В2,…, Вn. В качестве критерия оптимальности принять минимум суммарной стоимости перевозок всего груза.
Требуется так организовать перевозку угля, чтобы:
удовлетворить все заявки электростанций;
вывезти все запасы угля с месторождений;
3) суммарная стоимость всех перевозок топлива была бы наименьшей.
Введем следующие обозначения:
![]() - тарифы перевозки единицы груза из i-го
пункта отправления в j-й
пункт назначения;
- тарифы перевозки единицы груза из i-го
пункта отправления в j-й
пункт назначения;
![]() - запасы груза в i-м пункте
отправления;
- запасы груза в i-м пункте
отправления;
![]() - потребности в грузе в j-том
пункте назначения;
- потребности в грузе в j-том
пункте назначения;
![]() - планируемое количество единиц груза,
перевозимого из i-го пункта
отправления в j-й пункт
назначения.
- планируемое количество единиц груза,
перевозимого из i-го пункта
отправления в j-й пункт
назначения.
2.2. Математическая постановка транспортной задачи
Найти минимум
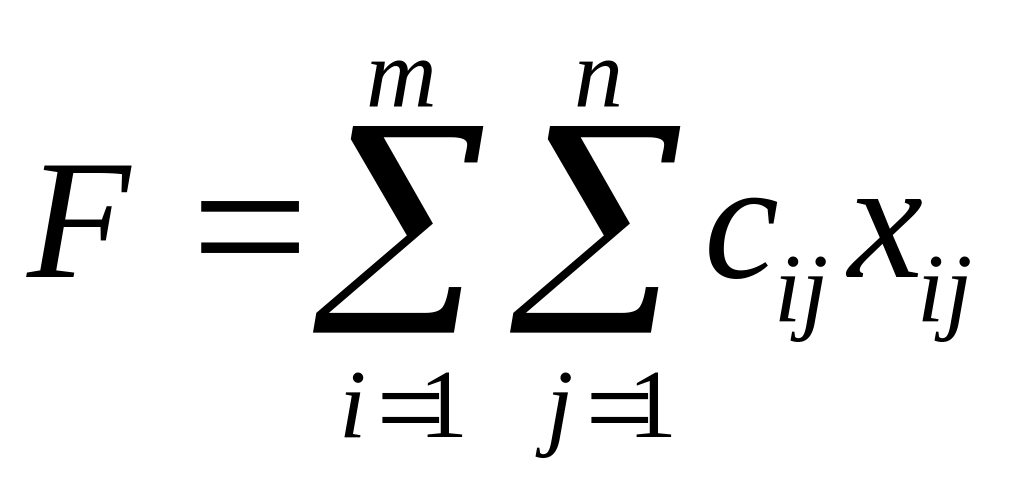 (1)
(1)
при условиях
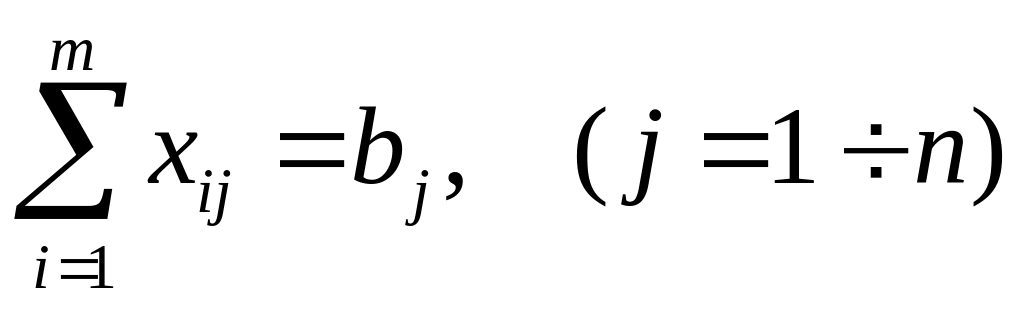 ;
(2)
;
(2)
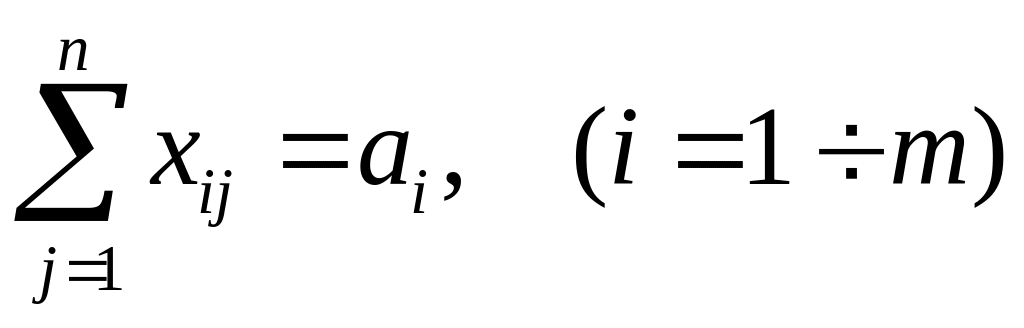 ;
(3)
;
(3)
![]() .
(4)
.
(4)
Всякое неотрицательное решение систем
линейных уравнений (2) и (3), определяемое
матрицей
![]() ,
называется планом транспортной
задачи.
,
называется планом транспортной
задачи.
План, при котором функция (1) принимает свое минимальное значение, называется оптимальным планом транспортной задачи.
3. Пример транспортной задачи
3.1. Постановка
Имеется 5 месторождений каменного угля
![]() с
запасами топлива
с
запасами топлива
![]() и 5 электростанций
и 5 электростанций
![]() ,
годовой расход топлива которых составляет
,
годовой расход топлива которых составляет
![]() ,
соответственно. Стоимость перевозки
единицы топлива
,
соответственно. Стоимость перевозки
единицы топлива
![]() от i-го месторождения к
j-той станции (в таблице
находится на пересечении соответствующих
строк и столбцов) и значения запасов
и расходов
заданы
в таблице 1.
от i-го месторождения к
j-той станции (в таблице
находится на пересечении соответствующих
строк и столбцов) и значения запасов
и расходов
заданы
в таблице 1.
Исходные данные
Таблица 1
|
Электро-станции |
В1 |
В2 |
В3 |
В4 |
В5 |
Всего |
Месторожде-ния |
Запасы / расходы |
b1=330 |
b2=140 |
b3=440 |
b4=1110 |
b5=575 |
2595 |
А1 |
а1=1000 |
1 |
2 |
5 |
3 |
1 |
|
А2 |
а2=295 |
1 |
6 |
5 |
2 |
2 |
|
А3 |
а3=200 |
6 |
3 |
7 |
4 |
4 |
|
А4 |
а4=500 |
3 |
4 |
3 |
6 |
4 |
|
А5 |
а5=600 |
1 |
2 |
3 |
1 |
2 |
|
всего |
2595 |
|
|
|
|
|
|
3.2. Математическая запись
План перевозок |
Матрица тарифов |
|
|
|
|
Целевая функция |
||
|
||
Ограничения |
||
|
(8)
|
|

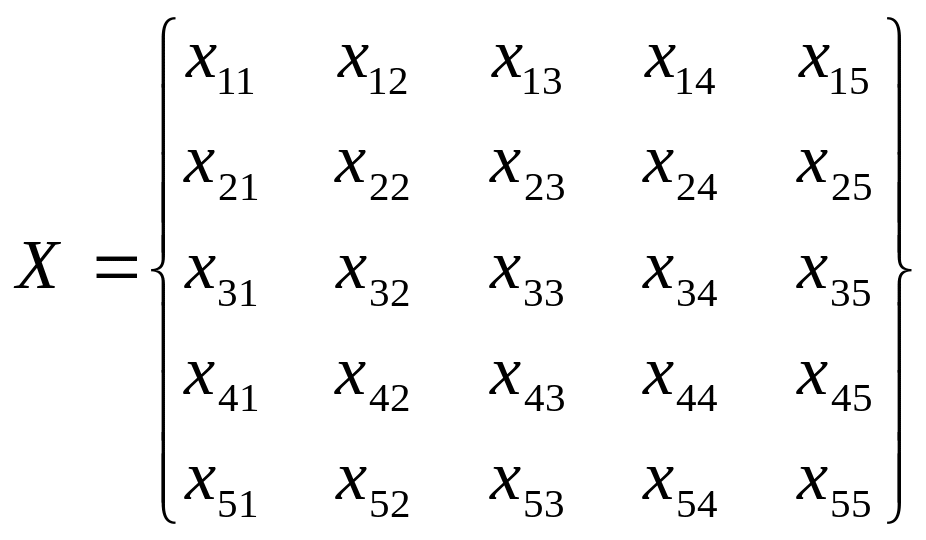 (5)
(5)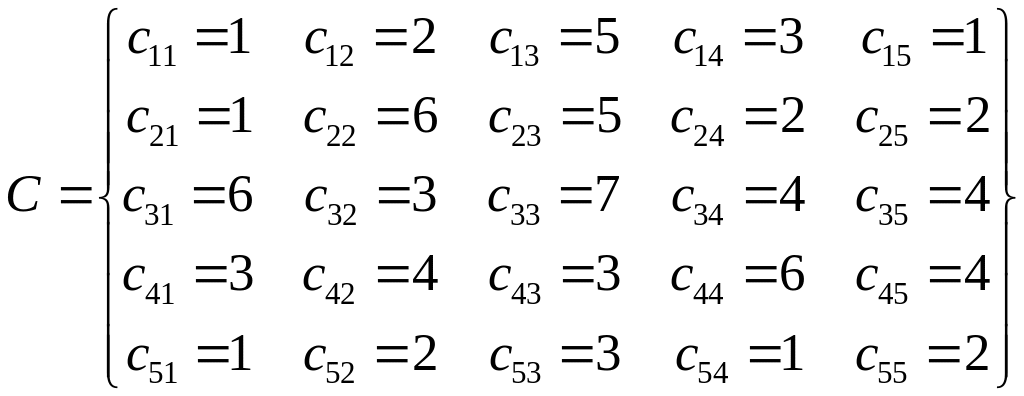 (6)
(6)