Целые неотрицательные числа

Задание 12. Докажите методом математической индукции, что для любого натурального числа п справедливо равенство.

Пример.

Решение. 1) Докажем, что равенство верно при п = 1. При п = 1 сумма представляется одним слагаемым, равным . Значение выражения при п = 1 также равно . Значит, при п = 1 равенство верно.

2) Предположим, что равенство верно для n=k>1, т.е. .

Докажем, что равенство верно и для n=k + 1, т.е. .

Действительно, =

, что и требовалось доказать.

Вывод: т.к. равенство верно для п = 1, и из предположения, что равенство верно для n=k>1, следует, что равенство верно для n=k + 1, то данное равенство верно для любого натурального числа п.

Варианты.

1. 1 + 2 + 3 + ... + п = ;

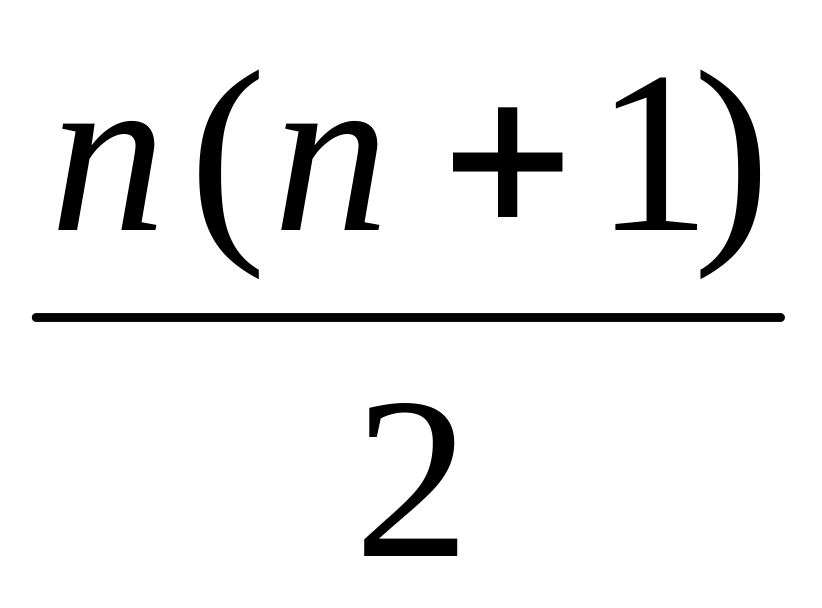2. 1² + 2² + 3² + ... + п² = ;

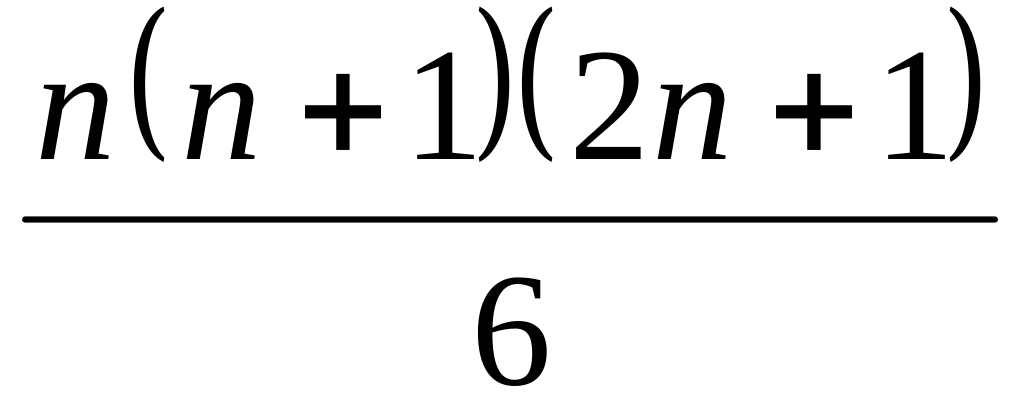3. 1² + 3² + 5² + ... + (2п – 1)² = ;

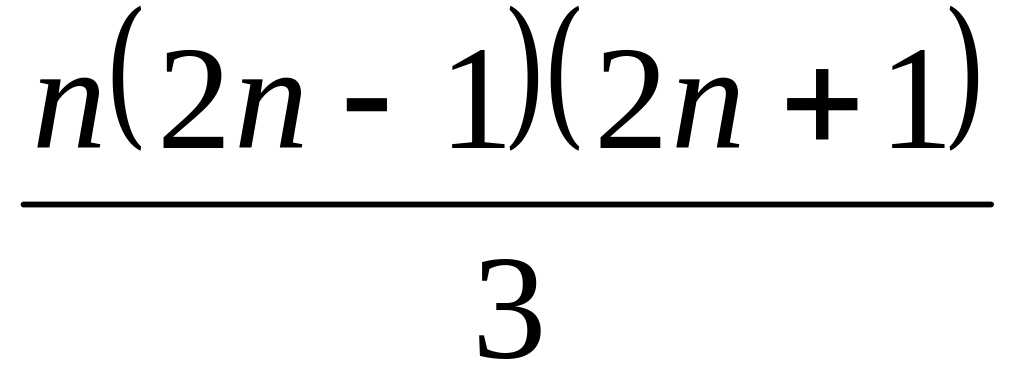4. 1·4 +2·7 + ... + п(3п + 1) = п(п + 1)²;

5. 1·2 +2·3 + ... + п(п + 1) = ;

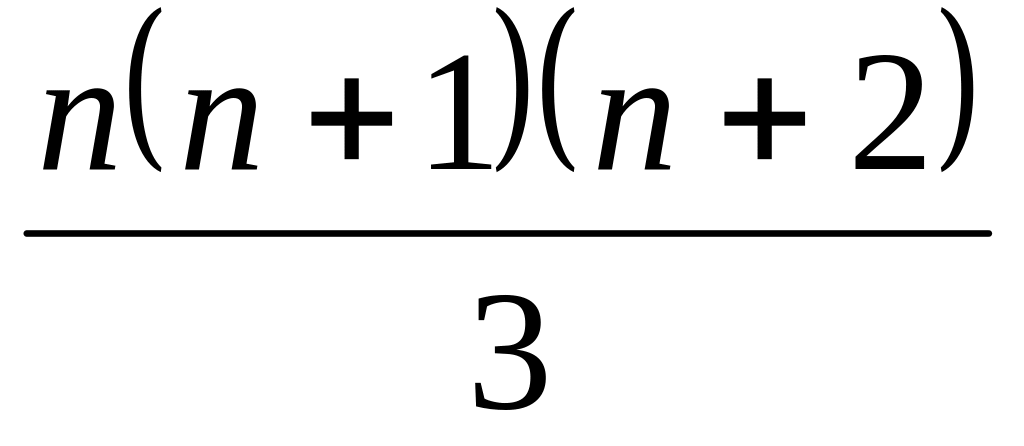6. 1 + 3 + 5 + ... + (2п – 1) = п²;

7. ;

8. ;

9. ;

10. .

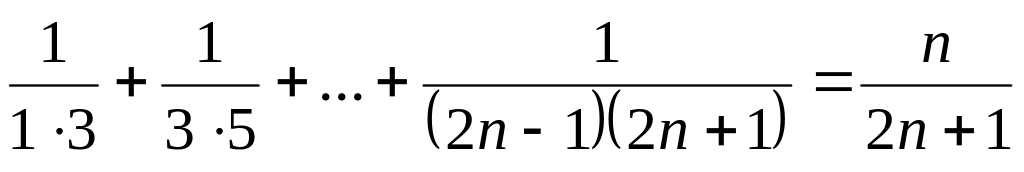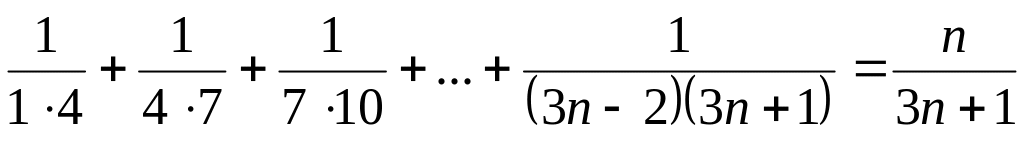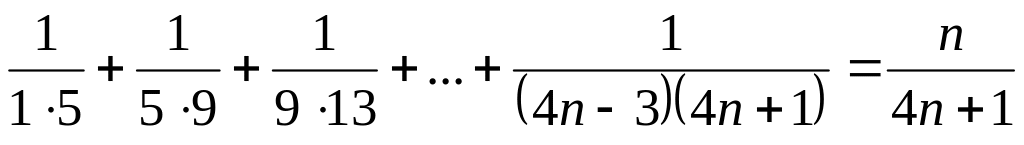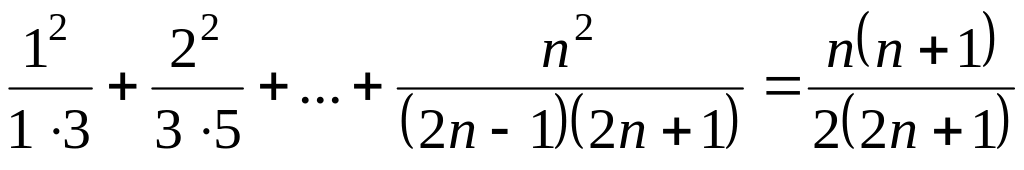Задание 13. Используя теоретико-множественный и аксиоматический подходы к построению множества целых неотрицательных чисел, докажите истинность утверждений.

Варианты.

1. 2 < 5; 2 + 5 = 7; 7 – 5 = 2; 5 · 2 = 10; 10 : 2 = 5;

2. 3 < 4; 3 + 4 = 7; 7 – 3 = 4; 3 · 4 = 12; 12 : 3 = 4;

3. 2 < 6; 2 + 6 = 8; 8 – 2 = 6; 2 · 6 = 12; 12 : 2 = 6;

4. 5 > 3; 5 + 3 = 8; 8 – 5 = 3; 5 · 3 = 15; 15 : 3 = 5;

5. 4 < 6; 4 + 6 = 10; 10 – 4 = 6; 4 · 2 = 8; 8 : 2 = 4;

6. 6 > 3; 6 + 3 = 9; 9 – 6 = 3; 6 · 3 = 18; 18 : 3 = 6;

7. 2 < 7; 2 + 7 = 9; 9 – 7 = 2; 7 · 2 = 14; 14 : 2 = 7;

8. 3 < 7; 3 + 7 = 10; 10 – 3 = 7; 3 · 7 = 21; 21 : 7 = 3;

9. 2 < 8; 2 + 8 = 10; 10 – 8 = 2; 8 · 2 = 16; 16 : 2 = 8;

10. 8 > 3; 8 + 3 = 11; 11 – 8 = 3; 4 · 3 = 12; 12 : 4 = 3.

Системы счисления

Задание 14. Запишите числа а и b в системе счисления с основанием q и разделите большее на меньшее с остатком.

Пример. а = 7356₈, b = 23₄, q = 5.

Решение. Переведем числа 7356₈ и 23₄ в пятеричную систему счисления. Для этого мы можем воспользоваться способом деления или способом умножения.

Способ деления.

Для перевода числа 7356₈ в пятеричную систему счисления выполним последовательное деление этого числа и получаемых неполных частных в восьмеричной системе счисления на новое основание системы счисления 5.

_ 7356₈ __5 __

5___ _1374 __5_

_ 23 12 _230 __5_

17_ _17 17 _36 _5_

_45 17 _40 36 _6 __5_

43  36  5 

_26  

24



Мы разделили 7356₈ на 5 в восьмеричной системе счисления, получив неполное частное 1374₈ и остаток 2; затем найденное неполное частное 1374 разделили в восьмеричной системе счисления снова на 5, получив неполное частное 230₈ и остаток 4; далее разделили 230₈ на 5, получив 36₈ и в остатке 2, потом 36₈ разделили на 5, получив 6₈ и остаток 0; наконец, разделили 6₈ на 5, получив неполное частное 1 и остаток 1, на чем мы и закончили деление, т.к. неполное частное оказалось меньше 5. Последовательность остатков и последнее неполное частное, взятые в обратном порядке, дает последовательность цифр для записи числа 7356₈ в пятеричной системе счисления: 7356₈ = 110242₅.

А налогично найдем запись числа 23 в пятеричной системе счисления. Так как последовательное деление надо проводить в четверичной системе счисления, то следует число 5 (поскольку оно больше 4) записать в четверичной системе счисления: 5 = 11₄.

Имеем: 23 11

22 

 Таким образом, 23₄ = 21₅

Способ умножения.

7356₈ = ((7·8 +3) · 8 +5) · 8 + 6 = (((12·13+3) · 13 +10) · 13 +11)₅ =







12₅ 214₅ 3402₅

+

13₅ _13₅ __13₅

+

+

41 1202 21211

12_ 214_ 3402_

+

+

+

211 3342 110231

__3 __10 ___11

214₅ 3402₅ 110242₅

Представим число 23₄ в пятеричной системе счисления:23₄ = (2 · 4 + 3)₅ = 13₅ +3₅ = 21₅.

Теперь разделим большее число 110242₅ на меньшее 21₅, не указывая в промежуточных вычислениях основание системы счисления 5.



_110242₅ _21₅ Проверка: 2342₅

+

_42_ 2342₅ __21₅

_132 2342

113 10234_

+

_144 110232

134 ____10

_102 110242₅

_42

10₅ Ответ: 110242₅ = 21₅ · 2342₅ + 10₅.

Варианты.

1. а =3124₉, b =32₅, q =7;

2. а =4817₉, b =54₆, q =7;

3. а =7834₉, b =244₅, q =7;

4. а =7211₈, b =232₄, q =5;

5. а =2345₇, b =221₃, q =6;

6. а =4110₇, b =17₈, q =9;

7. а =2343₅, b =65₇, q =4;

8. а =3471₈, b =201₅, q =6;

9. а =2413₅, b =44₉, q =7;

10. а =3451₆, b =301₄, q =5.