Соответствия

Задание 4. Между элементами множеств Х и Y задано соответствие R. Постройте граф соответствия R. Выясните, является ли оно взаимно однозначным отображением множества Х на множество Y?

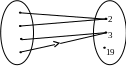
Пример. Х = {4, 15, 9, 8}, У = {2, 3, 19}, R: «число х делится на число у» (х  х, у  У). Выясните, является ли данное соответствие отображением.

Решение. Построим граф данного соответствия.

Х У

4

8

15

9

Видим, что каждому элементу из множества Х соответствует только один элемент из множества У. Следовательно, данное соответствие является отображением Х в У. Но его нельзя назвать отображением Х на У, поскольку не каждый элемент из множества У соответствует элементам множества Х. Так, число 19 не соответствует ни одному элементу множества Х.

Ответ: данное соответствие не является взаимно однозначным отображением множества Х на множество У; оно является отображением множества Х в множество У.

Варианты.

1. Х = {10, 18, 16}, Y= {3, 4, 5}, R: «х кратно у »;

2. Х = {1, -1, 2, -2, 3, -3}, Y= {1, 4, 9}, R: «квадрат числа х равен у »;

3. Х = {2, 3, 5, 7}, Y= {25, 9, 49, 4}, R: «квадрат числа х равен числу у»;

4. Х = {2, 3, 5, 7}, Y= {15, 28, 37}, R: «х – делитель у »;

5. Х = {8, 9, 12, 6}, Y= {11, 9, 15, 12, 17}, R: «х < у на 3»;

6. Х = {1, 2, 3, 4, 5, 6}, Y= {0, 1}, R: « у – остаток при делении х на 2»;

7. Х = {1, 2, 3, 4, 5}, Y= {0, 1, -1, 2, -2}, R: «х > у на 3»;

8. Х = {1, 3, 7, 4, 6}, Y= {1, 6, 8, 12, 14}, R: «х < у в два раза »;

9. Х = {3, 5, 7, 11}, Y= {15, 22, 28}, R: «х – делитель у »;

10. Х = {3 · 4, 10 - 3, 4 + 3, 0 : 5}, Y= {0, 7, 5, 12}, R: «значение выражения х равно у ».

Задание 5. Докажите, что множество натуральных чисел равномощно множеству А.

Пример. А – множество четных натуральных чисел.

Решение. N = {1, 2, 3, 4, 5,..., п,...}, А = {2, 4, 6, 8, 10,..., 2п,...}. Два множества Х и У называются равномощными, если существует взаимно однозначное соответствие множества Х на множество У. Поставим каждому элементу множества N элемент множества У: 1 → 2, 2 → 4, 3 → 6, ..., п → 2п,... Видим, что каждому элементу множества N соответствует только один элемент множества А. Кроме того, каждый элемент множества А соответствует ровно одному элементу множества N. Следовательно, установленное нами соответствие является взаимно однозначным, а значит, множество А равномощно множеству четных натуральных чисел.

Варианты.

1. А – множество нечетных натуральных чисел;

2. А – множество дробей вида 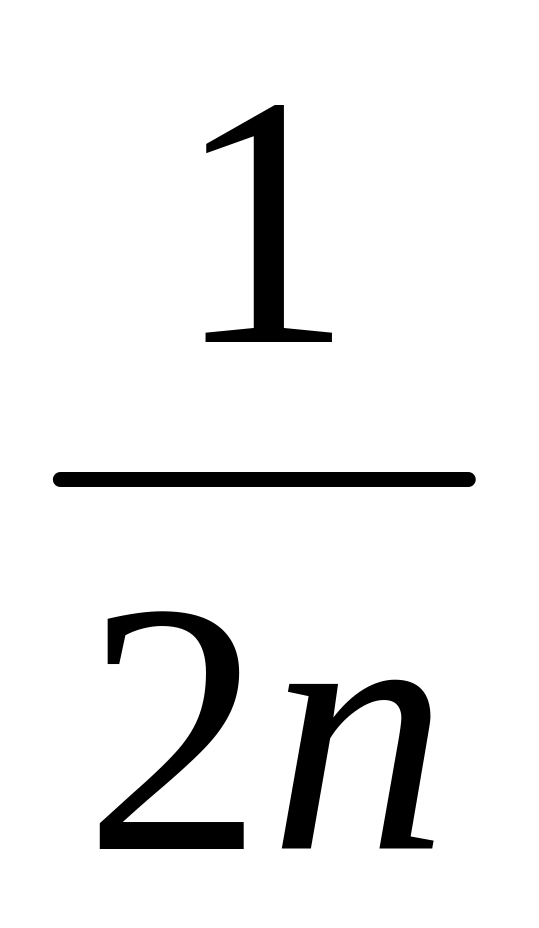, где п – натуральное число;

3. А – множество целых неотрицательных чисел;

4. А – множество квадратов натуральных чисел;

5. А – множество чисел вида 3^п;

6. А – множество натуральных чисел, кратных 5;

7. А – множество кубов натуральных чисел;

8. А – множество дробей вида , где п – натуральное число;

9. А – множество натуральных чисел, кратных 7;

10. А – множество натуральных чисел, больших 5.