МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ГЛАЗОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ

им. В.Г.Короленко

Контрольные работы по математике (для студентов факультета ПиМно)

Глазов 2002

Контрольные работы по математике

Составители: ст. преподаватель кафедры МНО, Г.В. Керова

ст. преподаватель кафедры МНО, Г.Ф. Микрюкова

Рецензент: канд. физ.-мат. наук, доцент кафедры математического анализа

В.В. Маев

Данное пособие содержит задания контрольных работ по математике, предусмотренных учебным планом заочного отделения по специальности “Педагогика и методика начального образования”.

Большинство заданий сопровождается примером с подробным решением. Пособие может быть использовано студентами факультета ПиМНО для самостоятельной работы при подготовке к контрольным работам, зачетам и экзаменам.

Множества и операции над ними Задание 1. Изобразите на числовой прямой множества а и в, их дополнения и определите

Пример. A = [-3; 2), В = [0; 4)

Решение. Изобразим данные множества на координатной прямой (рис.1)

B

A

-3 0 2 4

Рис. 1

Известно, что пересечением множеств A и В называется множество, содержащее те и только те элементы, которые принадлежат множеству A и множеству В. Числа, принадлежащие одновременно обоим множествам, содержатся в промежутке [0; 2). Следовательно, A  В = [0; 2).

Объединением множеств A и В называется множество, содержащее те и только те элементы, которые принадлежат множеству A или множеству В. В нашей задаче числа, принадлежащие хотя бы одному из указанных множеств, образуют промежуток [-3; 4). Следовательно, A  В = [-3; 4).

Разностью множеств A и В называется множество, содержащее те и только те элементы, которые принадлежат множеству A и не принадлежат множеству В. Числа, принадлежащие множеству A и не принадлежащие множеству В, образуют промежуток [-3; 0).

Обратим внимание на то, что число 0 принадлежит множеству В, поэтому оно не входит в разность множеств A и В.

В том случае, когда В  A, разность множеств A и В называют дополнением множества В до множества A и обозначают В_A. Если В - подмножество универсального множества, то дополнение множества В до универсального множества обозначают В.

В качестве универсального множества возьмем множество всех действительных чисел. Тогда A =(-∞; -3)  2; +∞). Изобразим множества A, В и A на числовой прямой (рис.2) и, пользуясь определением пересечения множеств, найдем A  В.

B

A

Рис. 2

-3 0 2 4 x

A  В = [2; 4).

Изобразим множества A, В и В = (-∞; 0)  [4; +∞) на числовой прямой (рис.3)

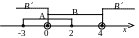
Рис. 3

Найдем A  В и В \ A, пользуясь определением объединения и разности множеств.

A  В = (-∞; 2)  [4; +∞)

В \ A = (-∞; -3)  [4 ; +∞).

Варианты.

1. А=(0; 7], B=[7; 9);

2. А=(2; 8), B=[7; 11];

3. А=(1; 9), B=[5; 7];

4. А=(0; 2), B=[2; 5];

5. А=(1; 7], B=(5; 8);

6. А=(2; 7], B=(7; 10];

7. А=(-5; 1], B=(-2; 5];

8. А=(2; 7], B=[3; 4);

9. А=(-5; 3], B=(1; 4];

10. А=(1; 9), B=[-5; 7].