
Лабораторная работа №5
“Программирование с использованием динамических массивов и функций”
Цель работы: освоение методов составления алгоритмов и написания программ с использованием функций для ввода массивов, вывода их на печать, выполнения их обработки и преобразования, а также получение навыков работы с динамической памятью и указателями.
1. Теоретическая часть
1.1. Описание динамических массивов в языке программирования C++.
Для того, чтобы работать с массивом как с динамическим, выделяя под него память в процессе работы программы, массив должен быть объявлен в разделе описания переменных как указатель на соответствующий тип:
тип *имя_массива;
где:
тип – указание на любой стандартный или нестандартный тип, которому будут принадлежать элементы массива;
имя_массива – идентификатор массива;
Выделение памяти под массив в программе возможно с помощью оператора new:
имя_массива = new тип[N];
где:
N – количество элементов в массиве, целое число.
Обращение к элементам динамического массива в программе происходит по индексам: D[i]
или через указательное обращение: *(D+i).
После того, как работа с массивом в программе завершена, необходимо с помощью оператора delete обязательно освободить память, выделенную под массив оператором new:
delete[] имя_массива.
Поскольку элементы двумерных массивов располагаются в памяти непосредственно друг за другом, работу с ними, используя динамическое выделение памяти, можно осуществлять аналогичным образом:
тип *имя_матрицы;
имя_матрицы = new тип[NxM];
где:
N – количество строк в матрице, целое число.
M – количество столбцов матрицы, целое число.
Обращение к элементам динамического массива в этом случае происходит только через указательное обращение:
*(A+i*M+j).
Работа с динамическими двумерными массивами может осуществляться в языке С++ и другим способом:
тип **имя_матрицы;
имя_матрицы = new тип*[N];
for(i=0;i<N;i++)
имя_матрицы[i] = new тип[M];
где:
N – количество строк в матрице, целое число.
M – количество столбцов матрицы, целое число.
Обращение к элементам динамического массива в этом случае происходит обычным образом по двум индексам: A[i][j].
После того, как работа с массивом в программе завершена, необходимо, как и при работе с одномерными динамическими массивами, с помощью оператора delete обязательно освободить память, выделенную под массив оператором new:
for(i=0;i<N;i++)
delete[]имя_матрицы[i];
delete[]имя_матрицы;
1.2 Описание функций в языке программирования C++.
Использование функций в программе включает 2 этапа: описание, вызов.
Описание функции:
тип имя_функции(тип1 арг1, тип2 арг2,…тип n арг n);
{ описание;
…
операторы;
…
}
где: тип – указывает тип возвращаемого результата, если он отсутствует, то подразумевается целый (int). Если функция не возвращает значение, то ее тип void.
имя_функции – идентификатор для обозначения функции;
тип i аргi – список формальных параметров функции с указанием их типов (иногда они могут отсутствовать, тогда скобки пустые);
описание – описание внутренних или локальных объектов функции;
операторы – выполняемая часть функции.
Вызов функции.
Если функция описана как void и не возвращает значений, то ее вызов является самостоятельным оператором:
имя_функции (список фактических параметров)
Список фактических параметров должен четко соответствовать списку формальных параметров по количеству, порядку следования и типу.
Если в описании функции указан тип или он отсутствует, то вызов функции не является самостоятельным оператором, а должен записываться внутри какого-либо другого оператора, например, оператора присваивания, условного оператора и др.:
b = имя_функции (список фактических параметров)
Если функция возвращает одно или несколько значений через свои аргументы, то при описании может быть указан любой тип, но чаще используют void, аргументы с возвращаемыми значениями должны быть описаны как указатели (тип *ptx,…), внутри описания функции такие аргументы должны использоваться как указатели *ptx = … , при вызове функции в качестве возвращаемого элемента записывается соответствующая переменная (ее адрес):
имя (…,&x,…)
Если в качестве аргумента функции используется одномерный массив, возможны несколько вариантов его использования:
тип имя_функции(…,float x[], int n,…) – массив используется без указания размеров, а среди переменных должна быть переменная, указывающая на этот размер.
тип имя_функции(…,float *ptx, int n,…) – массив описывается в виде указателя на массив, длина массива – n элементов, элементы массива записываются через указатель. При вызове программы указывается имя массива и его размер.
тип имя_функции(…,float a[50],…) – передача массива фиксированной длины. В этом случае нельзя передавать массивы разной длины.
Если аргументом функции является двумерный массив, возможны также несколько вариантов:
тип имя_функции(…,float x[5][7],…) – двумерный массив записывается с указанием фиксированной размерности.
тип имя_функции(…,float x[][7],int m,…) – массив задается с фиксированным количеством столбцов. При этом способе есть возможность передачи массивов с разным количеством строк.
тип имя_функции(…,float *ptx,int n,int m,…) – массив задается в виде указателя на его начало, количество строк и столбцов задается отдельно. Элементы массива внутри функции записываются:
*(ptx + i*m + j)
1.3 Пример составления алгоритма и программы на языке C++ для обработки и преобразования двумерного массива.
Задание:
Дана матрица действительных чисел А(5х5). Найти Amin – минимальный элемент среди элементов, расположенных ниже главной диагонали, и Amax – максимальный элемент среди элементов, расположенных выше главной диагонали, Разделить элементы, расположенных ниже главной диагонали, на Amin, а выше главной диагонали – на Amax. Задание выполнить с помощью функций:
– ввода элементов матрицы случайным образом;
– вывода элементов матрицы на экран;
– нахождения Amin и Amax;
– преобразования матрицы.
Решение.
Постановка задачи.
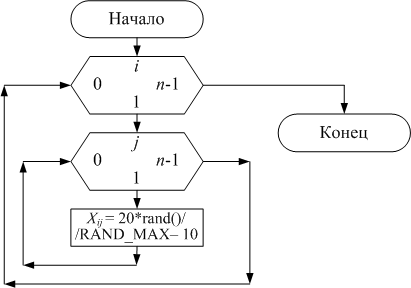
Для вода элементов матрицы организуем функцию void form_matr (float X[5][5], int n). Внутри нее выполним ввод элементов матрицы с помощью генератора случайных чисел rand(). Для обозначения размерности матрицы в функцию будем передавать переменную n.
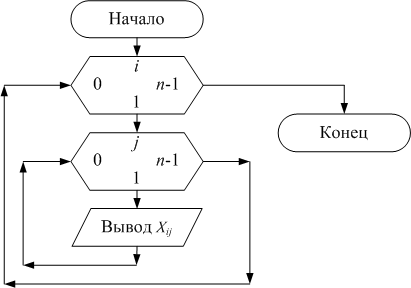
После формирования элементов матрицы выведем ее на экран, для чего организуем функцию void print_matr (float X[5][5], int n).
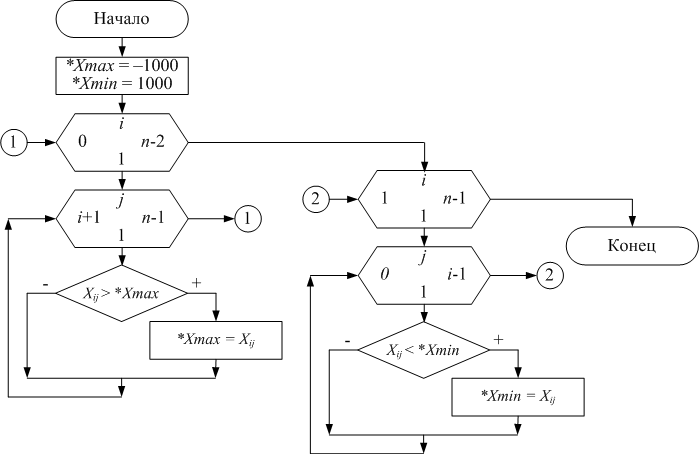
Для поиска максимального элемента среди элементов, расположенных выше главной диагонали и минимального элемента среди элементов, расположенных ниже главной диагонали организуем функцию void min_max (float X[5][5],int n,float *Xmin,float *Xmax). Данная функция возвращает в основную программу два результата: *Xmin и *Xmax, поэтому в списке формальных параметров они описаны как указатели.
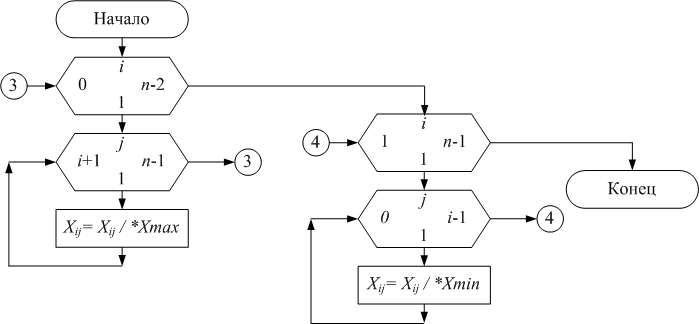
Для выполнения деления элементов матрицы в соответствии с заданием организуем функцию void change_matr(float X[5][5],int n,float Xmin,float Xmax).
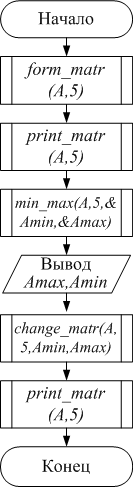
1.2.1 Блок схема:
void form_matr(float X[5][5],int n)
void min_max(float X[5][5],int n,float *Xmin,float *Xmax)
void print_matr(float X[5][5],int n)
void change_matr(float X[5][5],int n,float Xmin,float Xmax)
int main()
1.2.2 Текст программы на языке C++:
#include<stdio.h>
#include<stdlib.h>
#include<conio.h>
void form_matr(float X[5][5],int n)
{
int i,j;
for (i=0;i<n;i++)
for (j=0;j<n;j++)
X[i][j]=20.0*rand()/RAND_MAX-10;
}
void print_matr(float X[5][5],int n)
{
int i,j;
for (i=0;i<n;i++)
{ for (j=0;j<n;j++)
printf("%7.2f",X[i][j]);
printf("\n");
}
}
void min_max(float X[5][5],int n,float *Xmin,float *Xmax)
{
int i,j;
*Xmin=1000;
*Xmax=-1000;
for(i=0;i<n-1;i++)
for (j=i+1;j<n;j++)
if (X[i][j]>*Xmax) *Xmax=X[i][j];
for(i=1;i<n;i++)
for (j=0;j<i;j++)
if (X[i][j]<*Xmin) *Xmin=X[i][j];
}
void change_matr(float X[5][5],int n,float Xmin,float Xmax)
{
int i,j;
for(i=0;i<n-1;i++)
for (j=i+1;j<n;j++)
X[i][j]=X[i][j]/Xmax;
for(i=1;i<n;i++)
for (j=0;j<i;j++)
X[i][j]=X[i][j]/Xmin;
}
int main()
{
int i,j;
float A[5][5],Amin,Amax;
clrscr();
randomize();
printf(" Matrix A:\n");
form_matr(A,5);
print_matr(A,5);
min_max(A,5,&Amin,&Amax);
printf("\nMaximum vishe glavnoi diagonali: %.2f",Amax);
printf("\nMimimum nije glavnoi diagonali: %.2f",Amin);
printf("\n\n New matrix A:\n");
change_matr(A,5,Amin,Amax);
print_matr(A,5);
getch();
return 0;
}
1.2.3 Результаты работы программы:
Matrix A:
8.25 -7.28 -5.42 0.51 -4.77
5.30 5.65 5.37 9.92 -4.35
-5.76 0.34 7.84 6.87 4.43
5.18 -7.03 -9.93 8.71 -1.17
7.96 4.54 -5.69 -0.74 3.20
Maximum vishe glavnoi diagonali: 9.92
Mimimum nije glavnoi diagonali: -9.93
New matrix A:
8.25 -0.73 -0.55 0.05 -0.48
-0.53 5.65 0.54 1.00 -0.44
0.58 -0.03 7.84 0.69 0.45
-0.52 0.71 1.00 8.71 -0.12
-0.80 -0.46 0.57 0.07 3.20
