
Методика выполнения работы
1. Изучите теоретическую часть, проанализируйте приведенный пример 1. Оформите свои три задания по предыдущим лабораторным работам в виде функций. Организуйте меню с вызовом любой из них.
2. Проанализируйте приведенный в теоретической части пример 2. Создайте программу вычисления заданий по вариантам, приведенным в таблице 7.1.
Таблица 7.1 – Варианты заданий
Задание № .Функции |
|||
Вариант |
Задание |
Примечание |
|
1 |
Даны х. Составить программу вычисления значения выражения |
|
|
2 |
Дан x. Составить программу вычисления значения выражения |
|
|
3 |
Даны цены 10 товаров, которые увеличились на Р%. Используя функцию нахождения процента, найти их новые стоимости и общую стоимость |
||
4 |
Даны
а и b.
Используя функции нахождения min
и max
найти x=min(a,b),
y=max(a,b).
Вычислить значение выражения |
||
5 |
Даны
действительные числа а,b,c.
Вычислить значения выражения
|
||
6 |
В правильном треугольнике проведена средняя линия. Найти площадь образовавшейся трапеции, дважды используя функцию вычисления площади |
|
|
7 |
Для правильного треугольника со стороной а построены вписанная и описанная окружности. Найти площадь образовавшегося кольца, используя функцию вычисления площади круга S=πR2. Для нахождения радиусов окружностей воспользуйтесь формулами |
|
|
8 |
На товар дважды была сделана скидка – на p1, а затем на p2 процентов. Первоначальная стоимость товара составляла S рублей. Используя функцию вычисления стоимости товара с учетом скидки на P процентов, найти стоимость товара после двойной скидки. |
|
|
9 |
|
||
10 |
|
||
11 |
Даны
действительные числа s,
t.
Вычислить
|
||
12 |
Даны
действительные числа s,
t.
Вычислить
|
||
13 |
Даны
действительные числа а,b,c.
Вычислить
|
||
14 |
Сколькими способами можно отобрать команду в составе 5 человек из 8 кандидатов; из 10 кандидатов; из 11 кандидатов. |
Выбрать
k
человек из n
кандидатур можно С способами, где
|
|
15 |
Составить программу вычисления высот треугольника со сторонами ai,bi,ci (i=1,2,3,4) |
Высоты треугольника определяются по формулам: Ha=2S/ai ; Hb=2S/bi ; Hc=2S/ci, S=√p*(p-ai)*(p-bi)*(p-ci)
; |
|
16 |
Два спортсмена одновременно начинают движение из одной точки. Первый спортсмен начинает движение со скоростью 10 км/ч и равномерно за каждый следующий час увеличивает скорость на 1 км. Второй начинает движение со скоростью 9 км/ч и равномерно за каждый следующий час увеличивает скорость на 1,6 км/ч. Выяснить, какой спортсмен преодолеет больший путь через 1 час; через 4 часа, 7 часов. |
||
17 |
В партии, состоящей из k изделий, имеется L дефектных. Из партии выбирается для контроля R изделий. Найти вероятность того, что из R ровно S изделий будут дефектными. |
k=10; L=5; r=4; s=2. Вероятность определяется как:
|
|
18 |
Определить вероятность того, что в семье имеющей 6 детей не больше 4 девочек. |
Веpоятность
pождения девочки p=0.5, мальчика q=1-p
Веpоятность того, что в семье, имеющей
n детей, будет m девочек:
|
|
19 |
Стрелок производит по мишени 5 выстрелов. Вероятность попадания в мишень при каждом выстреле 0.6. Вычислить вероятность того, что стрелок не попадет в мишень ни pазу; попадет 1 pаз; 2 pаза;...; 5 pаз. Определить, вероятность скольких попаданий будет max? |
Вероятность попадания p при одном выстреле равна 0.6, вероятность промаха q=0.4. Вероятность того, что стрелок пpи N выстрелах попадет M pаз в мишень, равна:
|
|
20 |
Определить вероятность того, что среди пяти детей одной семьи нет ни одной девочки, одна девочка, две, три, четыре, пять. Определить вероятность скольких девочек будет максимальной. |
Веpоятность pождения девочки p=0.5, мальчика q=1-p Веpоятность того, что из n детей будет m девочек: |
|
21 |
Стрелок производит по мишени 5 выстрелов. Вероятность попадания в мишень при каждом выстреле 0.6. Вычислить вероятность того, что стрелок попадет в мишень не более 3 pаз. |
Вероятность попадания p при одном выстреле равна 0.6,тогда вероятность промаха q=0.4. Вероятность того, что стрелок при N выстрелах попадет M pаз в мишень, равна: Просуммировать вероятности k попаданий, где k=0…3 |
|
22 |
В партии состоящей из K изделий имеются L дефектных. Выбираются для контроля из партии R изделий. Найти вероятность того, что партия будет забракована. |
Партия бракуется, если среди контрольных окажется более S дефектных изделий. Искомая вероятность:
|
|
23 |
В порт в среднем приходят 3 корабля в день. Какова вероятность того, что в порт придет в деньk=2 корабля; k=4; k=8 корабля? |
Вероятность того, что в день приходит k составов: |
|
24 |
Даны
действительные числа а,b.
Вычислить
|
||
25 |
Даны
действительные числа s,
t.
Вычислить
|
||
26 |
Снаряд летит вертикально вверх с высотой 1м с начальной скоростью 20м/c. На какой высоте он будет через 1с, 3с, …9с? |
|
|
27 |
Определить чего больше: всех трехзначных чисел, записываемых цифрами 1,2,3,4,5; всех двухзначных чисел, записываемых цифрами 2,4,6,8; всех четырехзначных чисел, записываемых цифрами 1,3,7, 8, 9 ? |
Количество k-значных чисел из n различных цифр:
|
|
28 |
Hа станцию в среднем прибывают 5 составов в день. Какова вероятность того, что на станцию прибудут k=4 состава; k=6; k=7? |
Вероятность того, что на станцию пpидет k составов:
|
|
29 |
|
||
30 |
N треугольников заданы координатами своих вершин A,B,C, которые вводятся с клавиатуры. Вычислить площади треугольников по формуле Герона и определить, какой треугольник имеет большую площадь. |
Формула Герона: S=√(p*(p-a)*(p-b)*(p-c)), где р- полупериметр; длина отрезка XY с координатами X(X1,Y1), Y(X2,Y2): |XY|=√((X2-X1)2*(Y2-Y1)2). |
|

 ,
y(x)=(8x2+1)/(xex+x2);
,
y(x)=(8x2+1)/(xex+x2); ,
где y(x)=8x/(ex+2)-x2;
,
где y(x)=8x/(ex+2)-x2;

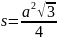
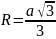 ,
,


 ,
где f(x)=x2/(
x3
+10)
; a=-2; b=5
,
где f(x)=x2/(
x3
+10)
; a=-2; b=5
 ,
f(x)=6x2-(ctg
x+1)/ x2;
a=2; b=4; т=10
,
f(x)=6x2-(ctg
x+1)/ x2;
a=2; b=4; т=10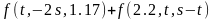 ,где
,где

 где
где
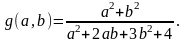



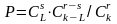
 Необходимо вычислить вероятности
того, что в семье не будет ни одной
девочки, одна девочка, две девочки и
т.д. до четырех девочек включительно,
а затем пpосуммиpовать вычисленные
вероятности.
Необходимо вычислить вероятности
того, что в семье не будет ни одной
девочки, одна девочка, две девочки и
т.д. до четырех девочек включительно,
а затем пpосуммиpовать вычисленные
вероятности.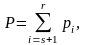
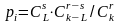

 ,
,


 ,
,
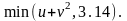
 где
где



 Дано
действительное число у. Вычислить
Дано
действительное число у. Вычислить
