§ 1. Анализ индивидуальных убытков
Модели страхования жизни делятся на две большие группы: краткосрочное страхование – сроком на один год и долгосрочное – более одного года.
Рассмотрим
простейший вид краткосрочного страхования
жизни. Человек платит страховой компании
рублей (страховая
премия), а
компания выплачивает наследникам
застрахованного
рублей в случае смерти человека в течение
года, и не платит ничего, если застрахованный
не умрет в течение года. Величину
называют страховой
выплатой. И
важнейшей задачей является определение
зависимостей между величинами
и
.
Застрахованный,
купив за
рублей страховой полис, избавил себя
от риска финансовых потерь, связанных
с неопределенностью момента смерти.
Этот риск приняла на себя страховая
компания, и риск заключается в случайности
убытка по рассматриваемому договору.
Этот индивидуальный
убыток
является элементарной составляющей
финансового риска компании и представляет
собой случайную величину
с законом распределения
-
0
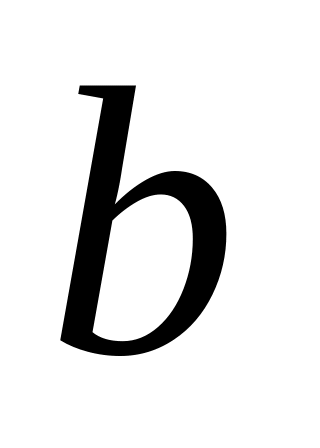
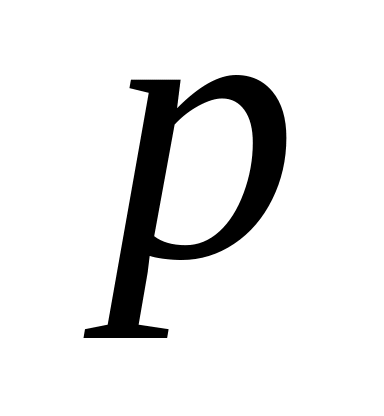
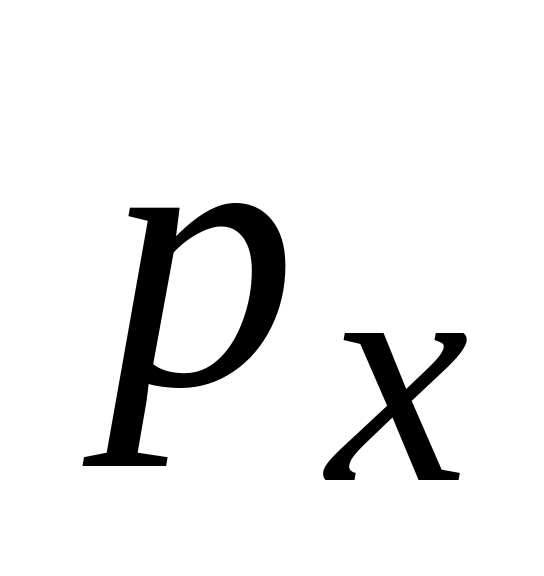
Здесь
- вероятность смерти в течение года
застрахованного в возрасте х
лет; а
.
Средняя величина убытка (математическое ожидание) равна
,
(1)
а дисперсия –
.
(2)
Наряду с величиной
рассмотрим и случайную величину
,
описывающую потери страховой компании
от заключенного договора страхования
Вычислим математическое ожидание потерь компании:
.
(3)
Так как средние
потери компании должны быть неположительными,
то есть
,
то
или
.
А минимально возможное значение
,
удовлетворяющее последнему неравенству,
равно
,
(4)
и называется нетто-премией.
Таким образом, нетто-премия соответствует средним нулевым потерям компании.
На самом деле
реальная плата
за страховку должна быть больше
,
так как, во-первых, компания должна
учитывать фактор случайности
,
во-вторых, в сумму
входят и различные организационные
затраты. Плата
должна при этом гарантировать малую
вероятность разорения компании. Разница
между премией
и нетто-премией
называется страховой надбавкой
(защитная надбавка, надбавка за
безопасность), а величина
(5)
называется относительной страховой надбавкой. Страховая надбавка необходима для защиты компании от разорения в виду случайности вариаций индивидуальных исков.
Таким образом, общая плата за страховку, без учета организационных затрат, имеет вид:
.
(6)