§ 2. Пропорциональное перестрахование

2.1. Чистое пропорциональное перестрахование

При этом виде перестрахования страховщик передает перестраховщику одинаковую долю от всех рисков страхового портфеля, которые он принимает в одной и той же отрасли. То есть перестраховщик покрывает одну и ту же часть исков во всех страховых случаях, оплаченных страховщиком.

Пусть портфель страховой компании состоит из договоров страхования с исками . Тогда, при наступлении страхового случая, сумму платит передающая компания, а сумму выплачивает перестраховочная компания.

Таким образом, суммарный иск к страховой компании

уменьшается и становится равным

.

Однако одновременно уменьшается и капитал передающей компании.

До заключения договора перестрахования капитал передающей компании был равен

, (1)

где - относительная страховая надбавка, обеспечивающая страхователю определенную вероятность неразорения . Заключение договора перестрахования приводит к выплате перестраховочной компании суммы

, (2)

где - относительная страховая надбавка, установленная перестрахователем. Поэтому капитал передающей компании станет равным:

. (3)

Следовательно, вероятность неразорения передающей компании становится равной

,

или

. (4)

При аппроксимации нормальным распределением, получаем:

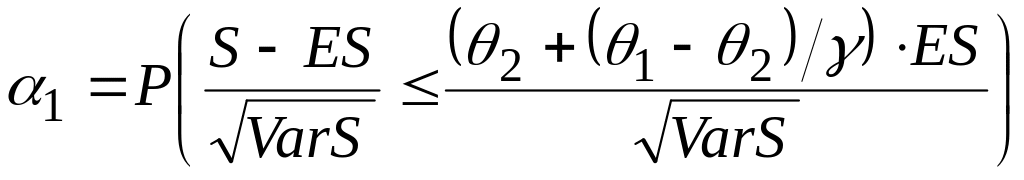, (4´)

где

-

квантиль нормального распределения.

Отсюда следует, что для максимизации вероятности неразорения необходимо выбрать параметр таким образом, чтобы максимизировать величину .

Видно, что:

а) Если , то есть , то максимум достигается при . Другими словами, если перестраховочная компания устанавливает меньшую страховую надбавку , то нужно перестраховать все иски. При этом вероятность разорения будет равна нулю. Однако этот случай практического интереса не имеет, так как реально справедливо равенство .

б) Если , то есть , то . Другими словами, если перестраховочная компания устанавливает большую страховую надбавку, то от перестрахования нужно вообще отказаться.

в) Если , то есть , то вероятность неразорения от не зависит. Другими словами, может принимать все значения в промежутке .

Следовательно, в рамках простейшей модели риска (без учета неоднородности договоров, резервов и различного рода издержек) чистое пропорциональное перестрахование не представляет никакого интереса с точки зрения математики.

2.2. Пропорциональное эксцедентное перестрахование

При этом виде перестрахования предел удержания может меняться по рискам в пределах , , где - количество различных договоров страхования. Тогда перестраховочной компании будет выплачена сумма:

.

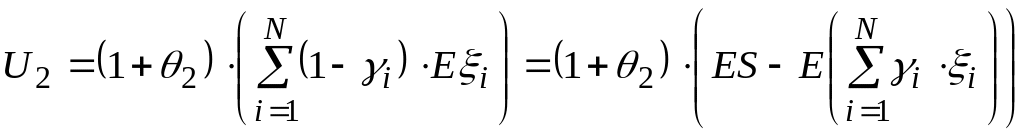Поэтому капитал передающей компании становится равным

, (5)

а вероятность неразорения можно вычислить как

. (6)

Рекомендуется устанавливать значения таким образом, чтобы оставалось постоянным. То есть по некоторым рискам удержание будет полным, а по остальным . Здесь - полная страховая премия по - ому договору. В соответствующих договорах оформляют таблицу уровней удержания, величина которых уменьшается с увеличением интенсивности рисков.