Нетто-премия будет вычисляться как:

. (15)

№ 8. Решите № 7 при условии заключения договора о трехлетнем чисто накопительном страховании.

Решение. Воспользуемся формулой:

.

Тогда, если продолжительность жизни описывается моделью де Муавра, получаем:

(55,94%).

Ответ: 55,94%.

Если же в № 8 воспользоваться упрощающими функциями, то:

(57,51%).

Видно, действительно, что аппроксимация законов продолжительности жизни моделью де Муавра несколько искажает результаты вычисления нетто-премий.

2.4. п-летнее временное страхование жизни

При этом виде страхования нетто-премия вычисляется по формуле

. (16)

№ 9. Решите № 7 при условии заключения договора трехлетнего временного страхования жизни.

Решение. Воспользуемся формулой:

.

Тогда:

(2,57%).

Ответ: 2,57%.

2.5. п-летнее смешанное страхование жизни

Нетто-премия вычисляется по формуле:

. (17)

№ 10. Решить № 7 при условии заключения договора трехлетнего смешанного страхования жизни.

Решение. Согласно формуле:

,

получаем:

(58,51 %).

Ответ: 58,51%

2.6. Полное страхование жизни, отсроченное на т лет

При этом виде страхования нетто-премия вычисляется по формуле:

. (18)

№ 11. Решить № 7 при условии заключения договора полного страхования жизни, отсроченного на три года.

Решение. Согласно формуле:

,

получаем:

(3,52%).

Ответ: 3,52%.

2.7. п-летнее временное страхование жизни, отсроченное на т лет

(19)

2.8. Полное страхование жизни с непрерывно возрастающим пособием

. (20)

№ 12. Решить № 7 при условии заключения договора полного страхования жизни с непрерывно увеличивающимся возмещением.

Решение. Согласно формуле

,

получаем:

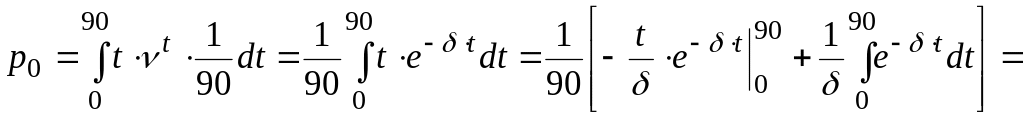
(33,43 %).

Ответ: 33,43 %.

§ 3. Расчет нетто-премий для основных дискретных видов страхования

Исходя из определения дискретных видов страхования, и понятия актуарной стоимости можно получить следующие формулы для вычисления нетто-премий:

1. Полное страхование жизни с выплатой страхового пособия в конце последнего года жизни.

Нетто-премия вычисляется как

. (21)

где

, (22)

является дискретным анализом непрерывной упрощающей функции .

2. п-летнее временное страхование жизни с выплатой пособия в конце года смерти

. (23)

3. п-летнее смешанное страхование жизни с выплатой пособия в конце года смерти

. (24)

где .

4. Полное страхование жизни с выплатой страхового пособия в конце последнего года жизни, отсроченное на т лет

. (25)

5. Полное страхование жизни с ежегодно возрастающем пособием и выплатой пособия в конце последнего года жизни

. (26)

Обозначив , можем записать в виде

.

Здесь - это дискретная упрощающая функция.

§ 4. Связь между непрерывными и дискретными видами страхования

В предыдущем параграфе мы рассмотрели дискретное страхование жизни, когда страховая сумма выплачивается в конце года смерти. Это предположение не отражает реальной практики страхования, но имеет то преимущество, что вычисления можно проводить непосредственно по таблицам продолжительности жизни.

Кроме того, вычислив нетто-премии при дискретном страховании жизни, можно вычислить и нетто-премии при соответствующих видах непрерывного страхования. Для того чтобы связать между собой непрерывные и дискретные виды страхования необходимо сделать определенные предположения о законе распределения времени жизни для дробных возрастов.

Обычно предполагают, что этот закон – равномерный. Известно, что в этом случае случайные величины и независимы, и имеет равномерное распределение на . Тогда можем получить следующие формулы, связывающие нетто-премии для соответствующих непрерывных и дискретных видов страхования:

. (27)

, (28)

, (29)

, (30)

. (31)

Таким образом, приведенные выше формулы позволяют вычислять разовые нетто-премии по непрерывным видам страхования через характеристики , , , которые достаточно просто вычисляются по данным, приводимым в общих таблицах продолжительности жизни.

Во всех иллюстративных примерах, которые мы будем приводить в дальнейшем, предполагаем, при необходимости, что распределение смертей внутри года носит равномерный характер.