18.1. Напряжения и деформации железобетона при сжатии

Железобетонные элементы, подвергаемые осевому сжатию (рис. 18.1), армируют в основном продольными и поперечными стержнями (хомутами). Поперечная арматура необходима для:

- препятствия выпучиванию продольной арматуры при сжатии;

- обеспечения соединения отдельных продольных стержней в плоские и простран­ственные каркасы.

При осевом сжатии железобетонных элементов деформации в арматуре и прилегающем слое бетона равны и выражаются по формуле.

, (18.1)

где - напряжения в арматуре и бетоне;

- модуль упругости арматуры и бетона;

-

Уравнение (18.1) представляет собой условие совместности деформаций арматуры и бетона.

С другой стороны, из условия равновесия элемента можно соста­вить уравнение, выражающее равенство между внешним усилием N и внутренними усилиями, действующими в бетоне и продольной арматуре:

N= (18.2)

где F_а - площадь продольной арматуры;F_а - площадь сечения бе­тона. Из (18.1) получим напряжение в арматуре

(18.3)

где п=Е_а/Е_б - коэффициент приведения.

Подставляя формулу (18.3) в (18.2), получим:

(18.4)

где - коэффициент армирования.

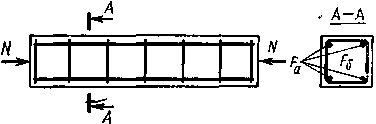
Рис. 18.1. Осевое сжатие железобетонного элемента

Напряжения в бетоне и арматуре зависят от коэффициента упру­гости , который связан с напряжением нелинейной зависимостью. Кроме того, коэффициент при длительном выдерживании элемен­та под нагрузкой вследствие развития деформаций ползучести уменьшается, что приводит к снижению напряжений в бетоне. При этом напряжения в арматуре, как следует из условия (18.2), долж­ны возрастать. Таким образом, с течением времени происходит пе­рераспределение внутренних усилий между бетоном и арматурой.

При увеличении внешней нагрузки напряжения в бетоне дости­гают предела прочности при сжатии Rnp, а в арматуре, согласно формуле (18.3),-величины так как при разру­шении ≈0,25. Из выражения (18.3) следует, что предельные на­пряжения в арматуре перед разрушением железобетонных элемен­тов, подвергаемых сжатию, зависят не только от механических свойств стали, но и от упругопластических свойств бетона, что учи­тывается при установлении расчетного сопротивления арматуры сжатию.

18.2. Напряжения и деформации железобетона при растяжении

При осевом растяжении железобетонного элемента различают три характерные стадии напряженно-деформированного состояния.

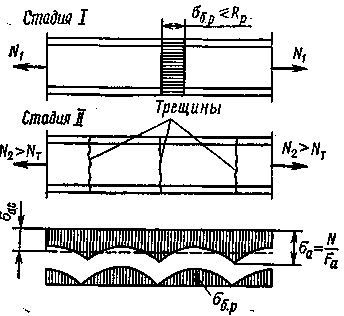
Рис. 18.2. Напряженное состояние при осевом растяжении

В стадии I напряженно-деформированного состояния в элемен­те нет трещин, напряжения в бетоне и одинаковы во всех сечениях (рис. 18.2). Деформации бетона и арматуры равны по всей длине элемента, так как сцепление между ними не нарушено:

(18.5)

Напряжение в арматуре

(18.6)

По мере увеличения на­грузки наступает конечный этап стадии I, предшествующий образованию трещин в бетоне. Напряжения в бетоне достига­ют предела прочности на растя­жение, а деформации, согласно формуле (18.5),-величины

На основании опытов можно принять 0,5; тогда

(18.7)

Усилие, вызывающее появление трещин, будет равно сумме уси­лий в бетоне и арматуре:

N_т =R_p F+2nR_p F_a =R_p (F+2nF_a). (18.8)

При дальнейшем увеличении нагрузки в бетоне появляются тре­щины, наступает стадия // напряженно-деформированного состоя­ния, при которой в сечениях, проходящих через трещины, сопротив­ление растяжению оказывает только арматура, а в сечениях между трещинами - арматура и бетон. По мере удаления от трещин на­пряжения в арматуре убывают, а в бетоне возрастают, так как в работу включается бетон, расположенный на участке между трещи­нами, в пределах которого сцепление с арматурой остается ненару­шенным.

В стадии /// напряжения в арматуре достигают временного соп­ротивления R_a и железобетонный элемент разрушается при усилии N=F_a.R_a