20.2. Расчет прочности по нормальным сечениям

Предельное состояние балки по несущей способности характеризуется разрушением либо в нормальном к оси элемента сечении 7, либо в наклонном 2 (рис. '20.6). Разрушение по нормальному сечению вызывается действием изгибающего момента, а по наклонному - действием поперечных сил и реже моментов.

В железобетонных нормально армированных изгибаемых элементах разрушение начинается с растянутой арматуры. По достижении в ней предела текучести резко уменьшается высота сжатой зоны бетона, что вызывает ее разрушение.

В соответствии с описанным характером разрушения железобетонных балок по нормальным сечениям существует два случая расчета:

а) первый случай, когда расчет ведется в предположении, что первопричиной разрушения элемента будет достижение в растянутой арматуре расчетных сопротивлений;

б) второй случай, когда расчет ведется в предположении, что прочность элемента исчерпывается вследствие разрушения сжатой зоны бетона раньше, чем напряжения в растянутой арматуре достигают расчетного сопротивления.

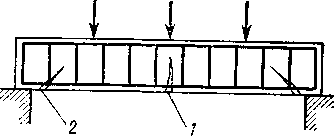
Рис. 20.6. Разрушение балки:

1 — по нормальному сечению; 2 — по наклонному

Элементы с одиночной арматурой. При первом случае расчета предельное состояние элементов с одиночной арматурой, т. е. с рабочей арматурой, расположенной только в растянутой зоне, если площадь арматуры не превышает некоторого предела, характеризуется достижением арматурой расчетного сопротивления R_а, а затем или одновременно (но не ранее) -достижением бетоном расчетного сопротивления сжатию. В предельном состоянии внутренние усилия будут равны: в растянутой арматуре-R_а.F_а, в сжатом бетоне при прямоугольной эпюре напряжения - R_прF_б (рис. 20.7, а).

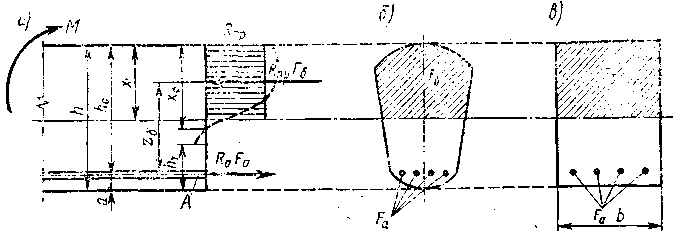
Рис. 20.7. К расчету элемента с одиночной арматурой

Выведем расчетные формулы для элементов с сечением любой формы, симметричной относительно вертикальной оси (рис. 20.7, б), исходя из двух условий равновесия в предельном состоянии.

Уравнение моментов относительно оси, проходящей через точку приложения равнодействующей усилий в растянутой арматуре А:

или

Очевидно, несущая способность элемента будет обеспечена, если внешний момент не превысит величину предельного момента внутренних сил; поэтому можно записать

(20.1)

(20.2)

где S_б - статический момент площади сжатой зоны бетона относительно оси, нормальной к плоскости действия изгибающего момента и проходящей через точку приложения равнодействующей усилия в арматуре А.

Положение нейтральной оси, а следовательно, и площадь сжатой зоны бетона определяют из уравнения проекций на ось элемента:

или . (20.3)

В расчет изгибаемых элементов вводится не полная высота сечения h, а рабочая - полезная h₀=h-а, где а - расстояние от равнодействующей усилий в арматуре Л до растянутой грани балки (рис. 20.7, в). Отношение высоты сжатой зоны сечения к рабочей высоте называют относительной высотой сжатой зоны сечения ξ=x/h₀. Величины х и h₀ измеряют в направлении, перпендикулярном к прямой, ограничивающей сжатую зону.

С увеличением количества растянутой арматуры, как видно из уравнения (20.3), увеличивается площадь сжатой зоны бетона F_б, а следовательно, х и ξ. Очевидно, что существует граничное значение ξ_R и соответствующее предельное армирование, при превышении которого разрушение элемента будет начинаться уж не с растянутой арматуры, а со сжатой грани бетона. Это и будет границей между первым и вторым случаями расчета элемента.

Таким образом, расчет элементов по первому случаю, по формулам (20.1) и (20.3), производится, если ξ=x/h₀≤ξ_R. При ξ>ξ_R расчет ведется по второму случаю. Опыты показали, что величина ^д зависит от свойств бетона и арматуры. С увеличением прочности бетона ввиду его меньшей пластичности наблюдается более раннее хрупкое разрушение сжатой зоны бетона, что ведет к уменьшению значений ξ_R. При увеличении же прочностных свойств арматуры ξ_R уменьшается.

На основании опытных данных получена следующая эмпирическая формула для определения граничного значения относительно высоты сжатой зоны:

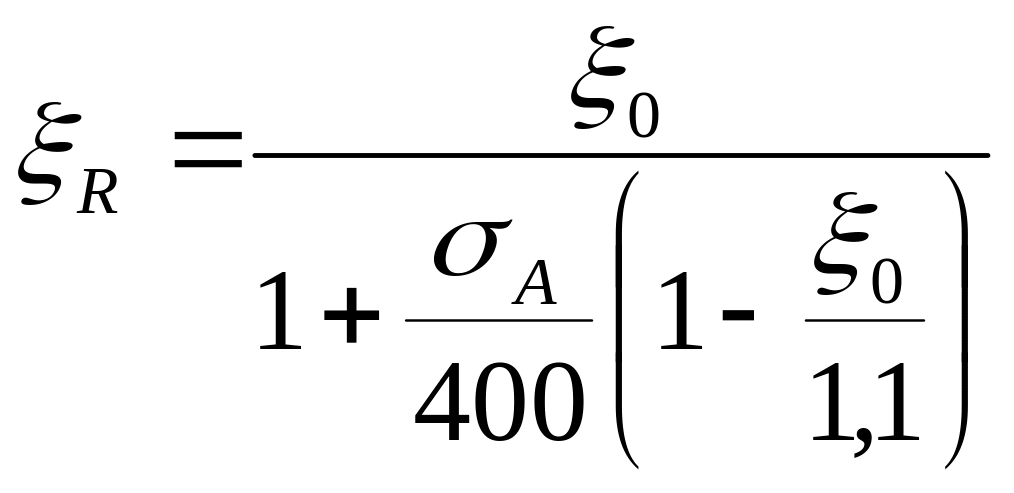, (20.4)

где ξ₀ - относительная высота условной сжатой зоны, соответствующая нулевым напряжением в арматуре, которая для элементов из обычного тяжелого бетона определяется по формуле

. (20.5)

В формулах (20.4) и (20.5) σ_A и R_пр в МПа.

Для элементов с арматурой классов A-I, A-II, A-III, B-I и Вр-1 в формулу (20.4) подставляют σ_A=R_а, для других видов арматуры, применяемой в предварительно напряженных конструкциях, значения σ_а принимают в соответствии с указаниями, приведенными в гл.23.

При использовании в расчете коэффициента условия работы бетона wci^O.SS в формуле (20.4) вместо 400 МПа подставляют 500 МПа.

Для элементов прямоугольного сечения (рис. 20.7, в) формулы (20.1) и (20.3) после подстановки в них F_б=bх и S_б=bх(h₀-х/2) примут вид

; (20.6)

. (20.7)

Из формулы (20.7) находят величину х,, определяющую положение нейтральной оси и площадь сжатой зоны бетона:

или

, (20.8)

где μ=F_а/bh₀ - коэффициент армирования (отношение сечения растянутой арматуры к рабочей площади сечения bh₀).

Относительное содержание арматуры в сечении можно выразить также через процент армирования: μ=F_а/bh₀ 100 %.

Из формулы (20.8) видно, что с увеличением μ увеличивается относительная высота сжатой зоны бетона ξ. Подставляя предельное значение относительной высоты сжатой зоны бетона в формулу (20.8), получим значение наибольшего коэффициента армирования

. (20.9)

Как видно из формулы (20.9), максимальный процент армирования μ_макс зависит от расчетных сопротивлений бетона и арматуры.

Например, для бетона М300 (R_np=13,5 МПа), армированного сталью класса A-III (R_а=340МПа); тогда μ_макс=0,58 (13,5/340) 100% =2,3%.

Вместе с тем нормы ограничивают и минимальные проценты армирования, установленные из условия равнопрочности армированного сечения с неармированным. Для изгибаемых элементов минимальное сечение рабочей растянутой арматуры Fa=0,0005 bh₀ (b - ширина прямоугольного сечения или ребра таврового сечения). Если процент армирования элемента ниже указанного минимума, его следует рассчитывать без учета арматуры, т. е. как неармированного бетонного элемента.

Чтобы упростить практические расчеты прямоугольных сечений, расчетные формулы преобразуют, выделяя в них параметры, для которых можно составить таблицу.

Формулу (20.6) можно представить так:

, (20.10)

где

, (20.11)

Уравнение моментов относительно центра тяжести сжатой зоны бетона.

, (20.12)

где

, (20.13)

Для прямоугольного сечения

. (20.14)

Таблица 20.1

Значения параметров для расчета изгибаемых элементов с одиночной арматурой

Ј	V	ао	Ј	V	ао	Ј	V	Ac
0,01	0.995	0,01	0,24	0,88	0,211	0,48	0,76	0,365
0,03	0,985	0,09	0,26	0,87	0,226	0,5	0.75	0,375
0,05	0,975	0,049	0,28	0,86	0,241	0,52	0,74	0,385
0,07	0,965	0,068	0,3	0,85	0.255	0,55	0,725	0,399
0.09	0,955	0,086	0,32	0,84	0,269	0,57	0,715	0,408
0,1	0.95	0,095	0,34	0,83	0,282	0.59	0,705	0,416
0,12	0,94	0,113	0,36	0,82	0,295	0,6	0,7	0,42
0,14	0,93	0,13	0,38	0,81	0,308	0,65	0,674	0,439
0,16	0,92	0,147	0,4	0,8	0,32	0,7	0,65	0,455
0,18	0.91	0,164	0,42	0,79	0,332	0,8	0,6	0,48
0,2	0,9	0,18	0,44	0,78	0,343	0,9	0,55	0.495
0,22	0,89	0,196	0,46	0,77	0,354	1	0,5	0,5

Из формулы (20.12) площадь сечения растянутой арматуры

. (20.15)

В табл. 20.1 даны численные значения А₀ и υ в зависимости от значений ξ.

При подборе сечений железобетонных элементов в практических расчетах следует иметь в виду, что одинаковая несущая способность может быть обеспечена при разных размерах сечения и соответственно процентах армирования. Из формулы (20.15), например, видно, что с увеличением высоты сечения элемента площадь сечения арматуры уменьшается. При проектировании конструкций необходимо стремиться к наиболее экономичному решению, при котором стоимость конструкции будет наименьшей.

Исследования показывают, что это требование соблюдается при ξ=0,2-0,3 для балок и ξ=0,1- 0,25- для плит.

Предельный момент, воспринимаемый элементом с одиночной арматурой, при котором бетон сжатой зоны не разрушается преждевременно, выражают формулой

, (20.16)

где

. (20.17)

Порядок расчета изгибаемых элементов с одиночной арматурой показан на численных примерах.