
- •5. Сетевые модели представления знаний. Семантические сети. Вычислительные сети.
- •Формализация
- •2. Языки инженерии знаний.
- •3 Средства автоматизации разработки экспертных систем.
- •20.Классификация систем распознавания образов.
- •Случай 3.
- •2.4.Нелинейные дискриминантные функции
- •2.4. Ф-машины
- •Потенциальные функции как дф
- •1)Постановка задачи
- •Отрицательный знак перед rk(X) выбирается так чтобы dk(X) представляла наиболее правдоподобный класс . То-есть чемь меньше rk(X) тем более правдоподобно , что Xk . (далее менее важное до п.2)
- •3) Принятие решения по максимуму правдоподобия
- •4) Ошибки классификации
- •1) Проблема выбора информативных признаков
Случай 3.
Каждый класс отделяется попарно от других классов, но отсутствуют области неопределенности В этом случае имеется М решающих функций.
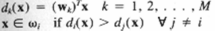
Многослойные машины
Двухслойная машина хорошо известна как коммитет, называется так потому, что в ней есть возможность голосования для каждой ЛДФ, определяющей свою классификацию
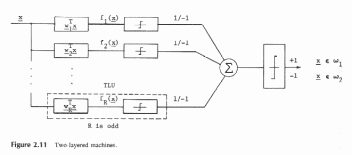
Первый слой_это часть до Σ и справа от него второй слой.
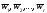 определяютr-различных ДФ, представляют
собойn-мерные вектора.
определяютr-различных ДФ, представляют
собойn-мерные вектора.
Первый слой состоит из нечеткого числа ДФ, чьи выходы клишируются пороговым логическим элементом как +1 или-1, в зависимости от значения f(x). Второй слой — это одна линейная поверхность с единичным весовым вектором, используемым для решения к какому классу окончательно относится вектор
2.4.Нелинейные дискриминантные функции
ЛДФ — это простейшие ДФ, но часто приходится использовать нелинейные ДФ (НЛДФ). Квадратическая функция имеет следующий вид:
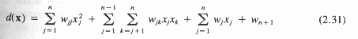
Полное число весов d(x) равно (n+1)(n+2)/2.
Отметим, что
если все собственные числа λ матрицы А
положительны, то квадратичная форма
xTAxникогда не будет отрицательной иxTAx=0,
если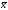 =
0. Это значит, что матрица А — положительно
определенная и квадратичная форма тоже
положительно определенная. Однако, если
один или более λ равно 0, в то время как
другие положительны, матрица А будет
положительно полуопределенной.
=
0. Это значит, что матрица А — положительно
определенная и квадратичная форма тоже
положительно определенная. Однако, если
один или более λ равно 0, в то время как
другие положительны, матрица А будет
положительно полуопределенной.
Вспомним, что решающая поверхность определяется как
dj(x) =di(x) илиdj(x) -di(x) = 0
Для квадратического случая квадратическая разделяющая поверхность определяется уравнением
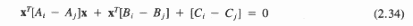
Варианты квадратической поверхности будут определяться матрицей А=(Ai-Aj). Если А положительно определена, то решающая поверхность будет гиперэллипсоидом с осями в направлении собственных чисел. Если А=aI- единичная матрица, то реш. поверхность будет гиперсферой. ЕслиA– положительно полуопределена решающая поверхность есть гиперэллипсоидальный цилиндр , состоящий из пересекающихся областей в виде гиперэллипсоидов меньшей чемnразмерности с осями в направлении ненулевых собственных векторов. В другом случае (когда А отрицательно определена) – решающая поверхность – гиперболоид.
2.4. Ф-машины
Ф-машины (φ) вид классификаторов, в которых для классификации используются φ функции. φ функция (обобщенная дискриминантная функция записывается в виде:
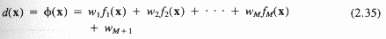
где fi(x);i=1,…,M- линейно независимо вещественные, однозначно определенные функции, независимые отWi.
Отметим, что φ(х) – линейно относительно Wi, однако,fi(x)- необязательно предполагается линейным.
Потенциальные функции как дф
Потенциальная
функция ψ(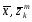 )
известна как ядро в оценке плотности
вероятности, или есть функция Х иZkm, определенная в пространстве образов,
гдеZkm
–m-ый прототип,
определяющий классwk.
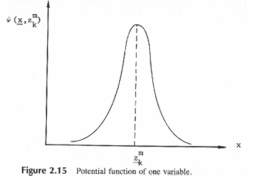
Потенциальная функция хорошо иллюстрируется
на рис. 2.15 для одномерного пространства
образов. Этот потенциал определяет
уменьшающееся соотношение между точкойZkm
и точкой х по мере того, как расстояниеd(x,Zkm)
между двумя точками увеличивается.
)
известна как ядро в оценке плотности
вероятности, или есть функция Х иZkm, определенная в пространстве образов,
гдеZkm
–m-ый прототип,
определяющий классwk.
Потенциальная функция хорошо иллюстрируется
на рис. 2.15 для одномерного пространства
образов. Этот потенциал определяет
уменьшающееся соотношение между точкойZkm
и точкой х по мере того, как расстояниеd(x,Zkm)
между двумя точками увеличивается.
Суперпозиция индивидуальных ядер потенциальных функций будет использоваться как ДФ
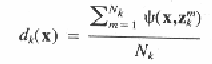
которая определена для класса К, где Nk– число прототипов в классе К. Функции ψ могут различать классы или даже прототипы между внутри класса. Для ψ желательны следующие характеристики:
ψ(x,z) должна быть максимальна приx=z.
ψ(x,z) должна быть приближенно равна 0 дляxотличающегося отzв заданной области.
ψ(x,z) должна быть гладкой (непрерывной) функцией и стремиться к монотонному уменьшению с увеличением дистанцииd(x,z)
Если ψ(x1,z) = ψ(x2,z), образыx1иx2должны иметь приблизительно одинаковую степень подобия сz.
Непараметрические методы обучение дискриминантных функций. Процедуры обучения с коррекцией ошибок.
Дискриминантная
функция — функция d(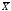 ),
которая определяет решающую поверхность.
),
которая определяет решающую поверхность.
Решающая поверхность, может быть формально определена как поверхность вn-мерном пространстве, разделяет известные образы на их соответствующие категории и используется для классификации неизвестных образов. Такие поверхности можно определить как гиперплоскости, имеющие размерностьn-1.
Вообще коррекция W (обучение) может быть сформулирована следующим образом:
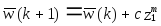 ,
если
,
если
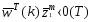
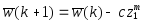 ,
если
,
если
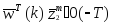
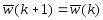 ,
если классифицировано правильно,
,
если классифицировано правильно,
где
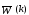 и
и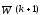 - весовые вектора наk-ом
и (k+1)-ом
шагу коррекции, соответственно. Добавление
корректирующего члена
- весовые вектора наk-ом
и (k+1)-ом
шагу коррекции, соответственно. Добавление
корректирующего члена
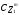 заставляет вектор
заставляет вектор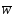 двигаться
в направлении
двигаться
в направлении .
.
Существует несколько правил выбора величины С (корректирующего члена):
1) Правило с фиксированной коррекцией
В этом алгоритме С - выбирается как фиксированная положительная константа. В целом процесс настройки весов будет закончен за конечное число шагов. Выбор С для этого процесса не очень важен. Если теорема сходимости справедлива для С=1, то она будет справедлива для любого С 1, так как изменение С фактически масштабирует все образы без изменения их разделимости.
2) Правило абсолютной коррекции
В
этом алгоритме С
выбирается
как наименьшее целое число, которое
передвигает
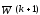 (вектор весов) поперек гиперплоскости
образа в область решенияw
каждый раз как классификатор делает
ошибку. Правило абсолютной коррекции
также дает решающий весовой вектор за
конечное число шагов.
(вектор весов) поперек гиперплоскости
образа в область решенияw
каждый раз как классификатор делает
ошибку. Правило абсолютной коррекции
также дает решающий весовой вектор за
конечное число шагов.
3) Правило с частичной коррекцией
В
алгоритме с частичной коррекцией С -
выбрано так, что
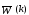
 двигается
на часть расстояния в направлении
нормали к желаемой гиперплоскости.
двигается
на часть расстояния в направлении
нормали к желаемой гиперплоскости.
Процедура обучения для всех перечисленных 3-х алгоритмов выглядит следующим образом:
1)
Взять любой
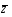 из обучающей последовательности и
проверитьd(z),
для определения класса (предполагается
М=2).
из обучающей последовательности и
проверитьd(z),
для определения класса (предполагается
М=2).
2)
Если получен правильный ответ, переходим
к следующему
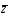
3) Если имеет место ошибочная классификация, изменяем w(k) на w(k+1).
4)
После того, как будут проверены все
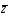 из обучающей
последовательности, повторяем все
процедуры заново в том же порядке. Если
из обучающей
последовательности, повторяем все
процедуры заново в том же порядке. Если
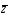 линейно
разделимы , все три алгоритма будут
сходиться к правильному
линейно
разделимы , все три алгоритма будут
сходиться к правильному
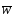 .
.
Градиентные методы
Общий метод градиентного спуска
Метод градиентного спуска является другим приближением к обучающим системам. Градиентный вектор обладает важным свойством указывающий максимальную скорость увеличения функции по мере увеличения аргумента. Процедура настройки весов может быть сформулирована как:
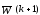 =
=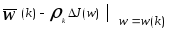 ,
,
где
J(w)
- критерий качества, который минимизируется
настройкой
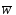 .
МинимумJ(w)
может быть достигнут передвижением
.
МинимумJ(w)
может быть достигнут передвижением
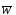 в
направлении отрицательного градиента.
Процедура может быть описана следующим
образом:
в
направлении отрицательного градиента.
Процедура может быть описана следующим
образом:
1.
Начать с некоторого произвольно
выбранного вектора w(1)
и вычислить градиентный вектор
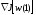
2. Получаем следующую величину w(2) передвигаясь на некоторое расстояние от w(1) в направлении наиболее крутого спуска.
kв уравнении - положительный скалярный множитель, который устанавливает размер шага.
Персептронная функция критерия
Пусть функция критерия будет:
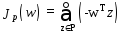
где суммирование осуществляется по неправильно классифицированным векторам образов. Геометрически Jp(w) пропорционально сумме расстояний неправильно классифицированных образов от гиперплоскости.
Возьмем производную от Jp(w) по w(k) :
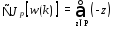 (3.32)
(3.32)
где w(k) означает величину w на k-ой итерации. Персептронный обучающий алгоритм может быть сформулирован как
w(k+1)
= w(k)
-
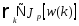 (3.33)
(3.33)
w(k+1)
= w(k)
+
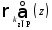 (3.34)
(3.34)
где Р - последовательность неправильно классифицированных образов при данном w(k).
Алгоритм обучения будет иметь вид
w(k+1) = w(k) +kz (3.37)
Байесовская дискриминантная функция. Принятие решение по максимуму правдоподобия. Ошибки классификации.
