Лабораторная работа № 5 Измерение удельной теплоемкости и удельной теплоты плавления парафина.

Цель работы

Исследовать зависимость температуры расплавленного парафина от времени в условиях постоянной теплоотдачи и опреде­ление удельной теплоемкости жидкого парафина и удельной теплоты плавления парафина.

Общие положения

При передаче твердому телу некоторого количества теплоты происходит увеличение амплитуда колебаний атомов или молекул в узлах кристаллической решетка, температура кристалла повышается достижении температуры плавления передача телу теплоты не сопровождается повышением температура до тех. пор, пока все те­ло не расплавится. В процессе плавлении твердого тела кинетическая энергия хаотического теплового движения атомов или молекул не меняется. Количество теплоты, получаемое твердым телом при плавлении, расходуется на увеличение потенциальной энергии частиц. После расплавления всего кристалла происходит дальнейшее повышение температуры.

При охлаждении расплава до температуры кристаллизации за счет уменьшения потенциальной энергии взаимодействия частиц внешней среде отдается такое количество тепла, какое было noлучено в процессе плавления. При этом кинетическая энергия атомов или молекул не изменяется, температура твердого тела остаётся постоянной до завершения кристаллизации всего расплава.

При постоянной мощности теплопередачи кривая зависимости температуры от времени нагревания кристалла или от времени охлаждения расплава должна иметь вид ломаной с горизонтальным участком в области температуры плавления или температуры кристаллизации. Располагая такой кривой, можно определить удельную теплоемкость и удельную теплоту плавления вещества.

Если известна мощность Р теплопередачи, то удельная теплоемкость С вещества связана с изменением Т, его температура за время t₁ выражением

Q₁ = pt₁ = m₁c₁T . Из уравнения следует .

Удельную теплоту плавления  можно найти по известной мощ­ности р теплопередачи и времени плавления льда, в течение кото­рого температура вещества остается неизменной.

Q₂ = pt₂ = m_1. Из уравнения следует

Осуществить теплопередачу от нагревателя к последующему ве­ществу с постоянной и достаточно точно известной мощностью до­вольно трудно. Значительно проще обеспечить процесс теплопереда­чи с постоянной мощностью р от нагретого исследуемого вещества в окружающее пространство. Для этого достаточно расплавить ис­следуемое вещество и предоставить ему возможность остывать при неизменных внешних условиях. Теплопередача нагретого вещества окружающим телам зависит в первую очередь от разности темпера­тур. При небольших изменениях разности температур мощность теплопередачи от нагретого тела окружающим телам можно считать постоянной.

Упрощенный вид кривой зависимости температуры вещества от времени при охлаждении расплавленного кристаллического тела представлен на рисунке. По такой кривой можно определить значе­ния изменения температуры Т, и времени t₁ для нахождения удельной теплоемкости вещества в жидком состоянии и времени t₂ кристаллизации для вычисления удельной теплоты кристалли­зации вещества, равной удельной теплоте плавления.

Мощность теплопередачи от нагретого тела с неизвестными тепловыми параметрами можно узнать, исследовав зависимость температуры от времени для тела массой m₂ такой же формы и размеров в тех же условиях из вещества с известной удельной теплоем­костью с₂.

Проведение эксперимента и обработка результатов

I. Взвесьте пластмассовый сосуд, налейте в него воду, нагретую до 60°С. Укрепите в штативе термометр таким образом, чтобы его конец находился на половине глубины жидкости в сосуде.

2. Запустите секундомер и снимите показание термометра. Да­лее записывайте показания термометра через одну минуту до тех пор, пока температура вода не снизится до 45°С.

3. Взвесьте сосуд с водой, найдите массу m₂ воды.

4. Вылейте воду из сосуда и налейте в него расплавленный парафин при температуре 60°С до того же уровня, до какого бы­ла налита вода. Укрепите термометр в штативе таким образом, что­бы его конец находился на половине глубины жидкого парафина в сосуде.

5. Запустите секундомер и снимите показания термометра. Далее записывайте показания термометра через одну минуту до тех пор, пока температура парафина не снизится до 45°С.

6. Взвесьте сосуд с парафином и найдите массу m₁ парафина.

7.Постройте график зависимости температуры от времени для воды.

По графику зависимости температуры воды от времени найди­те длительность интервала времени t₃ при изменении температу­ры воды T₂ = 10°С от 55°С до 45°С. По найденным значениям T₂, t₃, m₂ и известной удельной теплоемкости с₂ воды вычислите мощность Р теплопередачи при остывании.

8. Постройте график зависимости температуры от времени для парафина. Определите по графику значения времени t₁ остыва­ния жидкого парафина, изменения температуры Т₁ до затвердева­ния парафина. По найденным значениям t₁, T₁ и известным значениям m₁ и Р вычислите удельную теплоемкость жидкого пара­фина С₁.

9. Определите по графику зависимости температуры парафина от времени продолжительность времени t₂ его затвердевания. По найденному значению времени t₂. и известным значениям m₁, и Р вычислите удельную теплоту  кристаллизации (плавления) парафина.

Результаты измерений и вычислений занесите в отчетную таблицу.

Контрольные вопросы

1. Почему в опыте по определению удельной теплоты плавления парафина целесообразнее осуществить процесс кристаллизации, а не плавления?

2. Какими соображениями можно руководствоваться при выборе размеров сосуда для проведения опыта?

3. Докажите, что предположение о постоянной мощности теп­лопередачи в данном эксперименте близко к истине.

Лабораторная работа №6

Определение измерения энтропии

Цель работы

Опытным путем установить зависимость изменения энтропии от теплоемкости тел при выравнивании температур тел в изолированной адиабатической термодинамической системе.

Общие положения

Так же как и внутренняя энергия, энтропия является функцией состояния термодинамической системы. Если термодинамическая систе­ма получает в обратимом процессе количество теплоты δQ при тем­пературе Т, то отношение δQ /T определяет изменение энтропии dS системы, т.е. и для обратимого процесса является полным дифференциалом. На прак­тике обычно интересуются только изменением энтропии, а не ее абсо­лютным значением.

Изменение энтропии системы можно найти, используя второе на­чало термодинамики

где интеграл берется по пути термодинамического процесса между состояниями 1 и 2, где S₁ и S₂ - значения энтропии в этих состояниях. Знак равенства соответствует обратимому процессу, а знак неравенства - необратимому.

Второе начало термодинамики утверждает, что при обрати­мом процессе изменение энтропии системы равно интегралу от между состояниями 1 и 2 по обратимому пути и больше этого интегра­ла по пути необратимому, т.е. в этом случае интеграл от не выражает изменение энтропии, а меньше его.

Представляет интерес изучение изменения энтропии в изолиро­ванной адиабатической системе.

Изменение энтропии в изолированной адиабатической системе при квазистатическом (обратимом) процессе равно нулю, так как , т.е.

В случае необратимых процессов в изолированной адиабатической системе также равно нулю, но изменение энтропии в та­кой системе уже нулю не равно и по формуле для обратимых про­цессов не может быть вычислено. Это вычисление можно сделать, если учесть, что энтропия есть функция состояния системы и ее применение не зависит от характера пути процесса в системе, т.е. обратимого или необратимого. В этом случае для вычисления изменения энтропии можно воспользоваться любым квазистатическим (обратимым) процессом, переводящим систему из состояния 1 в 2, т.е.

В случае выравнивания температуры от T₁ до Т₂ твердых и жидких тел в изолированной адиабатической системе этот реальный процесс можно заменить изобарическим квазистатическим (обратимым) переходом теплоты между телами. При изобарическом процессе

где m - масса тела, с_Р – удельная теплоемкости тела при постоянном давлении. Для характеристики теплоемкости тел исполь­зуется также и удельная теплоемкость при постоянном объеме – c_V. У жидких и твердых тел разница между c_р и c_V сравнительно мала, так что можно положить c_p ≈ c_V и говорить просто об удель­ной теплоемкости жидких и твердых тел c. Нужно помнить, что удельная теплоемкость вещества c зависит от температуры, т.е. c = c(Т). Тогда изменение энтропии в этом процессе можно опре­делить

В нашем случае вместо c(Т) будем использовать среднее значе­ние удельной теплоемкости c в интервале температур от T₁ до Т₂ и считать для этого температурного интервала среднее зна­чение удельной теплоемкости c величиной постоянной, тогда изменение энтропии будем вычислять по формуле

В силу того, что энтропия аддитивна, полное изменение энтропии термодинамической системы можно найти, если просуммировать изме­нения энтропии всех отдельных тел, входящих в состав этой системы, т.е.

где ∆S - изменение энтропии всей системы; n - число тел системы; ∆S_i - изменение энтропии одного из тел термодинамиче­ской системы.

Согласно первому началу термодинамики, , сообщаемое термодинамической системе тепло идет на измене­ние внутренней энергии системы dU и совершение системой работы над внешними телами. В случае твердого и жидкого тел все сообщаемое тепло идет на изменение внутренней энергии, а так как объемы этих тел при нагревании почти не изменяются, то работой расширения можно пренебречь, т.е., чем больше измене­ние энтропии в адиабатно-изолированной системе, тем большее коли­чество тепла необратимо переходит во внутреннюю энергию системы. Поэтому необратимые потери тепла, связанные с реальными необратимы­ми термодинамическими процессами в адиабатно-изолированных систе­мах, принято оценивать по изменению энтропии.

Если в калориметр, содержащий определенное количество воды при заданной температуре, опустить нагретое тело, то произойдет теплообмен и установится общая температура. Сам калориметр поме­щен во внешний стакан, в результате чего система становится почти адиабатно-изолированной.

Термодинамическому равновесию адиабатической системы соответ­ствует состояние с максимумом энтропии, при этом температура вест частей системы в состоянии равновесия одинакова.

Изменение энтропии такой системы при выравнивании температу­ры погруженного тела и воды можно рассчитать по формулам 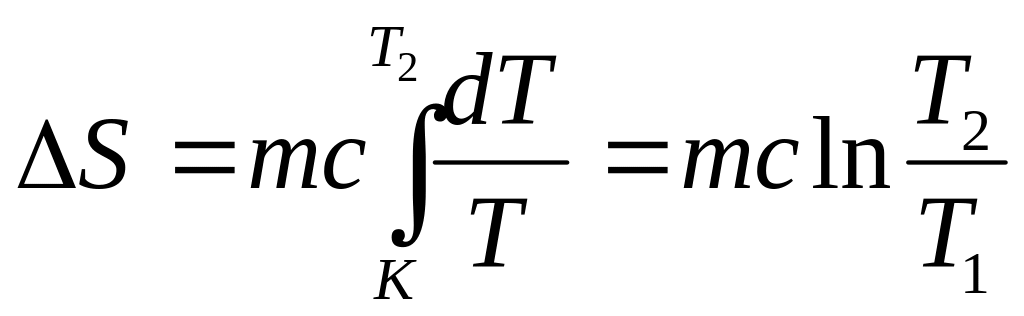и . В состав исследуемой системы входят: испытуемое тело массой m_T с удельной теплоемкостью с_T и начальной температурой Т₀, вода калориметра массой m_В с удельной теплоемкостью с_В и начальной температурой Т₀ . После окончания процесса теплообмена установится температура Т.

При выравнивании температуры энтропия каждого из тел изменя­ется:

Учитывая аддитивность энтропии, можно записать ∆S = ∆S₁ + ∆S₂ + ∆S₃.

Подставляя значения ∆S₁, ∆S₂, ∆S₃, получим расчетную формулу изменения энтропии всей системы

В данной работе

m_B = 0,2 кг; С_В = 4,1810³ Дж/кгК (при t=20ºC);

с_T (железо)= 440,5 Дж/кгК;

с_T (латунь)= 384,7 Дж/кгК;

с_T (алюминий)= 896,1 Дж/кгК.

В работе предлагается рассчитать изменение энтропии шести нагретых тел при опускании в калориметр с водой, температура и масса которой одинаковы в каждом эксперименте.