§ 6. Изменение уровня жидкостей в капиллярах.
В результате смачивания водой стеклянной капиллярной трубки образуется искривленная поверхность – мениск. Давление под этой поверхностью р понижено по сравнению с давлением р0 у плоской поверхности. В результате возникает выталкивающая сила, поднимающая жидкость в капилляре до тех пор, пока вес столба не уравновесит действующую силу. Поскольку объем жидкости обусловлен кривизной, можно предположить, что высота подъема тем больше, чем больше кривизна мениска, возрастающая по мере утончения просвета трубки.
Рассмотрим состояние равновесия двух объемных фаз α (газ) и β (жидкость), разделяемых искривленной поверхностью в форме сферического сегмента.
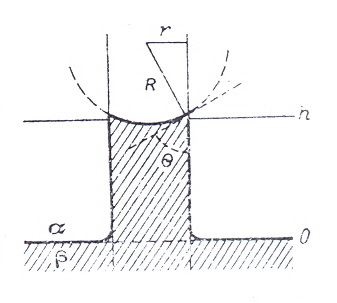
Равновесное состояние капиллярного поднятия жидкости: h – высота поднятия жидкости, 0 – нулевой уровень, R – радиус кривизны мениска, r – радиус трубки, Θ – краевой угол.
На нулевом уровне, отвечающем плоской поверхности, давление в обеих фазах в состоянии равновесия одинаково и равно р0 как внутри, так и снаружи трубки. На уровне h мениска давление pβ в фазе β меньше, чем на нулевом уровне в той же фазе, на величину гидростатического давления столба жидкости высотой h.
Это давление равно:
.
Поэтому
4.3.1
Аналогично
4.3.2
Тогда для
получим:
.
4.3.3
В соответствии с
геометрическим построением данного
рисунка можем показать, что
.
4.3.4
На основе уравнений 4.2.6, 4.3.3 и 4.3.4 получим уравнение Жюрена:
,
,
.
4.3.5
Если α – пар или воздух, то ρβ » ρα, и величиной ρα можно пренебречь:
4.3.6
В случае несмачивания cosΘ < 0 и в соответствии с уравнением 4.3.5 h < 0, т.е. уровень жидкость должен опускаться (например, ртуть в стеклянном капилляре).
В случае полного смачивания (cosΘ = 1) получается упрощенное выражение, часто используемое на практике при небольших краевых углах:
.
4.3.7
Из уравнений 4.3.5 – 4.3.7 видно, что чем меньше r, тем больше высота поднятия.
Для воды:
r = 1 мм, h = 1,5 см;
r = 1 мкм, h = 15 м;
r = 0,1 мкм, h = 150 м;
r = 1 нм, h = 15 км.
Капиллярное поднятие глубинных вод в грунтах и почвах обеспечивает существование растительного покрова Земли. Для предотвращения высыхания почвы применяются агротехнические мероприятия (например, боронование) с целью разрушения капиллярных каналов поверхностного слоя почвы.
§ 7. Химический потенциал и давление пара у искривленных поверхностей.
Рассмотрим малую сферическую каплю жидкой фазы α в фазе пара β. Используя уравнение для потенциала Гиббса для объемной фазы α при постоянных p и T, запишем:
.
4.4.1
,
;
,
.
Отсюда находим интересующую нас производную
,
4.4.2
где
– парциальный мольный объем i-го
компонента.
В процессе образования кривизны в однокомпонентной (i=1) двухфазной (α, β) системе при T, s и ni = const получим:
4.4.3
4.4.4
(см.§3)
Подставляя 4.4.4 в 4.4.3, получим:
,
4.4.5
в первом приближении можно считать постоянной.
Так как для воды при r = 10–7 м и σ = 73∙10–3 Н/м можно найти p = 1,5 МПа (15 атм). Эта величина мала по сравнению с внутренним давлением воды (≈103 МПа), и поэтому справедливо допущение, что в процессе искривления поверхности дополнительного сжатия жидкости не происходит.
Проинтегрируем
выражение 4.4.5 в пределах от плоской
поверхности (радиус r=
)
до искривленной поверхности (радиус
r).
вынесем за знак интегрирования, т.к.
считаем ее постоянной.
,
4.4.6
где
–
значение
вещества у плоской поверхности.
Из уравнения 4.4.6
следует, что
в капле выше, чем у плоской поверхности.
Но в состоянии равновесия
,
тогда, относя в уравнении 4.4.6 левую часть
к пару, а правую – к жидкости, можно
записать для идеальной системы
.
4.4.7
Над плоской поверхностью
.
4.4.8
Подставим 4.4.7 и 4.4.8 в выражение 4.4.6:
,
4.4.9
4.4.10
Уравнение 4.4.10 называется уравнением Томсона (лорда Кельвина). Оно показывает, что давление насыщенного пара над каплей будет тем больше, чем больше σ и меньше радиус капли r.
Например, для воды при изменении радиуса от 10–5 см до 10–6 см давление увеличивается на 1 %. Это следствие уравнения Томсона (Кельвина) позволяет предсказать наблюдаемое явление изотермической перегонки, заключающееся в испарении малых капель и конденсации пара на более крупных каплях, а также на плоской поверхности.
Над вогнутым
мениском жидкости
В этом случае радиус кривизны меняет
знак, и для сферического мениска
получается аналогичное уравнение
.
4.4.11