По Чебышеву
Сформируем коэффициент отражения ρ(p):
Воспользуемся рекккуретной формулой ( n3):
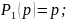
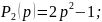
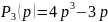– полином Чебышева
третьего порядка при n3;
Составим , выбирая знак “-” функции ρ(p):
;
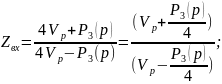
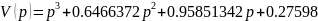Выберем верхние знаки:
Разложим функцию в цепную дробь (по Кауэру):
2p3 + 0,6466372p2 + 1,70851342p + 0,27598 2p3 + 0,6466372p2 + 0,85379p |
0,6466372p2 + 0,20851342p + 0,27598
|
3,094p → l1 |
|
0,855101p+ 0,27598 |
|
0,6466372p2 + 0,20851342p + 0,27598 0,6466372p2 + 0,20851342p
|
0,855101p+ 0,27598 |
0,756p→ c2 |
|
0,27598 |
|
0,855101p+ 0,27598 0,855101p |
0,27598 |
3,094p → l3 |
|
0,27598 |
|
0,27598 0,27598 |
0,27598 |
1 → r2 |
|
0 |
Цепная дробь будет иметь вид:
Полученной функции соответствует нормированная схема (Рисунок 3):
Рисунок 3 - Нормированная схема по Чебышеву
Если выбрать противоположные знаки «+» и « - » у функции , то получим дуальную нормированную схему фильтра, которой соответствует схема ФНЧ-прототипа (Рисунок 4):
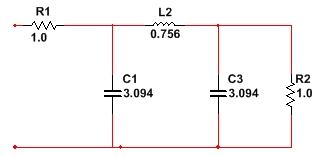
Рисунок 4 - Нормированная дуальная схема по Чебышеву
Переход от фнч-прототипа к фвч. Денормирование и расчет элементов схемы заданного фильтра
Обычно из двух дуальных схем ФНЧ-прототипа выбирают схему с большим числом индуктивностей, которые в результате перехода к схеме ФНЧ, преобразуются в емкость.
При переходе от ФНЧ-прототипа к ФВЧ, нормированные элементы схемы ФНЧ-прототипа заменяются на нормированные элементы схемы ФВЧ, индуктивность заменяется на ёмкость, а ёмкость – на индуктивность.
Осуществим
переход от нормированной схемы
ФНЧ-прототипа к схеме ФВЧ, учитывая то,
что каждая индуктивность Lк
переходит в емкость
,
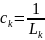а
каждая емкость
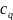
Для
преобразования передаточной функции
ФНЧ-прототипа в передаточную функцию
ФВЧ используется
.
По Баттерворту
А) Денормирование схемы:
Найдем преобразующие множители:
– преобразующий
множитель частоты;
– преобразующий
множитель по сопротивлению.
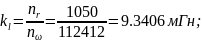
l1 = 0.747;
c2 =1.802;
l3 = 1.802;
c4 = 0.747;
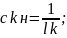
c1н= 1.3338688;
l2н= 0.554939;
c3н= 0.554939;
l4н= 1.3338688;
Расчеты:
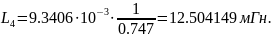
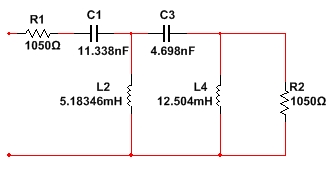
Рисунок 5 - Денормированная схема по Баттерворту
Б) Денормирование для второй дуальной схемы:
Найдем преобразующие множители:
– преобразующий множитель частоты;
– преобразующий множитель по сопротивлению.
l’2 = 1.802;
c’1 =0.747;
l’4 = 0.747;
c’3 = 1.802;
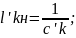
c’2н= 0.554939;
l’1н= 1.3338688;
c’4н= 1.3338688;
l’3н= 0.554939;
Расчеты:
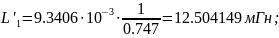
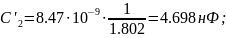
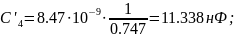
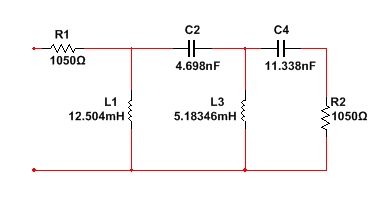
Рисунок 6 - Денормированная дуальная схема по Баттерворту