Нормирование фнч прототипа для фвч

;

;

;

Аппроксимация частотной характеристики рабочего ослабления фильтра Аппроксимация по Баттерворту

Аппроксимация по Баттерворту получила название монотонной, или максимально гладкой.

;

- коэффициент неравномерности рабочего ослабления в полосе пропускания.

Найдем порядок полинома Баттерворта:

Определим корни полинома Гурвица:

Определим передаточную функцию T(p):

Пользуясь формулой сокращенного умножения (a+b)(a-b)=(a² – b²) и помня, что j*j = -1, получаем:

Так как p=j, то:

Функция рабочего ослабления фильтра имеет вид:

Выполним проверку, подставив аппроксимированной функции А() на частотах 0; 1 в полосе пропускания и на частоте в полосе непропускания:

dA=2.6 дБ;

.

А_мин<A(3.5098).

Полученные значения удовлетворяют рабочим параметрам.

Аппроксимация по Чебышеву

Аппроксимация по Чебышеву получила название равноволновой. Число экстремумов в полосе пропускания, включая граничные частоты, зависит от технических требований к фильтру и равно (n+1).

;

Найдем порядок полинома Чебышева:

;

Найдем корни полинома Гурвица:

P₁= =

= -0.162 + j0.910;

P₂= =

= -0.323 + j0;

P₃= =

= -0.162 - j0.910;

Определим передаточную функцию T(p):

Подставив p=j, получаем:

;

Выполним проверку, подставив аппроксимированной функции А() на частотах 0; 1 в полосе пропускания и непропускания:

; dA=2.6 дБ;

А_мин<A( ).

Полученные результаты удовлетворяют рабочим параметрам.

Реализация схемы фнч-прототипа методом Дарлингтона

Способ реализации электрических фильтров по Дарлингтону основан на формировании функции z_вх(p) по передаточной функции T(p). Тогда получение схемы нагруженного фильтра можно свести к реализации двухполюсника путем разложения функции z_вх(p) в цепную дробь по Кауэру.

Примем во внимание, что при реализации по Дарлингтону в нормированных схемах r₁=1.

По Баттерворту

Используем полученную на этапе аппроксимации функцию T(p):

Сформируем коэффициент отражения ρ(p):

– полином Баттерворта четвертого порядка (n=4).

B_n ()=ⁿ,  ;

p=j ;

Составим , выбирая знак “-” функции ρ(p):

V(p)+B₄(p)= 2p⁴ + 2.678p³ + 3.585842p² + 2.81316669p + 1.1034935;

V(p)–B₄(p)= 2.678p³ + 3.585842p² + 2.81316669p + 1.1034935;

Разложим функцию в цепную дробь (по Кауэру):

2p4 + 2,678p3 + 3,585842p2 + 2,81316669p + 1,1034935 2p4 + 2,678p3 + 2,1008p2 + 0,824414p	2,678p3 + 3,585842p2 + 2,81316669p + 1,1034935
	0,747p → l1
1,486p2 + 1,98859p + 1,1034935
2,678p3 + 3,585842p2 + 2,81316669p + 1,1034935 2,678p3 + 3,585842p2 + 1,9884p	1,486p2 + 1,98859p + 1,1034935
	1,802p→ c2
0,8246p + 1,1034935
1,486p2 + 1,98859p + 1,1034935 1,486p2 + 1,98859p	0,8246p + 1,1034935
	1,802 p → l3
1,1034935
0,8246p + 1,1034935 0,8246p	1,1034935
	0,747p → c4
1,1034935
1,1034935 1,1034935	1,1034935
	1→ r2
0

Цепная дробь будет иметь вид:

Полученной функции соответствует нормированная схема (Рисунок 1):

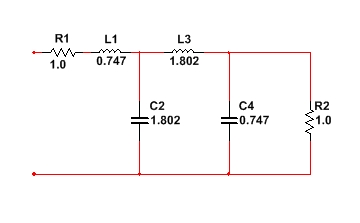
Рисунок 1 - Нормированная схема по Баттерворту

Если выбрать противоположные знаки “+” и “–” у функции , то получим дуальную нормированную схему фильтра, которой соответствует схема ФНЧ-прототипа (Рисунок 2):

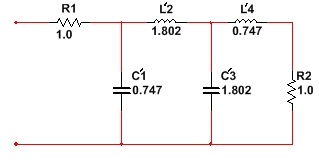
Рисунок 2 - Нормированная дуальная схема по Баттерворту