10.3. Уравнение парной регрессии

При статистическом изучении корреляционных зависимостей решаются две основные задачи:

1) нахождение формы связи между признаками и в виде математической формулы, выражающей эту зависимость;

2) измерение тесноты связи.

Эти задачи являются неразрывными и взаимно дополняющими друг друга задачами корреляционно-регрессионного анализа. Решение данных задач допускается в разной последовательности. В настоящем пособии сначала рассматривается нахождение уравнения регрессии, а затем – методы выявления и измерения тесноты связи.

Определение формы связи называется нахождением уравнения регрессии (уравнения связи).

Регрессия – это зависимость среднего значения случайной величины от одной или нескольких величин. Термин «регрессия» (от лат. regression – отступление, возврат к чему-либо) введен Ф. Гальтоном в 1886 г.

Парная регрессия позволяет получить аналитическое выражение связи между двумя признаками: факторным и результативным .

Найти уравнение регрессии – значит по фактическим (эмпирическим) данным математически описать изменения взаимно коррелируемых величин. Уравнение регрессии также называют теоретической линией регрессии – это линия, вокруг которой группируются точки корреляционного поля и которая указывает основное направление (основную тенденцию) связи. Теоретическая линия регрессии позволяет оценить среднее значение результативного признака при различных значениях факторного признака . При этом не должны учитываться все остальные факторы, влияющие на признак и не связанные с признаком .

Значения результативного признака, рассчитанные по уравнению регрессии, называются теоретическими . То есть, теоретические значения рассматриваются в виде функции, т.е. =

Аналитическая связь между признаками может описываться следующими уравнениями:

• прямая:

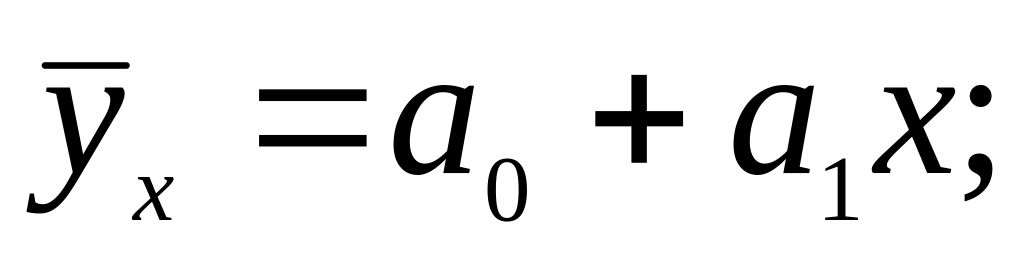
• парабола:

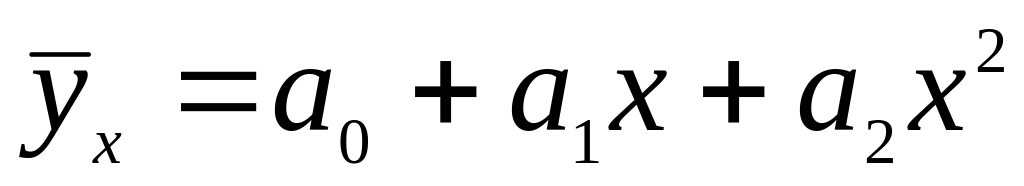
• гипербола: и др.

Считается, что если факторный и результативный признаки изменяются одинаково (примерно в арифметической прогрессии), то это свидетельствует о линейной связи между ними. Если признаки изменяются в разных направлениях, то связь является обратной. В этом случае применяется уравнение гиперболы. А если признаки изменяются в одном направлении, но с разной скоростью, то применяется параболическая или степенная функция.

После выбора типа функции определяют параметры уравнения регрессии. Параметры должны быть такими, чтобы рассчитанные с их помощью теоретические значения результативного признака , минимально бы отличались от фактических значений . То есть, теоретическая линия регрессии должна быть проведена так, чтобы сумма отклонений точек поля корреляции от соответствующих точек теоретической линии равнялась нулю ( ).

Уравнение парной линейной регрессии имеет вид:

,

где: - среднее значение результативного признака при определенном значении факторного признака; - свободный член уравнения (не имеет экономического смысла); - коэффициент регрессии, который показывает, на сколько единиц в среднем изменится результативный признак при изменении факторного признака на единицу его измерения. При такой интерпретации коэффициента регрессии предполагается, что сила воздействия признака на признак постоянна при любых значениях . С геометрической точки зрения коэффициент регрессии характеризует угол наклона лини регрессии к оси абсцисс.

Знак при коэффициенте регрессии показывает направление связи между признаками:

• при > 0 – связь прямая;

• при < 0 – связь обратная.

Параметры уравнения регрессии ( , ) определяются с помощью метода наименьших квадратов (МНК), согласно которому сумма квадратов отклонений теоретических значений результативного признака от фактических значений , была бы минимальной:

.

Рассмотрим парную линейную регрессию, так как линейная зависимость является наиболее используемой формой связи между двумя признаками.

Найдя частные производные указанной суммы по и , и, приравняв их нулю, получим систему нормальных уравнений при линейной парной регрессии:

где - объем исследуемой совокупности.

Решение этой системы дает параметры уравнения регрессии. Для нахождения параметров и при линейной зависимости могут использоваться готовые формулы:

;

Однако значения параметров и можно получить иначе. Если в системе нормальных уравнений каждое уравнение разделить на , то получим:

.

Теперь, зная значение , можно определить второй параметр уравнений регрессии:

Если связь выражена параболой, то для отыскания параметров уравнения , и применяется система нормальных уравнений вида:

Решив систему, получим уравнение регрессии вида:

.

Оценка обратной зависимости признаков и может быть осуществлена на основе уравнения гиперболы. Тогда для нахождения параметров уравнения гиперболы применяется система нормальных уравнений вида:

Также коэффициент регрессии можно рассчитать с помощью линейного коэффициент корреляции по формуле:

.

Коэффициент регрессии применяется для определения коэффициента эластичности , который показывает, на сколько процентов изменится в среднем величина результативного признака при изменении факторного признака на 1 %.

Коэффициент эластичности определяется по формуле:

Для большинства форм связи коэффициент эластичности является переменной величиной, т.е. изменяется в соответствии с изменением значений фактора .