7.3. Ошибки выборки

Выборочное наблюдение носит несплошной характер, поэтому оно сопровождается ошибками (погрешностями).

Ошибки выборочного наблюдения возникают в двух случаях: 1. при сборе данных (ошибки регистрации); 2. в результате неполного учета единиц генеральной совокупности (ошибки репрезентативности).

Таким образом, любому выборочному наблюдению свойственна ошибка репрезентативности - расхождение между характеристиками выборочной и генеральной совокупности (рис 7.1).

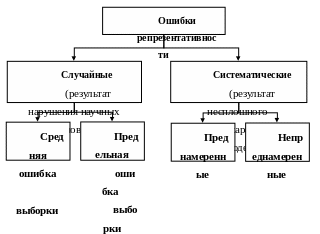
Рис 7.1. Виды ошибок репрезентативности

Ошибка репрезентативности возникает в результате того, что вы­борочная совокупность не полностью отражает закономерности, присущие генеральной совокупности. Величина случайной ошибки репрезентативности зависит:

1. от объема выборки;

2. от степени вариации признака в генеральной совокупности;

3. от метода отбора единиц и т.д.

По данным выборочной совокупности оценивают показатели (параметры) генеральной совокупности. Например, используют оценку 2-х параметров:

- генеральной средней величины изучаемого признака (для количественного признака);

- генеральной доли (для альтернативного признака).

Теоретическое обоснование появления случайных ошибок выборки объясняют предельные теоремы теории вероятностей. Так как случайная ошибка выборки возникает в результате случайных различий между границами выборочной и генераль­ной совокупностей, то при достаточно большом объеме выборки эта ошибка будет сколь угодно мала. Поэтому характеристики выборки могут достаточно хорошо представлять характеристики генеральной совокуп­ности. Случайные ошибки могут быть доведены до незначительных размеров, что позволит определить их размеры и пределы с достаточной степенью точности на основании закона больших чисел.

Выборочное распределение средней величины будет прибли­жаться к нормальному распределению по мере увеличения объема выборки , незави­симо от характера распределения генеральной совокупности. С увеличением численности выборки величина выборочной средней приближается к генеральной средней .

Одной из задач выборочного метода является определение ошибок выборки, т.е. возможных расхождений характеристик совокупностей:

1. между выборочной средней ( ) и генеральной средней ( );

2. между выборочной долей еди­ниц , обладающих изучаемым признаком, и генеральной до­лей (р).

Методы математиче­ской статистики позволяют измерить эти ошибки и указать границы их колеблемости. Величину ошибок можно оценить по формулам:

; .

В статистике различают три вида ошибок выборки:

- средняя ошибка ;

- предельная ошибка ;

- относительная ошибка .

Вид формулы средней ошибки выборки зависит от метода отбора. Рассмотрим порядок расчета ошибок выборки при собственно-случайном отборе.

Средняя ошибка выборки - характеризует среднюю величи­ну возможных расхождений выборочных (средняя , доля ) и генеральных характеристик (средняя , доля ) совокупности. Представляет собой среднее квадратическое отклонение возможных значений характеристик выборочной совокупности от характеристик генеральной совокупности.

Рассмотрим формулы средней ошибки выборки для средней и доли при повторном и бесповторном отборе: