9. Зразки розв’язання задач Задача 1.

Підприємство виробляє два види продукції. Для виготовлення першого виду продукції використовують два види ресурсів: сировина і електроенергія, витрати яких на одиницю продукції і місячні запаси наведено у таблиці.

Вихідний ресурс	Витрати вихідного ресурсу на одиницю продукції, грн.		Запаси, грн.
	І вид	ІІ вид
Сировина	0,8	0,5	400
Електроенергія	0,4	0,8	365

Вивчення ринку збуту показало, що місячний попит на І вид продукції перевищує попит на ІІ вид не більше ніж на 100 кг. Окрім того, встановлено, що попит на І вид продукції не перевищує 350 кг за місяць. Роздрібна ціна одиниці продукції І виду - 16 грн., а ІІ – 14 грн.

Яку кількість кожного виду продукції повинно щомісяця виробляти підприємство, щоб виручка від реалізації продукції була максимальною?

Розв’яжемо задачу за допомогою графічного методу

Позначимо: через - місячний обсяг випуску продукції І виду, кг; через - місячний обсяг випуску продукції ІІ виду, кг.

Складемо економіко-математичну модель задачі.

За критерій оцінки приймемо виручку від реалізації продукції (В), яка визначається за формулою

,

де - ціна одиниці і-го виду продукції, грн.; - обсяги виробленої продукції, кг.

Цільова функція буде мати вигляд

при обмеженнях

Знайдемо область припустимих розв’язків.

1. ,

2. ,

3. ,

4.

5. - І чверть.

Областю припустимих розв’язків є п’ятикутник .

Для знаходження екстремальних значень цільової функції при графічному розв’язку знайдемо вектор , який є градієнтом функції

.

Проводимо лінію рівня , яка є перпендикулярною до вектора . Оскільки цільова функція досліджується на максимум, то переміщується лінія рівня за напрямком вектора . Точкою виходу з області припустимих значень є точка , координати якої визначаються як перетин прямих та . Розв’язком системи є значення кг і кг.

Таким чином, найбільше значення функції або максимальна виручка від реалізації продукції складе

Задача №2

Підприємство виробляє три види продукції. Для виготовлення кожного виду продукції використовують два види ресурсів: сировина і електроенергія, витрати яких на одиницю продукції і місячні запаси наведено у таблиці.

Вихідний ресурс	Витрати вихідного ресурсу на одиницю продукції, тис. грн.			Запаси, тис. грн.
	І вид	ІІ вид	ІІІ вид
Сировина	2	1	3	200
Електроенергія	1	2	1	300

Роздрібна ціна одиниці продукції І виду - 3 тис. грн., ІІ виду – 4 тис. грн., ІІІ виду – 2 тис. грн.

Яку кількість кожного виду продукції повинно щомісяця виробляти підприємство, щоб виручка від реалізації продукції був максимальним?

Розв’яжемо задачу за допомогою симплексного методу

при обмеженнях

Переведемо економіко-математичну модель до канонічного вигляду

Складемо симплексну таблицю першого кроку

	БЗ	3	4	2	0	0
0		2	1	3	1	0	200
0		1	2	1	0	1	300
		-3	-4	-2	0	0	0

Заповнимо індексний рядок для змінних за формулами

і для вільного члена

.

Оскільки, маємо від’ємні оцінки при умові, що цільова функція , то знайдений розв’язок не є оптимальним. Складемо симплексну таблицю другого кроку.

За ключовий стовпець обираємо четвертий стовпець, який відповідає найменшому значенню індексної оцінки -4, а за індексний елемент 2, тому що найменше значення відношення вільного члена до відповідного елемента ключового стовпця .

	БЗ	3	4	2	0	0
0			0		1		50
4			1		0		150
		-1	0	0	0	2	600

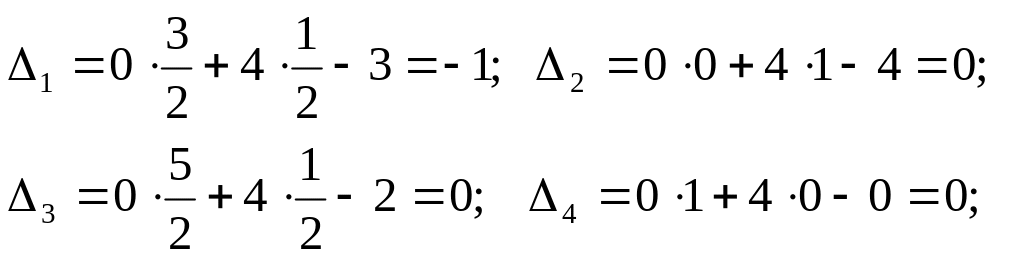
Оскільки, маємо від’ємну оцінку при умові, що цільова функція , то знайдений розв’язок не є оптимальним. Складемо симплексну таблицю третього кроку.

За ключовий стовпець обираємо третій стовпець, який відповідає від’ємному значенню індексної оцінки -1, а за індексний елемент , тому що найменше значення відношення вільного члена до відповідного елемента ключового стовпця .

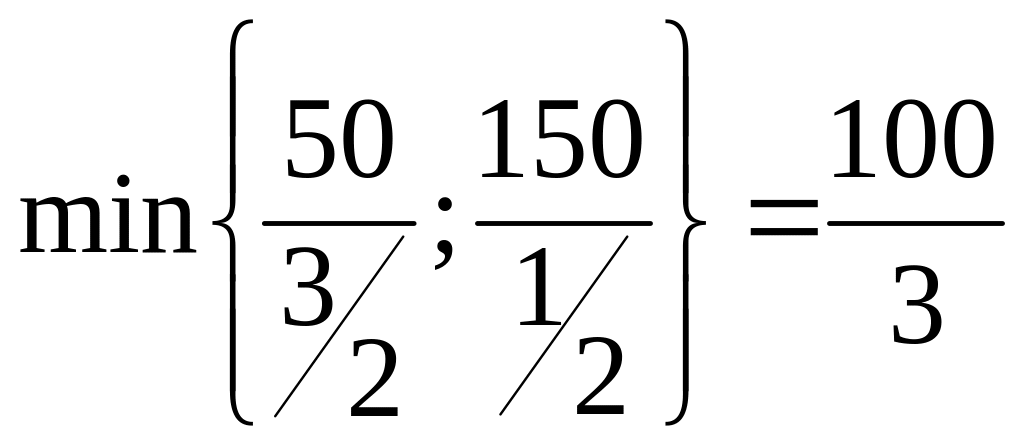	БЗ	3	4	2	0	0
3		1	0
4		0	1
		0	0

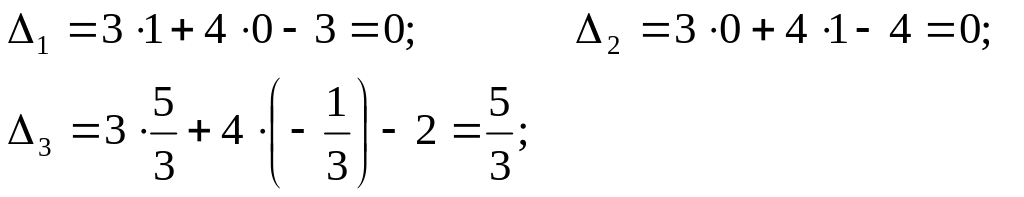
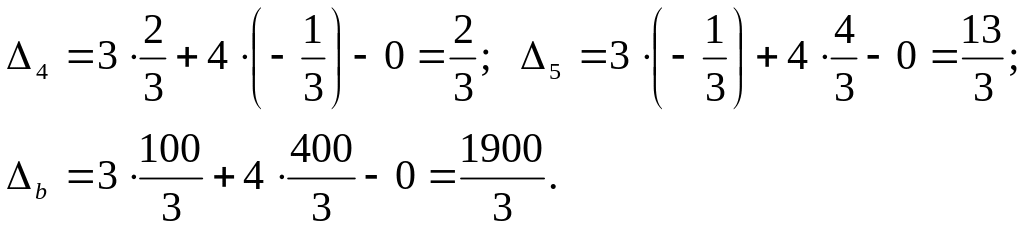
Оскільки, всі оцінки при умові, що цільова функція , то знайдений розв’язок є оптимальним.

Таким чином, підприємству необхідно виробляти продукцію І і ІІ виду, а випуск продукції ІІІ виду припинити.