Рішення|розв'язання|
Використовуватимемо рівняння Лагранжа у вигляді|виді|
.
(2.46)
Як узагальнена координата
приймаємо, як і раніше, переміщення тіла
1 з його початкового положення
.
Відповідний вираз для узагальненої
сили був отриманий вище (2.44), в якому
потрібно буде врахувати, що набули
значення гальмівного моменту MТ
= 58,9 Нм.
Складемо вираз|вираження| кінетичній енергії механічної системи. Нагадаємо, що кінетична енергія - це визначено позитивна величина, рівна сумі кінетичних енергій тіл, що входять в систему
,
(2.47)
для системи з одним ступенем свободи всі Тi мають бути виражені через інерційні параметри тіл і прийняту узагальнену швидкість.
Тіло 1 здійснює|скоює|
поступальний рух
з|із|
швидкістю
,
тому
.
Тіло 2 здійснює|скоює|
обертальний рух з|із|
кутовою швидкістю
,
.
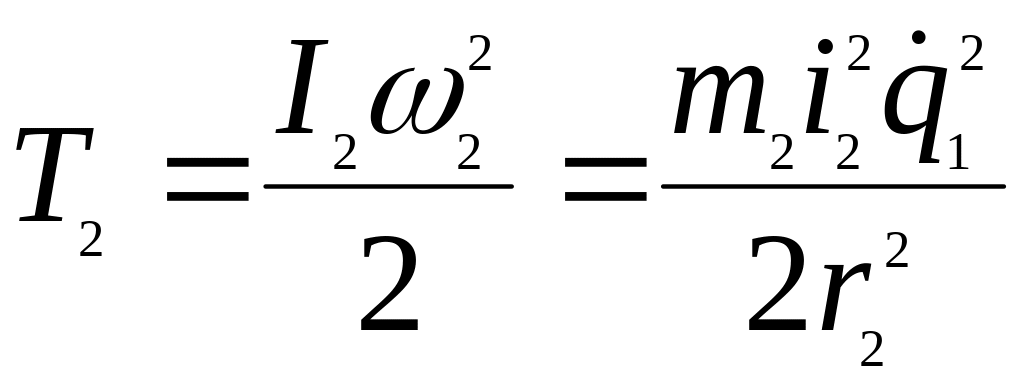У останній формулі враховано,
що момент інерції тіла складної форми
щодо|відносно|
осі обертання визначається як
добуток|добуток|
його маси на квадрат його радіусу інерції
.
Нагадаємо, що радіусом інерції тіла
щодо|відносно|
осі називається та відстань від осі, на
якій слід було б розташувати
точкову|крапкову|
масу, рівну масі тіла, щоб|аби|
момент інерції точкової|крапкової|
маси щодо|відносно|
осі дорівнював би моменту інерції тіла.
На цьому етапі рішення задачі
обчислимо|обчислятимемо|
значення моментів інерції тіл 2 і 3. Ці
тіла схожі, але|та|
не подібні, вони мають різні відношення
лінійних розмірів
.
кгм2,
кгм2.
Тільки подібні тіла мають однакові радіуси інерції i. Цю обставину використовують конструктори для полегшення розрахунків при обчисленні моментів інерції подібних тіл, прикладами яких можуть служити ротори электоических генераторів і двигунів різних потужностей, але подібні по конструкції, блоки зубчатих коліс в редукторах різних потужностей, підшипники однієї конструкції, але різних типоразмеров, ротори вентиляторів і тому подібне.
Тіло 3 здійснює плоско-паралельний рух, його рух можна розглядати як поступальне разом з центром мас і обертальне навколо центру мас або як обертальне в дану мить навколо миттєвої осі, що проходить через миттєвий центр швидкостей, позначений на рис 2.2 буквою Р- точка контакту колеса з нерухомою підставою. У першому варіанті можемо написати
,
де ω3 – угловая швидкість тіла 3
Vc3 – лінійна швидкість центру мас (центру тяжіння) колеса 3
Ic3 – момент інерції колеса 3 щодо осі, що проходить через його центр мас.
Вираз для
отримаємо, скориставшись виразом для
,
отриманим вище, враховуючи, що
співвідношення між можливими переміщеннями
і швидкостями відповідних точок механізму
однакові. У виразі
міняємо
на
і
на V1 =
.
Тепер
,
. Підставляємо отримані вирази в
загальну формулу для Т3.
.
Отримаємо тепер вираз для Т3, розглядаючи плоско-паралельний рух колеса 3 як обертання в дану мить часу з кутовою швидкістю навколо миттєвої осі, що проходить через міттєвий центр швидкостей Р (рис.2.2), тоді
,
де -
момент інерції колеса 3 щодо осі, що
проходить через міттєвий
центр швидкостей Р.
По теоремі Гюйгенса**
.
Отримуємо|одержуємо|
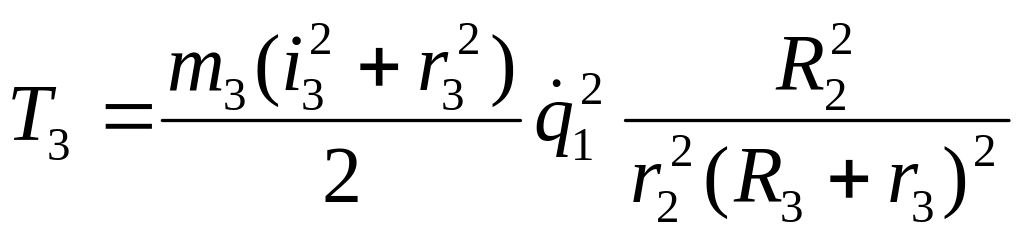, тобто, природно, тей ж саме вираз.
|вираження|
**Гюйгенс Християн (14.04.1629 – 8.07.1695) голландський фізик, механік, математик і астроном. Теорема, про яку йде мова|промова|, доведена Г. у зв'язку з винаходом і дослідженням сконструйованих їм першого маятникового годинника.
Підставляємо отримані|одержувати| вирази для Тi в (2.46)
,
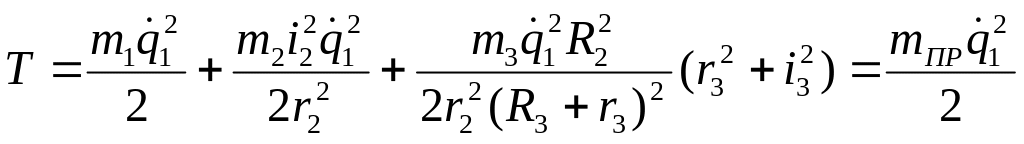(2.48)
де
називається приведеною масою механізму,
вона має розмірність [кг] в даному
прикладі при лінійній узагальненій
координаті
.
Якби|аби|
ми вибрали як узагальнену координату
кутове|
переміщення тіла 2,
то загальний|спільний|
для механізму вираз|вираження|
кінетичній енергії мав би вигляд|вид|
,
де
називається приведеним моментом інерції
механізму, він вимірюється в [кгм2]
(радимо цю формулу отримати самостійно,
склавши вираз кінетичній енергії
механізму, виразив лінійні і кутові
швидкості тіл через похідну від
узагальненої координати
).
Іноді для повнішої інформації про
прийняту узагальнену координату говорять
в першому варіанті: « Приведена до маси
m1
маса механізму» і в другому варіанті:
« Приведений до тіла 2 момент інерції
механізму».
Отримаємо|одержуватимемо| тепер диференціальне рівняння руху механізму за допомогою рівняння Лагранжа (2.46) для варіанту узагальненої координати .
Використовуємо вираз|вираження| кінетичній енергії механізму (2.48) і отримуємо|одержуємо| необхідні вирази похідних:
.
Підставляємо в рівняння Лагранжа (2.46) отримані|одержувати| вирази для похідних від кінетичної енергії і вираз|вираження| для узагальненої сили (2.44)
.
Приводимо|призводимо| рівняння до канонічного вигляду|виду| (коефіцієнт при вищій похідній повинен дорівнювати|рівнятися| 1)
.
(2.49)
Права частина|частка| отриманого|одержувати| диференціального| рівняння постійна, судячи по сенсу|змісту| другої похідної від лінійного переміщення тіла 1, це значення прискорення тіла 1, тому зручно ввести|запроваджувати| позначення
.
(2.50)
Тепер диференціальне рівняння руху механізму з|із| одним ступенем свободи (рис. 2.1) набуває|придбаває| найбільш простого вигляду|вид|, як рівняння руху матеріальної точки|точки|, при дії на неї постійних сил
.
(2.51)
Для диференціального рівняння другого порядку відповідно до вимог Коши*** необхідно сформулювати дві початкові умови. У даному завданні механізм починає рух із стану спокою і із положення, відповідного початку відліку прийнятої узагальненої координати, тобто при t=0
1)
2)
.
(2.52)
Интегруем (2.51)
,
,
где С1 и С2 –постійні інтегрування.
Використовуючи початкові
умови (2.52), отримуєм:
,
.
Виконуєм необхідні обчислення:
=
кг.
м/с2
З умови, що необхідно знайти
швідкість тіла 1 у той момонт часу, коли
його шлях S1=2
м, з рівняння руху
знаходим
=0,75
с, отже швидкість тіла 1 в цей момент
часу
м/с.
*** Огюстен Луї Коши (1789 - 1857) видатний|визначний| французький математик, написав понад 800 наукових робіт по різних розділах математики: геометрії, теорії чисел, математичному аналізу, математичній фізиці, алгебрі, дифереренціальному| і інтегральному численню|обчисленню|.
Ропай Валерій Андрійович
Науменко Олена Генадіївна
Киба В’ячеслав Якович
ЗАСТОСУВАННЯ|вживання| РІВНЯНЬ ЛАГРАНЖА II РОДА ДО РІШЕННЯ|розв'язання| ЗАДАЧ|задач| ДИНАМІКИ МЕХАНІЧНИХ СИСТЕМ.
Методичні рекомендації до розділу курсу теоретичної механіки
«Аналітична динаміка»
для студентів всіх форм навчання|вчення|
Редактор О.Н. Ільченко
Підписано до друку 20.04.2013. Формат 30х42/2
Папір офсет. Ризографія. Ум. друк. Арк. 2.9
Обл-вид арк. 2,5. Тираж 40 прим. Зам. №
Вищий навчальний заклад
«Національний гірничий університет»