Тема 5. Средние величины

1. Средние величины: сущность и значение.

2. Виды средних величин и условия их применения.

3. Математические свойства средней арифметической взвешенной и средней гармонической взвешенной величины.

4. Мода и медиана: понятие, область применения

Рекомендуемая литература по теме 5

1. Ниворожкина Л.И. Статистика: Учебник для бакалавров / Л.И. Ниворожкина [и др.]; под общ. ред. д.э.н, проф. Л.И. Ниворожкиной – М.: Издательско-торговая корпорация «Дашков и Ко», 2010. – 416 с.

2. Годин А. М. Статистика: учебник / А. М. Годин. – 2-е изд., перераб. – М.: Дашков и К, 2003. – с. 119 – 127.

3. Статистика: Учебник / Под ред. В.С. Мхитаряна. – М.: Экономисть, 2005. – с. 137 – 144.

4. Статистика: Учебник / И.И Елисеева, И.И. Егорова и др.; Под ред. проф. И.И. Елисеевой. – М.: ТК Велби, Изд-во Проспект. 2004. – с. 50 – 61.

5. Статистика: Учебник / под ред. И.И. Елисеевой. – М.: Высшее образование, 2009. – с.76 – 79.

6. Статистика: учебно-методическое пособие / М.Г. Назаров, В.С. Варагин, Т.Б. Великанова (и др.); под ред. д-ра экон. наук, проф., акад. Межд. акад. информ. и РАЕН М.Г. Назарова. – М.: КНОРУС, 2006. – с. 46 – 58.

Учебно-методические разработки кафедры

1. Наливкина Н.И., Иванова Е.М. Статистика: сборник задач к практическим занятиям / Н.И. Наливкина, Е.М. Иванова.; Краснояр. гос. торг.– экон. ин–т. – Красноярск, 2007, – 32 с.

2. Статистика : тесты для программированного контроля / Краснояр. гос. торг. – экон. ин-т ; сост. Е. В. Поклонова. – Красноярск: КГТЭИ, 2004. – 39с.

3. Наливкина, Н. И. Средние величины: текст лекции / Н. И. Наливкина; Краснояр. Гос. торг.-экон. ин-т. – Красноярск: КГТЭИ, 2008. – 36с.

4. Поклонова Е.В., Железко О.Е. СТАТИСТИКА: учебный словарь терминов для направления подготовки 080100.62 «ЭКОНОМИКА/ Е.В. Поклонова, О.Е. Железко; Краснояр. гос. торг.-экон. ин-т, Красноярск. – 2010.- 52 с.

Тесты для контроля усвоения материала по теме 5

1. Обобщающий показатель, в котором взаимно погашается влияние случайных факторов и выявляется типичная величина признака, называется … величиной.

2. Из нижеприведенных признаков выберете свойства средних величин:

1. есть индивидуальная характеристика;

2. есть обобщающая количественная характеристика совокупности

3. рассчитывается по атрибутивным показателям;

4. находится в виде суммирования;

5. метод познания от частного к общему;

6. применяется вместе с методом статистических группировок.

3. Выберете верные утверждения для средней величины:

1. для получения всесторонних знаний необходимо рассчитывать систему средних величин;

2. значение средней величины может быть выше максимального индивидуального значения;

3. значение средней не может быть меньше минимального индивидуального значения;

4. для расчета средний нужно понимать соотношение признаков в показателе;

5. осредняемый признак не должен быть количественным.

4. Имеются следующие виды средних величин:

a)

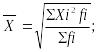
b)

c) .

Укажите: среднюю арифметическую взвешенную

среднюю квадратическую взвешенную

среднюю геометрическую простую

5. Имеются следующие виды средних величин:

a) ;

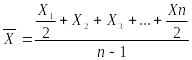b) ;

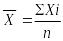c) ;

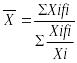6. Имеются следующие данные:

Цена за 1кг, руб.	50,00	30,00	25,00
Продано, кг	10	15	4

Рассчитайте среднюю цену за 1 кг. товара. Какая средняя была использована?

7. Определите среднесписочную численность за 1 квартал. Какую среднюю применяли?

на: 1.01 – 30чел.

1.02 – 28чел.

1.03 – 31чел.

1.04 – 34чел.

8. Средняя от постоянного значения признака равна:

1. нулю;

2. постоянному значению;

3. постоянному значению в квадрате.

9. Произведение средней на сумму весов (частот) равно:

1. нулю;

2. самой средней;

3. сумме произведения вариант на частоту.

10. «Весом» (частотой) в средней величине принимают:

1. индивидуальное значение признака;

2. частоту повторения одинаковых значений признака у единиц по объекту;

3. количество единиц объекта.

10. Средняя величина альтернативного признака равна:

1. доле единиц совокупности, обладающих альтернативным признаком;

2. доле единиц совокупности, не обладающих альтернативным признаком;

3. произведению долей единиц, обладающих и единиц, не обладающих альтернативным признаком.

7. Если увеличить каждую частоту в 5 раз и уменьшить каждое значение признака в 5 раз, то значение средней арифметической взвешенной:

1. не изменится;

2. увеличится в 5 раз;

3. уменьшится в 5 раз;

4. изменение нельзя предсказать.

7. Если каждое значение признака Х увеличить на 20 единиц, то значение средней арифметической взвешенной:

1. не изменится;

2. увеличится на 20 единиц;

3. увеличится в 20 раз;

4. изменение нельзя предсказать.

7. Если уменьшить каждое значение признака Х на 10 единиц, то значение средней арифметической взвешенной:

1. не изменится;

2. уменьшится на 10 единиц;

3. уменьшится в 10 раз;

4. изменение нельзя предсказать.

7. Если каждую частоту ( f) увеличить на 20 единиц, то значение средней арифметической взвешенной:

1. не изменится;

2. увеличится на 20 единиц;

3. увеличится в 20 раз;

4. изменение нельзя предсказать.

7. Если уменьшить каждое значение признака (Х) в 10 раз, то значение средней арифметической взвешенной:

1. не изменится;

2. уменьшится на 10 единиц;

3. уменьшится в 10 раз;

4. изменение нельзя предсказать.

7. Если уменьшить каждое значение признака (Х) в 10 раз и одновременно уменьшить каждую частоту (f) также в 10 раз, то значение средней арифметической взвешенной:

1. не изменится;

2. уменьшится в 100 раз;

3. уменьшится в 10 раз;

4. изменение нельзя предсказать.

7. Если уменьшить каждую частоту (f) в 10 раз, то значение средней арифметической взвешенной:

1. не изменится;

2. уменьшится на 10 единиц;

3. уменьшится в 10 раз;

4. изменение нельзя предсказать.

19. «Вариантом» в средней величине принимают:

1. количество единиц объекта;

2. частоту повторения одинаковых зна- чений признака у единиц объекта;

3. индивидуальное значение признака у единиц объекта.

20.Если вес (частота) в средней величине выражена абсолютной величиной, то сумма весов равна:

1. 100;

2. 0;

3. составу объекта по единицам (n).

21. Имеются следующие данные:

Размер заработной платы, тыс. руб.	3,5	4,0	5,5
Удельный вес работников, %	25,00	24,00	51,00

Рассчитайте среднюю заработную плату 1 работника. Какую среднюю будете применять?

22. Если вес (частота) в средней величине выражена в долях (в относительной форме), то сумма весов равна:

1. 0;

2. 100;

3. составу объекта по единицам.

23. Если при расчете средней все варианты изменять на одну и ту же величину, то средняя…:

1. не изменится;

2. изменится на ту же величину;

3. будет равняться нулю;

4. изменится в такое же количество раз.

24. Если при расчете средней все варианты изменять в одно и тоже число раз, то средняя…:

1. будет равняться нулю;

2. не изменится;

3. изменится на ту же величину;

4. изменится в такое же количество раз.

25. Если по каждой единице совокупности известен размер признака, выраженный абсолютной величиной, то расчет средней величины признака производится по формуле:

1. арифметическая простой;

2. арифметической взвешенной;

3. гармонической взвешенной;

4. квадратической взвешенной;

5. геометрической.

25. Если в каждой группе совокупности известны величина признака и количество единиц (частота), то для расчета средней величины применяется средняя:

1. арифметическая простая;

2. арифметическая взвешенная;

3. гармоническая простая;

4. гармоническая взвешенная.

25. Если в средней арифметической взвешенной каждое значение признака Х увеличить на одну и туже величину, то средняя:

1. не изменится;

2. увеличится на туже величину;

3. увеличится во столько же раз.

25. Если в средней арифметической взвешенной каждую частоту умножить на одну и туже постоянную величину, то средняя:

1. не изменится;

2. увеличится на туже величину;

3. увеличится во столько же раз.

25. Если увеличить каждое значение признака (Х) в 10 раз, то значение средней арифметической взвешенной:

1. не изменится;

2. увеличится на 10 единиц;

3. увеличится в 10 раз;

4. изменение нельзя предсказать.

25. Если увеличить каждое значение признака (Х) на 10 единиц и одновременном уменьшить каждую частоту (f) в 10 раз, то значение средней арифметической взвешенной:

1. не изменится;

2. увеличится на 10 единиц;

3. уменьшится в 10 раз;

4. изменение нельзя предсказать.

25. Если увеличить каждую частоту (f) в 10 раз, то значение средней арифметической взвешенной:

1. не изменится;

2. увеличится на 10 единиц;

3. увеличится в 10 раз;

4. изменение нельзя предсказать.

25. Если увеличить каждую частоту на 50 единиц, то значение средней арифметической взвешенной:

1. не изменится;

2. увеличится на 50 единиц;

3. увеличится в 50 раз;

4. изменение нельзя предсказать.

25. Если увеличить каждое значение признака (Х) на 10 единиц и одновременно увеличить каждую частоту (f) в 10 раз, то значение средней арифметической взвешенной:

1. не изменится;

2. увеличится на 10 единиц;

3. увеличится в 10 раз;

4. увеличится в 100 раз;

5. изменение нельзя предсказать.

25. Если увеличить каждое значение признака (Х) на 10 единиц и одновременно уменьшить каждую частоту (f) в 10 раз, значение средней арифметической взвешенной:

1. не изменится;

2. увеличится на 10 единиц;

3. уменьшится в 10 раз;

4. изменение нельзя предсказать.

25. По результатам зимней и летней сессий средний балл студентов по очной форме обучения составил 4,1 балла, а по заочной форме – 3,2 балла, однако в летнюю сессию доля студентов, обучающихся по заочной форме, снизилась и в результате средний балл успеваемости в летнюю сессию:

1. не изменится;

2. повысился;

3. снизился;

4. результат нельзя предсказать.

25. Если одновременно увеличить каждое значение признака (Х) и каждую частоту (f) на 10 единиц, то значение средней арифметической взвешенной:

1. не изменится;

2. увеличится на 10 единиц;

3. увеличится в 100 раз;

4. изменение нельзя предсказать.

25. Расчет средней арифметической взвешенной производится по формуле:

а)8; b) ; c) ; d) .

25. Расчет средней арифметической простой производится по формуле:

a) ; b) ; c) ; d) .

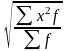25. Расчет средней гармонической взвешенной производится по формуле:

a) ; b) ; c) ; d) .

25. В средней арифметической взвешенной величине частота выражается:

1. числом единиц совокупности в группах;

2. удельным весом;

3. относительной величиной координации;

4. все перечисленное верно.

25. Величина средней арифметической взвешенной зависит от:

1. размера вариант;

2. размера частот;

3. соотношения между частотами.

25. Средняя величина является типичной, если выполняются следующие условия:

1. совокупность качественно однородна;

2. численность совокупности велика;

3. выполняется логическое соотношение между величинами.