3 Примеры расчета

3.1 Пример 1. Расчет сортового валка

Расчетная схема нагружения ручьевого валка приведена на рисунке 2.

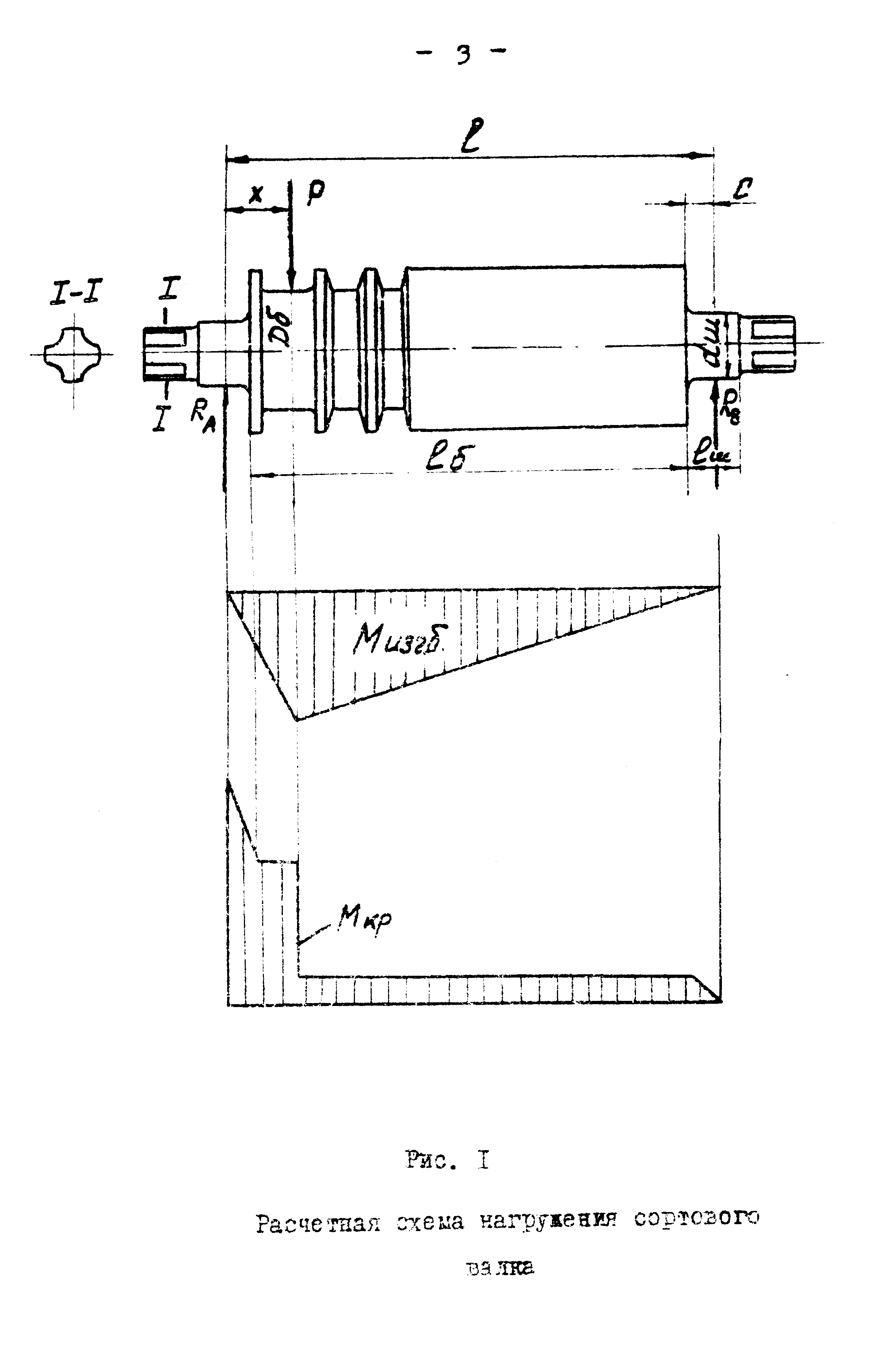
Рисунок 2- Расчетная схема нагружения сортового валка.

Так как при прокатке в разных калибрах величина дав­ления, диаметр бочки и расстояние от оси нажимного винта являются переменными, то необходимо производить расчет напря­жений в бочке и шейке валка для каждого пропуска и в каждом калибре. Из полученных величин выбирается наиболее неблагоприятный случай.

При расчете бочки валка напряжения от кручения обычно не подсчитываются, так как величина их, по сравнению с величиной напряжений от изгиба, намного меньше. Расчет бочки валка производится только на изгиб. При прокатке в любом калибре опорные реакции равны:

R_А = P (ℓ - x) / ℓ, R_B = P x / ℓ. (2)

Изгибающий момент в сечении x (в среднем сечении калибра):

M^δ_изг = P x / ℓ (ℓ – x). (3)

Напряжение изгиба в данном калибре:

б^δ _изг = M ^δ _изг / W_δ, (4)

где W_δ = 0,1D³_δ момент сопротивления поперечного сечения бочки валка на изгиб, см³;

D_δ – диаметр валка в сечении, проходящем по середине ручья, см.

Таким образом ход расчета бочки ручьевого валка таков:

1)определяются изгибающие моменты в середине каждого калибра;

2)строятся эпюры изгибающих моментов (Рисунок 1.);

3)определяются моменты сопротивления сечений каждого калибра;

4)подсчитываются изгибающие моменты для каждого калибра.

Шейка валка рассчитывается на изгиб и кручение.

Изгибающий момент для левой шейки:

M_изг.ш = R_А ℓ_ш / 2; (5)

изгибающий момент для правой шейки:

M_изг.ш = R_В ℓ_ш / 2; (6)

напряжение от изгиба:

б_изг.ш = М_изг.ш / 0,1 d ³_ш (7)

Крутящий момент для приводной шейки

М _кр.ш = М _деф + М _тр, (8)

где М_деф – момент прокатки; М _тр – момент трения в шейках валков.

М _тр = P f_ш d_ш / 2, (9)

где f_ш – коэффициент трения в подшипниках.

Коэффициент трения подшипников:

роликовых 0,002 – 0,005;

текстолитовых 0,004 – 0,006;

бронзовых 0,06 – 0,1;

жидкостного трения 0,001 – 0,005.

Напряжение от кручения

τ _кр.ш = М _кр.ш / 0,2 d ³_ш (10)

Результирующее (приведенное) напряжение для шейки будет равно:

для стальных валков:

б _рез. = √ б ²_изг.ш + 3 τ²_кр - по IV теории прочности (VI т.п.); (11)

для чугунных валков:

б _рез = 0,375 б _изг.ш + 0,625 √ б ²_изг.ш + 4 τ ²_кр - по III т.п. (12)

Пример 2. Выполнить расчет валков блюминга 1300, если дано максимальное давление металла на валки по экспериментальным данным Р = 1400 т.

Размеры валка указаны после максимально допустимой переточки. Валок изготовлен из стали марки 60xн, имеющей предел прочности материала на изгиб б_в = 70 ÷75 кг/мм². При этом допускаемое напряжение равно [б ] = 1400 ÷ 1500 кг/см² .

а) Расчет бочки валка.

1. Определяем опорные реакции на шейках валка

R_А = Р (ℓ - x) / ℓ = 1400 · (3600 – 1015) / 3600 = 1000тн = 1000000кг;

R_В = Р x / ℓ = 1400 · 1015 / 3600 = 400т = 400000кг;

2. Изгибающий момент в среднем сечении калибра

М_изг.δ = R_А · x = 1000000 · 101,5 = 1015 · 10⁵ кгсм;

3. Напряжения изгиба в этом сечении

б_изг.δ = М_изг.δ / 0,1 D³_δ = 1015 · 10⁵ / 0,1 · 102³ = 955 кг/см²

б) Расчет шейки валка.

1. Изгибающий момент для шейки

М_изг.ш = R_А · ℓ_ш /2 = 1000000 · 80 /2 = 200 · 10⁵ кгсм;

2. Напряжения изгиба

б _изг.ш = М _изг.ш / 0,1 d ³_ш = 400 · 10⁵ / 0,1 · 75³ = 1000кг/см² ;

3.Крутящий момент для приводной шейки

М_кр.ш = М_деф + R_А · f_ш · d_ш /2;

М_деф = 16800000 кгсм;

М_тр = 1000 · 10³ · 0,005 · 75 /2 = 188000 кгсм;

М_кр.ш = 16800000 + 188000 = 17000000 кгсм

4. Напряжения кручения

τ _кр.ш = М_кр.ш / 0,2 d³_ш = 17 · 10⁶ / 0,2 · 75³ = 210 кг/см²;

5. Приведенные напряжения в шейке, с учетом совместного действия изгибающего и крутящего моментов (для стальных валков):

б _рез = √ б ²_изг.ш + 3 τ ²_кр.ш = √ 1000² + 3 · 210² = 1050 кг/см²

Полученные значения напряжений как для бочки, так и для шейки не превышают допустимого [ б ] = 1400 + 1500 кг/см².

Пример 3. Расчет листового валка.

Расчетная схема нагружения листового валка приведена на рисунке 3.

Бочка валка рассчитывается на изгиб (опасное сечение 1 – 1), а шейка – на изгиб и кручение (опасное сечение сеч. II – II).

Изгибающий момент:

М_изг.δ = Р · [ ( ℓ_δ + ℓ_ш ) – в/4 ] /4, (13)

где в – ширина листа,

Р – полное давление металла на валки,

б _изг.δ = М_изг.δ / 0.1 D³_δ (14)

Шейка рассчитывается аналогично ручьевого валка, т.е.

М_изг.ш = Р \ 2 · ℓ_ш / 2; б_изг.ш = М_изг.ш / 0,1 d³_ш ; (15)

М_кр.ш = М_деф.+ Р · f_ш · d_ш / 2; τ_кр.ш = М_кр.ш / 0,2 d³_ш (16)

Результирующие напряжения для шейки определяются также, как и для ручьевого валка.

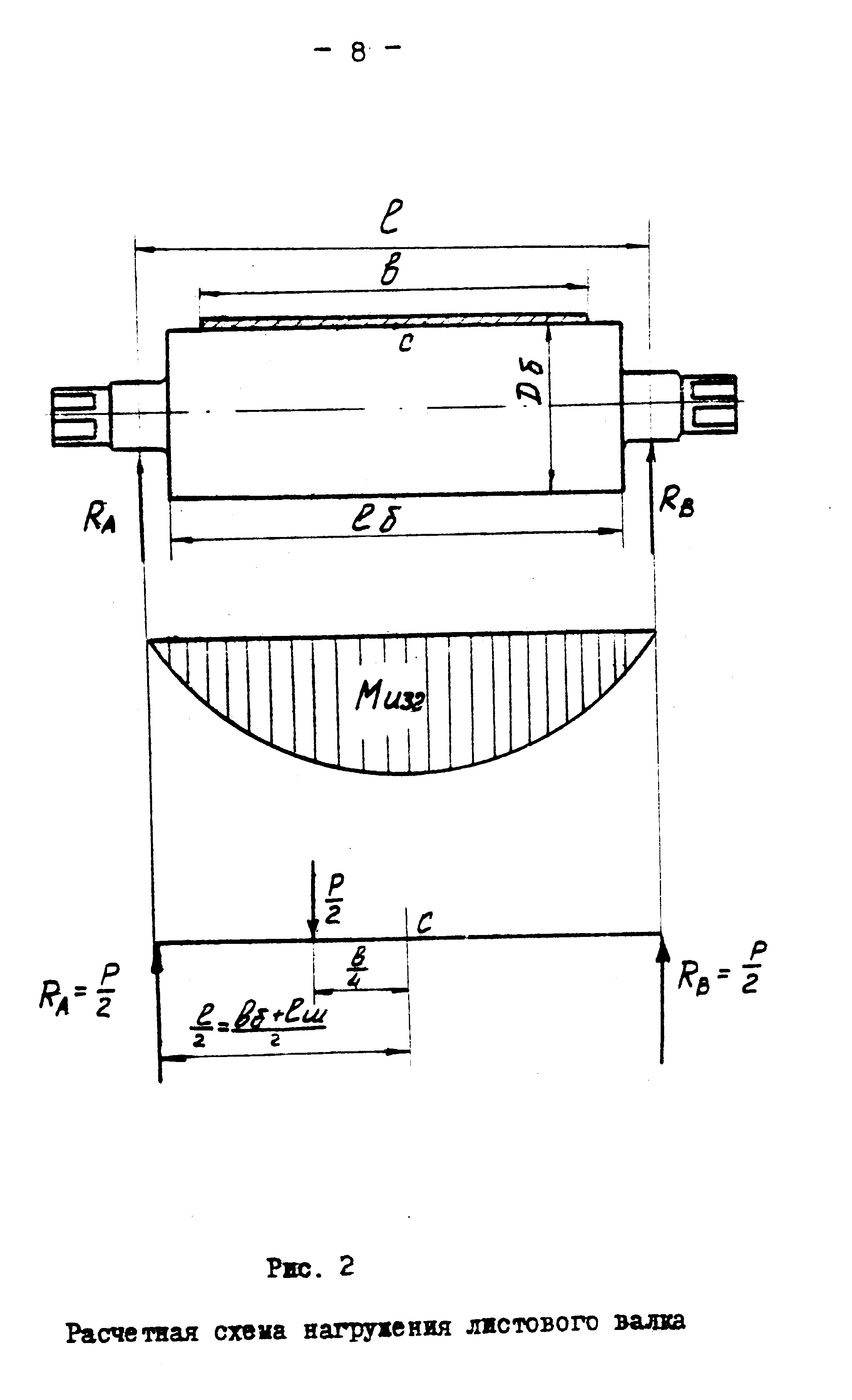
Рисунок 3- Схема нагружения листового валка.

Ниже приводятся допускаемые напряжения на изгиб при пятикратном запасе прочности.

Таблица 10. Допускаемые напряжения на изгиб

№ п/п	Материалы валков.	Допускаемые напряжения, кг/см2
1	Чугунные валки	600 ÷ 800
2	Стальные валки	1000 ÷ 1200
3	Стальные кованые из среднеуглеродистой	1000 ÷ 1200
4	Стальные кованые из низкоуглеродистой	1200 ÷ 1300
5	Стальные кованые из легированной стали	1400 ÷ 1500
6	Легированный чугун	900 ÷ 1000

При расчете величин напряжений следует иметь в виду, что валки в процессе работы подвергаются переточкам. Допускаемая величина переточки:

для блюмингов 10 – 12% (от диаметра нового валка);

для сортовых станов 8 – 10%;

для средне- и толстолистовых 5 - 7%;

для тонколистовых и станов холодной прокатки 3 – 6%.

Пример 4. Расчет приводных концов валков.

Приводные концы рабочих валков могут быть выполнены либо в виде плоской лопасти или в виде трефа. В первом случае расчет их выполняется как и для лопасти шпинделя (см. соответствующий расчет).

Треф валка рассчитывается на кручение. Максимальное напряжение кручения возникает на дне впадин трефа и при

d ₁ = 0,66 d _т равно τ _кр. = М_кр. / 0,07 d ³_т , (17)

где d _т – наружный диаметр трефа;

d ₁ – диаметр вписанной окружности по впадинам трефа.

Допускаемые напряжения: для стали [ τ ] = 800 – 1000 кг/см²;

для чугуна [ τ ] = 700 – 800 кг/см².

Особенности расчета валков у станов кварто.

Рабочие и опорные валки станов кварто выполняют различные функции.

Приводные рабочие валки рассчитываются только на напряжения кручения, а неприводные опорные валки рассчитываются на напряжения изгиба.

Применение опорных валков практически полностью разгружает рабочие валки от действия изгибающих моментов. Распределение напряжений изгиба между опорными и рабочими валками во многом зависит от профилировки валков и реального профиля валков в процессе прокатки.

Обычно верхний рабочий валок имеет выпуклость, а остальные валки изготавливаются цилиндрическими.

Расчеты показывают, что при этом примерно до 97,5% всей нагрузки воспринимается опорным валком, который и рассчитывается на изгиб.

Пример 5. Рассчитать на прочность валки клети кварто тонколистового стана горячей прокатки 1680.

По замерам давление металла на валки равно 1800 тн, а момент про-катки М_пр. = 66 тм.

Размеры валков приведены в таблице 11.

Таблица 11- Размеры валков стана кварто

Валки	Диаметр валков, мм.		z, мм	ℓ, мм	d ш мм	Материал.	Допускаемые напряжения, кг/см2
							изгиба	кручения
Рабочий	610	590	1680	570	395	Легирован. Чугун.	900-1000	350 - 450
Опорный	1240	1170	1680	570	650	Литая сталь.	1000 - 1200

Допускаемое давление металла на валки, исходя из прочности бочки опорного валка.

Р_max.δ = 0,4 · D³_m¡n · R_в / z _δ + ℓ_ш – 0,5 в = 0,4 · 117 · 1100 / 168 + 57 – 0,5 · 150 = 4700000 кг,

где в = 1500мм = 150 см. (ширина прокатываемого листа).

Допускаемое давление, исходя из прочности шейки опорного валка

Р_max.ш = 0,4 · d³_ш · [ б ] / ℓ_ш = 0,4 · 65³ · 1100 / 57 = 2100000 кг.

Таким образом, максимально допустимое давление металла равно

Р_max = 2100т.

Изгибающий момент в опасном сечении бочки опорного валка

М_изг.δ = Р / 2 · (ℓ_ш + z_δ) / 2 – Р / 2 · 0,5в / 2 = Р/4 · (α – в/2);

М_изг.δ = 1800000 / 4 · [ (168 + 57) – 75 ] = 67000000 кгсм;

Изгибающий момент в шейке

М_изг.ш = Р/2 · с.

где с – расстояние от оси нажимного винта до края бочки;

М_изг.ш = 1800000 / 2 · 28,5 = 25000000 кгсм.

Напряжения изгиба

б_δ = М_изг.δ / W_δ = М_изг.δ / 0,1 · D³_δ = 67000000 / 0,1 · 117³ = 425 кг/см² ;

б_ш = М_изг.ш / W_ш = 25000000 / 0,1 · 65³ = 890 кг/см² .

Таким образом, напряжения изгиба не превышают допустимых.

Напряжения кручения в рабочем валке

τ_кр.ш = М_кр.ш / W_кр.ш = М_кр.ш / 0,2 · d³_ш

М_кр.ш = М_пр. / 2 + М_mp.ш = 3300000 + 178000 = 347000кгсм.

М_mp.ш = Р · f_ш · d_ш / 2 = 1800000 · 0,005 · 39,5 \ 2 = 178000кгсм

τ _кр.ш = 3478000 / 0,2 · 39,5³ = 283 кг/см², т.е. не превышает допустимых напряжений для валков из легированного чугуна.

Пример 6. Расчеты валков на усталостную прочность.

Практикой установлено, что многократное приложение нагрузки может вызвать разрушение элементов оборудования при напряжениях, значительно меньших, чем в случае их однократного нагружения. Напряжение, при котором разрушается оборудование, может быть меньше предела прочности и предела текучести, а иногда и предела упругости.

Способность металла выдерживать переменные напряжения называется усталостной прочностью.

Расчеты на статическую прочность валков ведутся по наибольшей кратковременной нагрузке, а на усталостную прочность по наибольшей длительно действующей нагрузке, повторяемость которой за время службы валков не менее 10³ циклов.

Изменение напряжения в любом сечении валка характеризуются циклом, который определяется следующими величинами:

- наибольшее напряжение цикла (с учетом алгебраического знака)

б_max и τ_max ;

- наименьшее напряжение цикла б_min и τ_min;

- среднее напряжение цикла

б_ш = (б_max + б_min) / 2 и τ_m = (τ_max + τ_min) / 2;

- амплитуда цикла

б_α = (б_max - б_min) / 2 и τ_α = (τ_max - τ_min) \ 2;

- коэффициент асимметрии

r = б_min / б_max или r = τ_min / τ_max

При симметричном цикле

r = -1; б_ср. = 0; б_α = б_max = - б_min.

Различные циклы переменного напряжения представлены на рисунке 4.

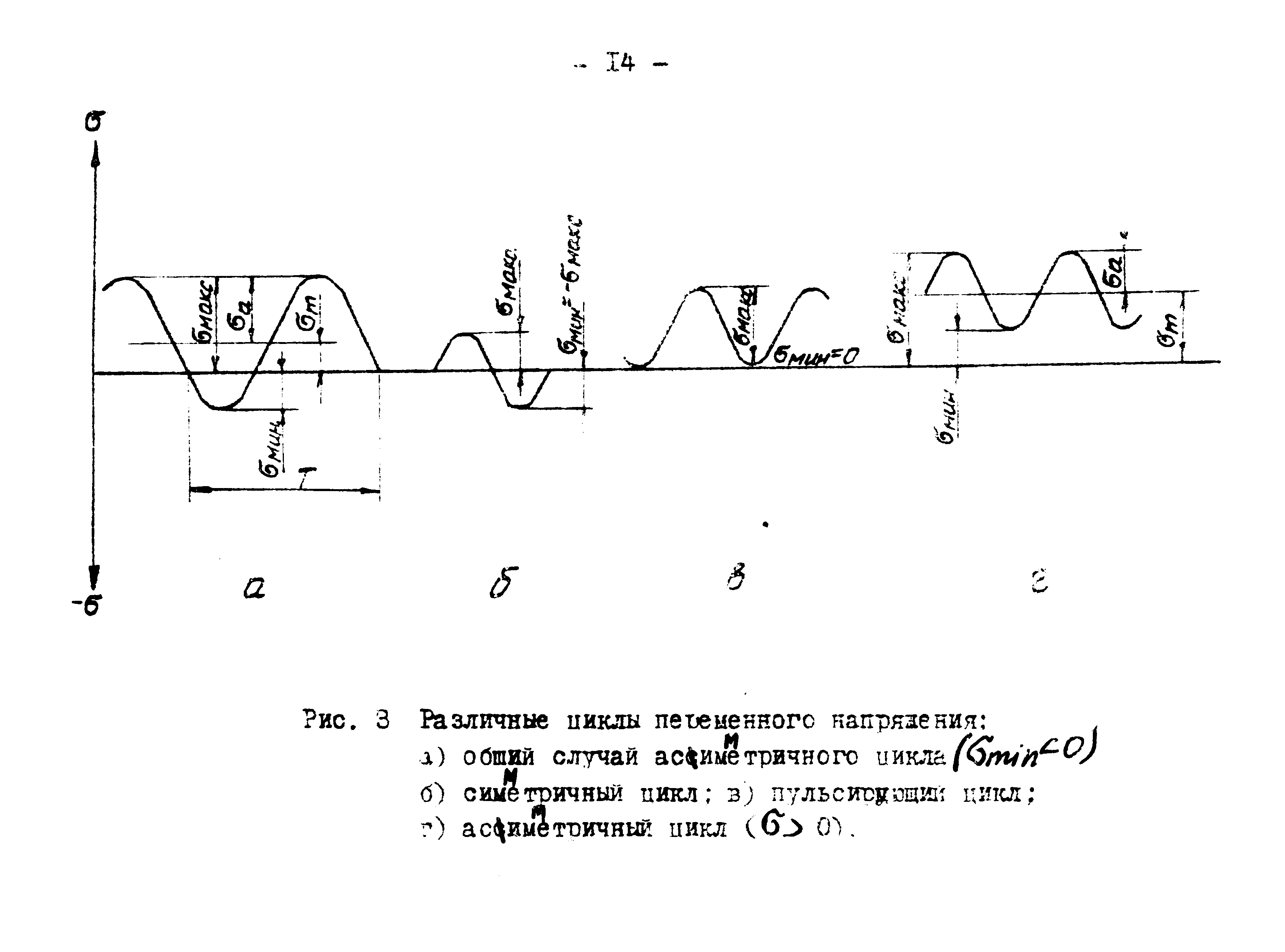
Рисунок 4- Различные циклы переменного напряжения:

а) Общий случай асимметричного цикла (σ_min ‹ 0);

б) симметричный цикл; в) пульсирующий цикл;

г) асимметричный цикл (σ › 0).

Исходными данными при расчетах на усталостную прочность служит значения пределов прочности σ_в, предела текучести σ_т , предела усталости при изгибе σ_-1 и кручении τ_-1 (для симметричного цикла)

б_-1 = (0.45 ÷ 0,55) · б_в (18)

τ_-1 = 0,6 · б_-1 (19)

Значения предела прочности в зависимости от твердости поверхности валков приведены в работе [3, таблица v.6]

Допускаемые напряжения при учете усталостной прочности принимают высокими, исходя из запаса прочности n = 1.1 ÷ 1,4

Запас прочности рассчитывают по формулам [3.]:

а) для бочки валков на изгиб

n = β·ε_б ·б_-1 / б; (20)

б) для шейки опорного валка, работающего только на изгиб

n = β·ε_б · б_-1 / k_б · б , (21)

где β – коэффициент качества поверхности;

ε_{б –} коэффициент влияния абсолютных размеров;

б – максимальное напряжение изгиба, б = М_max / W;

k_б – коэффициент концентрации напряжений;

в) в приводном конце вала запас прочности

n = β·ε_τ · τ_-1 / k_τ · τ (22)

Опорные валки станов кварто работают длительное время без перешлифовок (до 15 – 30 суток). Для деталей машин, подвергающихся в процессе длительной эксплуатации многократным переменным нагрузкам, величина допустимой нагрузки недостаточна для характеристики прочностных свойств. Поэтому необходимо воспользоваться эксперимен-тальными данными приведенных в [3, с. 190 – 220].

Расчеты опорных валков на усталостную прочность показывают, что наиболее опасным сечением, является граница между бочкой и шейкой валка (сеч. ІІ-ІІ Рисунок 8). Для этого сечения и производится определение допускаемого напряжения по условиям усталостной прочности.

Для валков прокатных станов, напряжения изгиба в которых меняются по симметричному циклу, допускаемое напряжение определяется по формуле

[ б ]_доп. = б_-1 · ε_б · β / k_б · n (23)

где k_б – коэффициент концентрации напряжений при изгибе;

n – принятый коэффициент запаса прочности.

Принимаем б_-1 = 0,45 · б_в = 0,45 · 80 = 36 кг/мм²

Коэффициент β определяем по кривой 2 (Рисунок 5).

При б_в = 80 кг/мм², коэффициент β = 0,90.

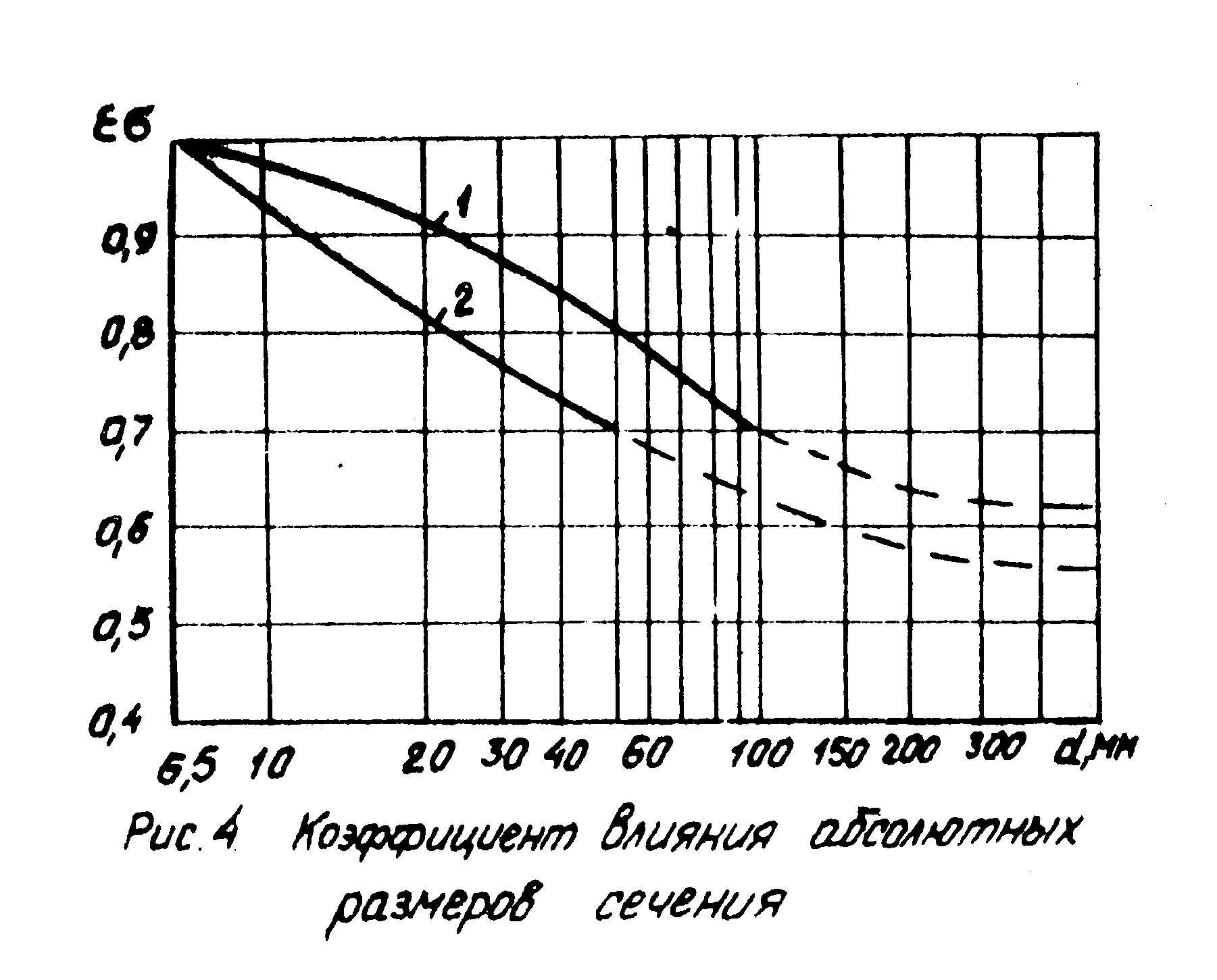
Рисунок 5- Коэффициент влияния абсолютных размеров сечения ε_σ

Коэффициент ε_б определяем по кривой 2 (Рисунок 4). Экстраполируя, находим для d_ш = 850мм; ε_б = 0,515.

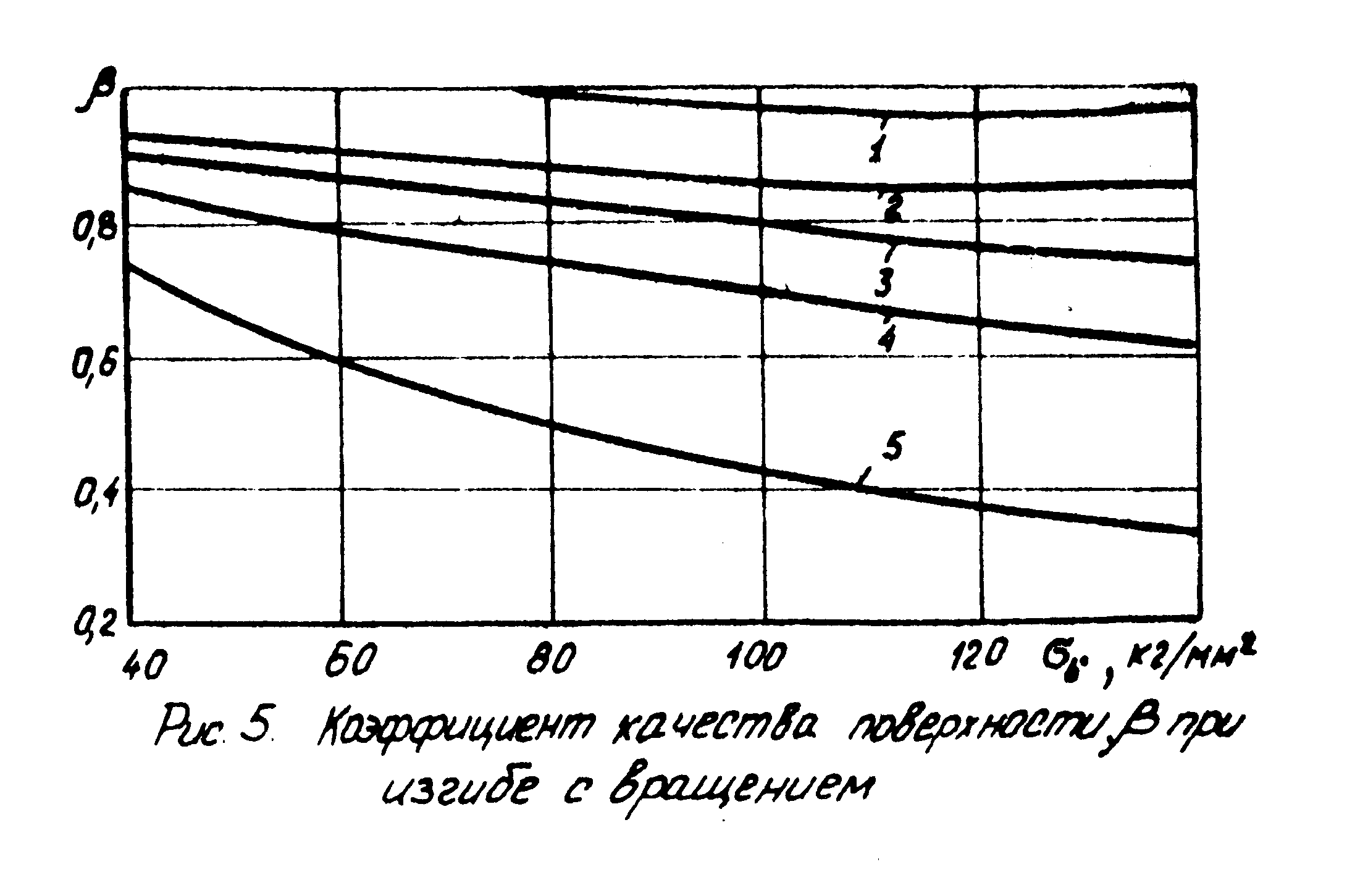
Рисунок 6-Зависимость коэффициента качества поверхности β от способа механической обработки: 1 – полирование; 2 – тонкое шлифование; 3 – тонкое обтачивание; 4 – грубое обтачивание; 5 – необработанная .

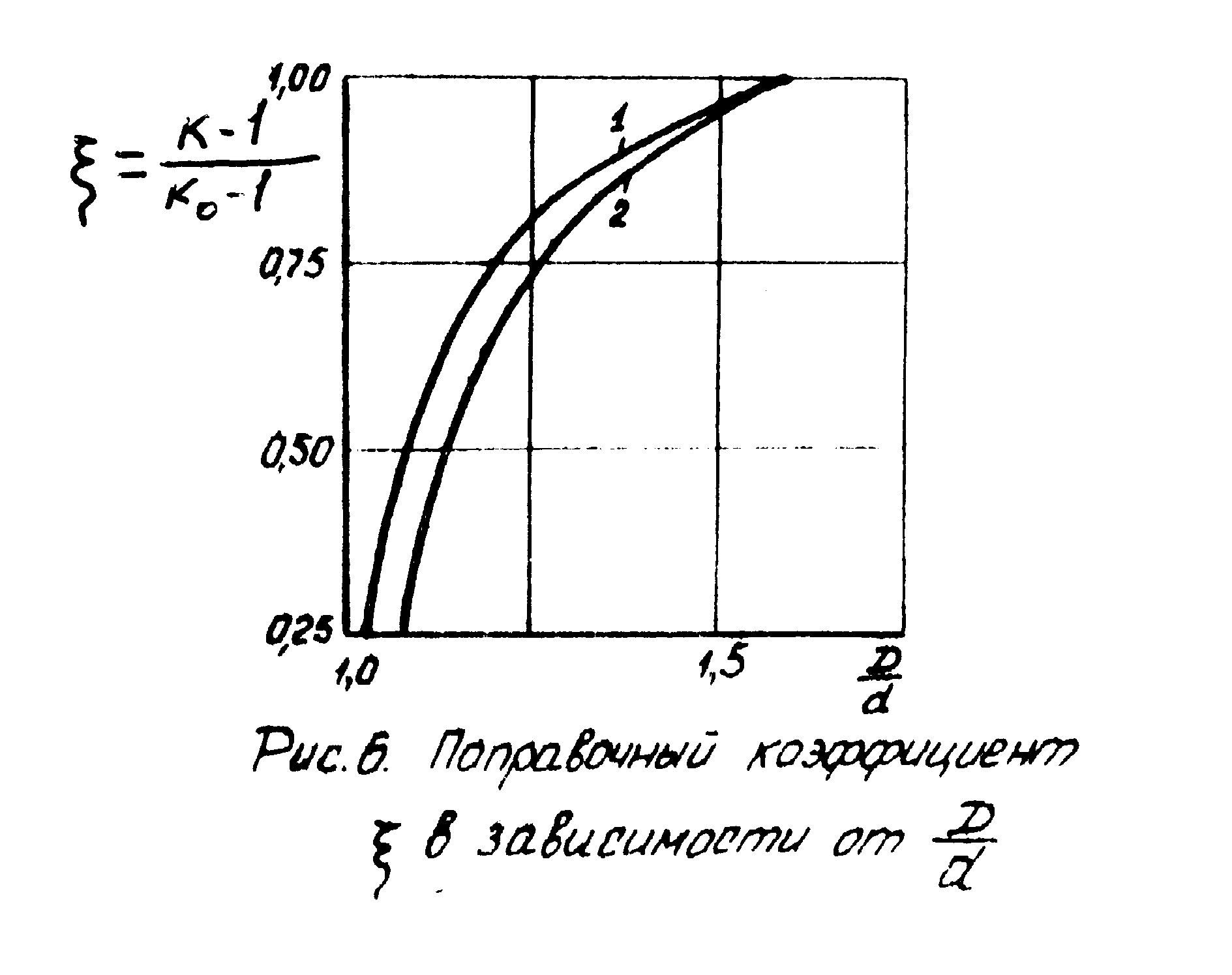
Рисунок 7- Поправочный коэффициент ξ в зависимости от отношения D/d.

где ξ – поправочный коэффициент, определяемый по кривой I (Рисунок 6).

Для D / d = 1,5; ξ = 0,975.

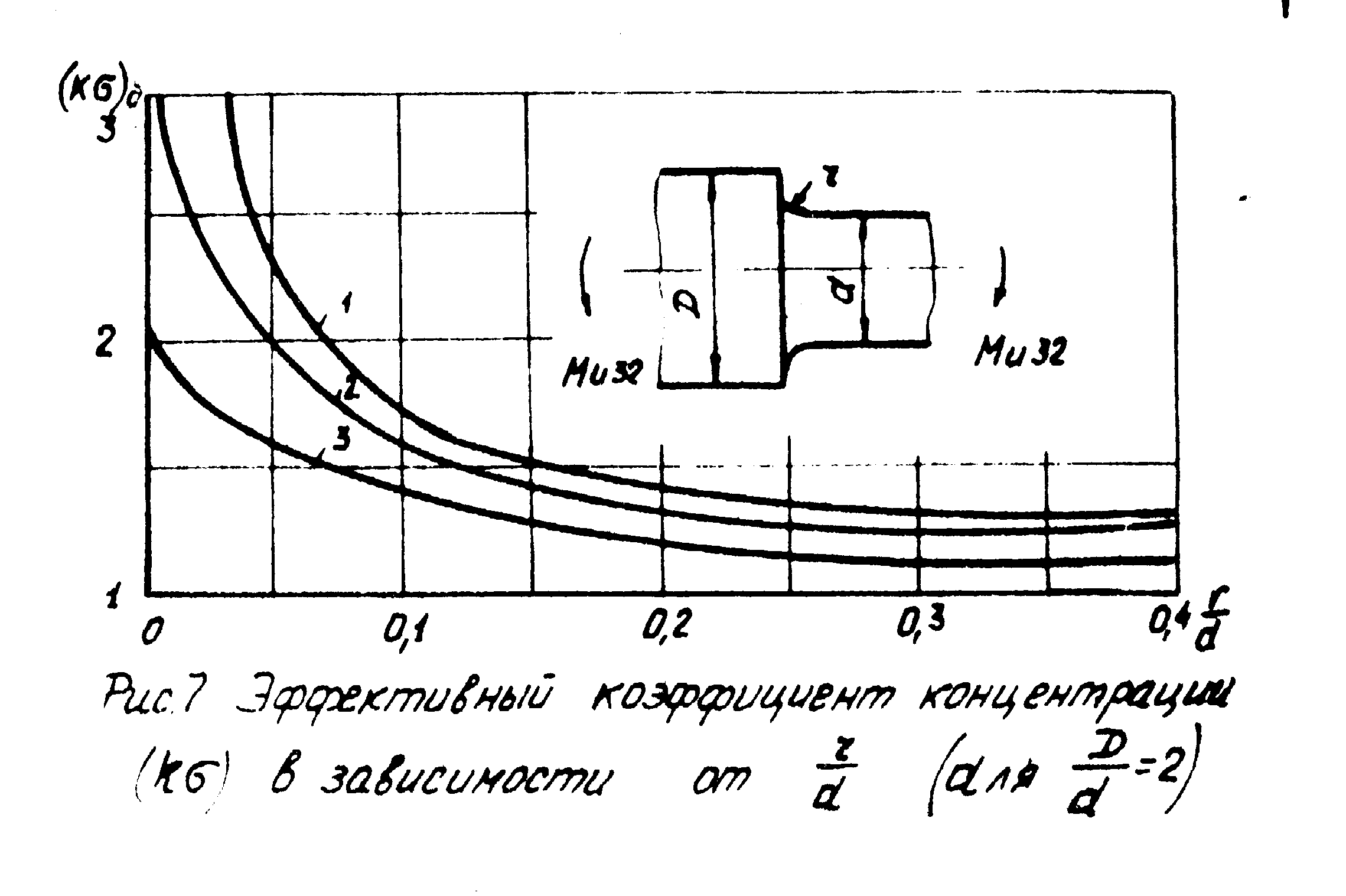
Рисунок 8- k_б)_D – эффективный коэффициент концентрации напряжений.

(k_б)_D находим по кривой I (Рисунок 8 при r / d = 85 / 850 = 0,1; находим (k_б)_D = 1,5.

k_σ = 1 + ξ[(k_σ)_D – 1], (24)

Тогда, k_б = 1 + 0,975 · (1,5 - 1,0) = 1,60

Коэффициент запаса прочности для стальных валков рекомендуется принимать равным: n = 1,1 ÷1,4

Допускаемое напряжение из условий усталостной прочности при изгибе (при n = 1,3):

[ б ]_доп = 36,0 · 0,515 · 0.90 / 1,6 · 1,3 = 7,90 кг/см² , т.е.

[б]_доп = 790 кг/мм²

Максимально допустимое давление металла на валки по условиям усталостной прочности

Р^уст_доп = 0,2 · d³_ш · [б]_доп / в = 0,2 · 85³ · 790 / 59 = 1650000 кг,

Р^уст_доп = 1650т.

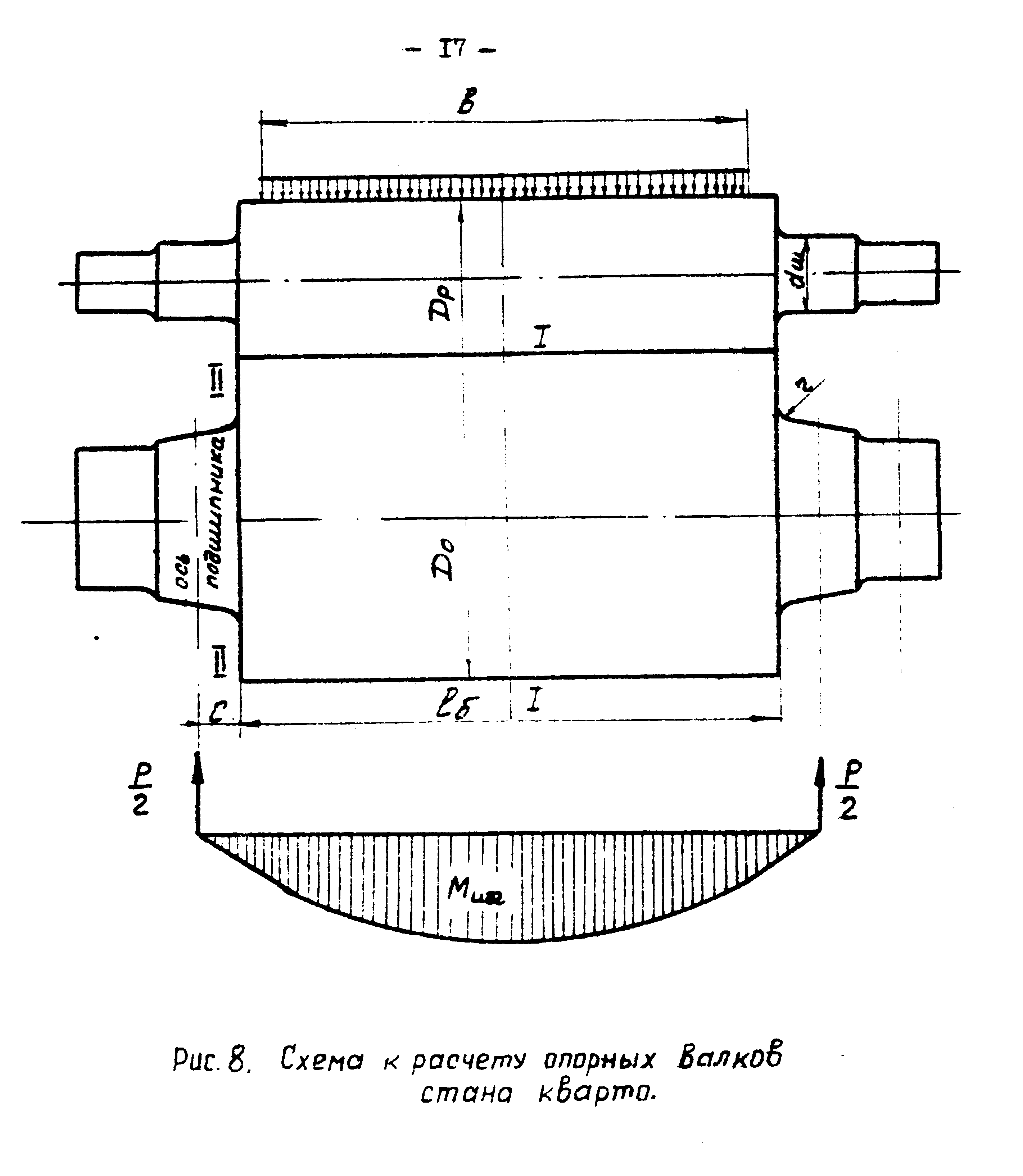
Рисунок 9-Схема к расчету опорных валков стана кварто.

Пример 7. Расчет упругой деформации валков.

Прогиб рабочих и опорных валков оказывает влияние главным образом на форму поперечного сечения полосы и практически не влияет на величину упругой деформации клети.

Сближение центров валков происходит в результате упругого сплющивания рабочих и опорных валков, под действием большого погонного давления (Рисунок 9).

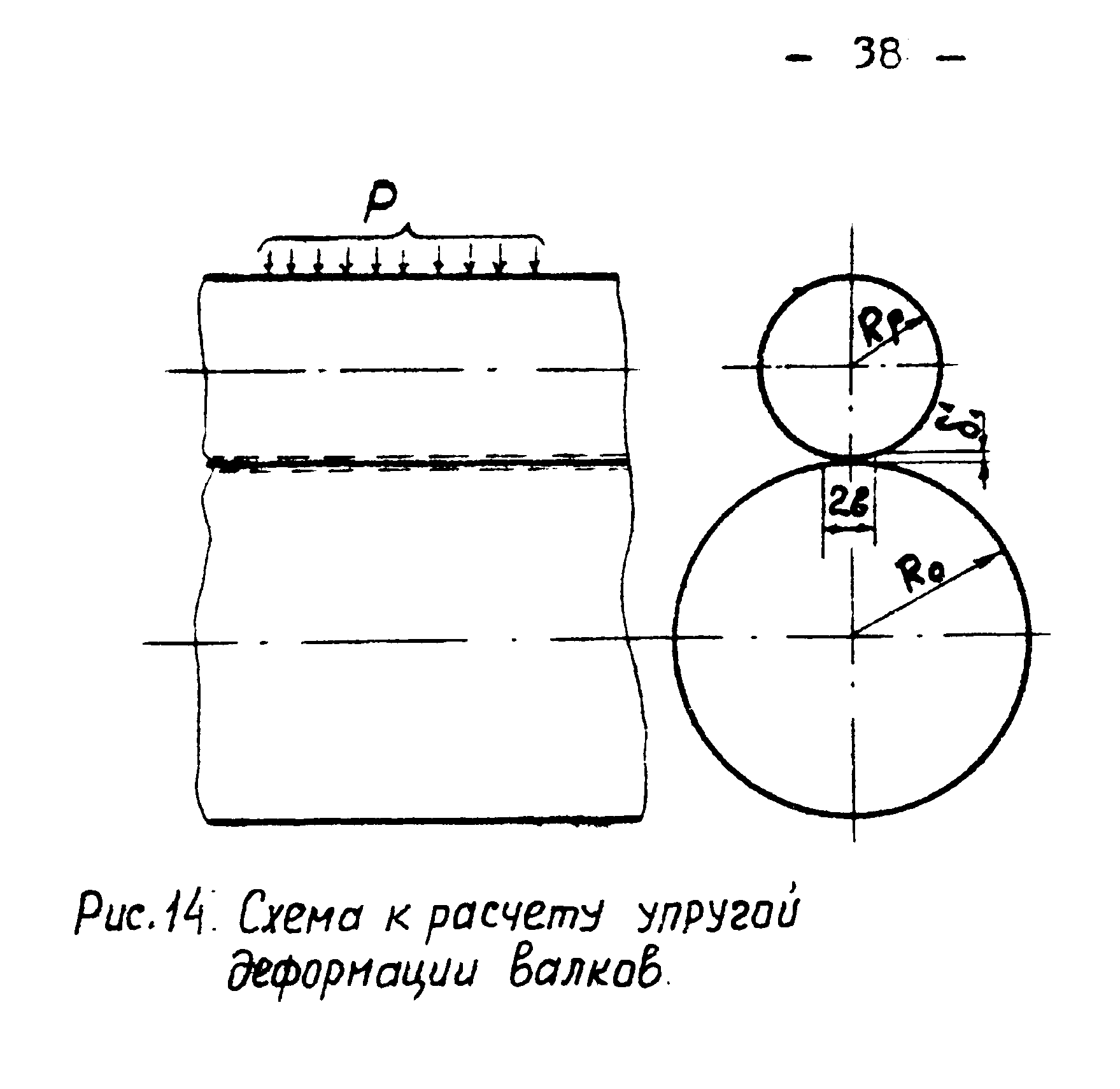
Рисунок 9-Схема к расчету упругой деформации валков.

На основе теории Герца величина сближения центров двух цилиндров из одинакового материала определяется формулой:

δ^΄₁ = 1,3 · Р / Е ·ℓ · ℓq[35,5 · Е ·ℓ / (1/R_р – 1/R_D) · Р] , (25)

где Е – модуль упругости;

Р – давление металла на валки;

ℓ - длина бочки валков;

R_D и R_р – радиусы опорного и рабочего валков.

δ^΄₁ = 1,3·5·10⁵/2,·10⁶·145 ℓq [35,5·2,1·10⁶·145 / (1/25+1/56,5)·5 · 10⁵] = 0,0119 см.

Контактное сжатие происходит в двух парах валков, в связи с чем суммарная деформация валков равна

δ ₁ = 2δ^΄₁ = 2 · 0,119 = 0,238 мм.

Рекомендуемая литература

Основная литература

1. Технология прокатного производства. В 2 – х книгах . Кн. 1. Справочник: Беняковский М.А., Богоявленский К.Н., Виткин А.И. и др. М. Металлургия, 1991 г., 440 с.

2. Технология прокатного производства. В 2 – х книгах . Кн. 2. Справочник: Беняковский М.А., Богоявленский К.Н., Виткин А.И. и др. М. Металлургия, 1991 г., 423 с.

3. Королев А.А. Конструкция и расчет машин и механизмов прокатных станов. Учеб. пособие для вузов, 2-е изд., испр. и доп.– М.: Металлургия, 1985, 376с.

4. Королев А.А. Конструкция и расчет машин и механизмов прокатных станов. Учеб. пособие для вузов– М.: Металлургия, 1969, 464с.

5. Машины и агрегаты металлургических заводов. В 3 – х томах. Т. 3. Машины и агрегаты для производства и отделки проката. Учебник для вузов/ Целиков А.И., Полухин П.И., Гребенник В.М. и др. 2-е изд., перераб. И доп. – М.: Металлургия, 1988. 680 с.

6. Машиностроение. Энциклопедия в 40 томах. Том IV-5 Машины и агрегаты металлургического производства. – М.: Машиностроение, 2004 – 912 с.

Дополнительная литература

1. Прокатное производство. П.И. Полухин, И.М. Федосов, А.А. Кор-

олев, Ю.М. Матвеев. – 3 – е изд., перераб. и доп. – М.: Металлургия, 1982. – 696 с.

2. Чекмарев А.П., Мутьев В.С., Машковцев Р.А. Калибровка прокат-

ных валков. – М.: Металлургия, 1971. – 508 с.

3. Жадан В.Т., Осадчий А.Н., Стеценко Н.В. Отделка и термическая обработка сортового проката. – М.: Металлургия, 1978. – 192 с.

4. Коновалов Ю.В., Остапенко А.П., Понамарев В.И. Расчет параметров листовой прокатки: Справочник. – М.: Металлургия, 1986. – 430 с.

5. Давильбеков Н.Х. Оборудование прокатных цехов (Учебник). – Алматы: КазНТУ, 2002. – 243 с.

24