Министерство высшего образования РФ

Санкт-Петербургский Государственный Политехнический Институт

Электромеханический факультет

Кафедра “Электрические системы и сети”

Курсовая работа

“Математические задачи энергетики”

Вариант 11

Выполнил студент

группы 3023/1

Кожевников А.

Преподаватель:

Беляев А. Н.

Санкт-Петербург

2010 год

1. Цифровое описание расчётной схемы.

Расчётная схема:

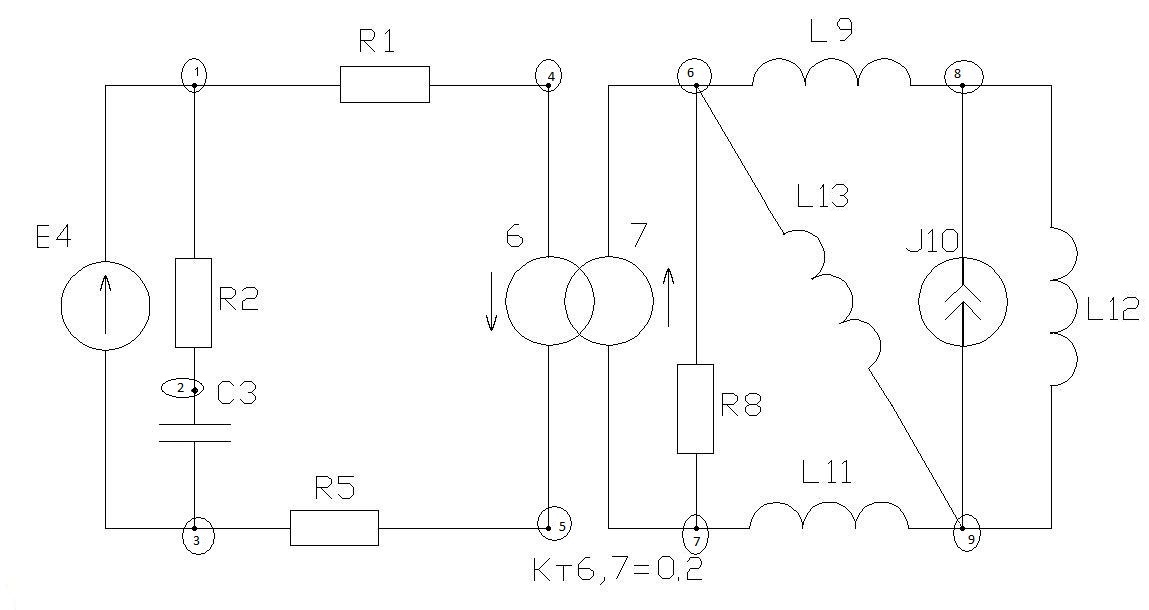
Граф расчётной схемы:

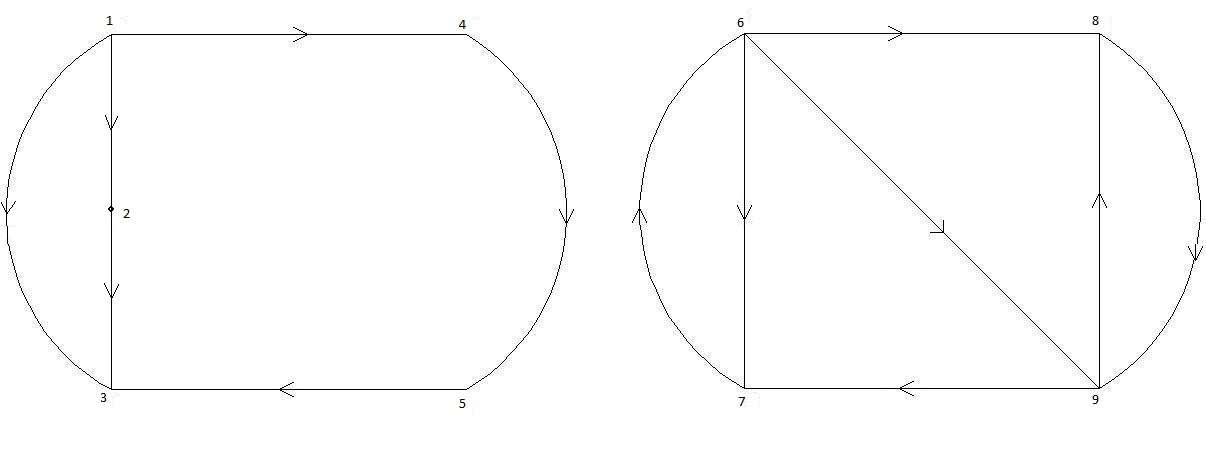
Цифровое описание вершин графа:

От вершине 1 и отходят 2-е, 1-е и 4-е рёбра. Таким образом

λ₁ = [-1-2-4]

Аналогично:

λ₂ = [+2-3]

λ₃ = [+3+4+5]

λ₄ = [+1-6]

λ₅ = [-5+6]

λ₆ = [+7-8-9-13]

λ₇ = [-7+8+11]

λ₈ = [+9+10-12]

λ₉ = [-10-11+12+13]

Цифровое описание конфигурации расчётной схемы (совокупность структурно ориентированных чисел λ):

Λ_К = [-1-2-4] [+2-3] [+3+4+5] [+1-6] [-5+6] [+7-8-9-13] [-7+8+11] [+9+10-12] [-10-11+12+13]

Типы ветвей:

Ψ₁ = {Ø} (ЗК-тип - замкнутые ключи)

Ψ₂ = {4} (Е-тип - источники ЭДС)

Ψ₃ = {3} (С-тип - конденсаторы)

Ψ₄ = {1,2,5,8} (R-тип – резисторы)

Ψ₅ = {9,11,12,13} (L-тип – катушки индуктивности)

Ψ₆ = {10} (J-тип – источники тока)

Ψ₇ = {Ø} (РК-тип – разомкнутые ключи)

Ψ₈ = {6,7} (идеальный трансформатор К_6,7 = 0.2)

2. Определение компонент орграфа и получение неизбыточного цифрового описания конфигурации расчётной схемы.

Определение непосредственных связей (алгоритм НС):

Исходные данные:

Λ_К = [-1-2-4] [+2-3] [+3+4+5] [+1-6] [-5+6] [+7-8-9-13] [-7+8+11] [+9+10-12] [-10-11+12+13]

1. Выделить первое с.о.ч. λ из совокупности Λ_К: [-1-2-4]

2. Занести порядковый номер i числа λ в список η₁: η₁ = {1}

3. Выделить идентификатор первого элемента из числа λ_i: 1

4. Среди остальных чисел совокупности Λ_К установить такие, которые содержат элементы с выделенным идентификатором. Порядковые номера этих чисел занести в η_1, не допуская повторений: η₁={1,2}

5. Повторить п. 4 для всех остальных идентификаторов с.о.ч. λ_i и получить последовательность η₁ окончательного состава: η₁={1,2,3,4}

Выполнение последующих циклов алгоритма для всех λ даёт:

η₂={2,1,3} η₅={5,3,4} η₈={8,6,9}

η₃={3,1,2,5} η₆={6,7,8,9} η₉={9,6,7,8}

η₄={4,1,5} η₇={7,6,9}

Определение числа компонент связности графа (алгоритм КС):

Исходные данные:

η₁={1,2,3,4} η₅={5,3,4} η₉={9,6,7,8}

η₂={2,1,3} η₆={6,7,8,9}

η₃={3,1,2,5} η₇={7,6,9}

η₄={4,1,5} η₈={8,6,9}

_____________________________________________________________________

1. Образовать из всех списков η_i (i = 1..n) последовательность H:

Н: {1,2,3,4},{2,1,3},{3,1,2,5},{4,1,5},{5,3,4},{6,7,8,9},{7,6,9},{8,6,9},{9,6,7,8}

Присвоить начальное значение номеру компоненты связности: j = 1. Положить x_j = {Ø}

2. Выделить первый список из последовательности Н. Элементы этого списка занести в x_j, а сам выделенный список удалить из последовательности Н:

x_j = {1,2,3,4}

Н: {2,1,3},{3,1,2,5},{4,1,5},{5,3,4},{6,7,8,9},{7,6,9},{8,6,9},{9,6,7,8}

3. Выделить второй элемент списка x_j: 2

4. Выделенный элемент обозначить a_m: a_m = 2

5. Среди оставшихся списков последовательности Н найти тот, первый элемент которого совпадает с a_m. Дополнить x_j элементами этого списка, не допуская повторений, а сам список исключить из последовательности Н:

x_j = {1,2,3,4}

Н: {3,1,2,5},{4,1,5},{5,3,4},{6,7,8,9},{7,6,9},{8,6,9},{9,6,7,8}

6. Повторить пп. 3-5 для последующих элементов списка x_j. Получим:

x_j = {1,2,3,4,5}

Н: {5,3,4},{6,7,8,9},{7,6,9},{8,6,9},{9,6,7,8}

7. Если в последовательности Н есть списки, присвоить номер компоненты связности j = j+1 и присвоить x_j = {Ø}. Повторить пп. 2-6 для оставшихся списков в последовательности Н. Окончательно получим две компоненты связности:

x₁ = {1,2,3,4,5}

x₂ = {6,7,8.9}

Таким образом, граф расчётной схемы имеет две компоненты связности, которые описываются с.о.ч. совокупности Λ_К с порядковыми номерами соответственно 1,2,3,4,5 и 6,7,8,9. Исключив из каждого из этих списков по одному элементу получим неизбыточное цифровое описание графа расчётной схемы в виде совокупности с.о.ч. Λ_К:

Λ_К = [-1-2-4] [+2-3] [+3+4+5] [-5+6] [-7+8+11] [+9+10-12] [-10-11+12+13]