60.Вихревое электрическое поле.

Из закона Фарадея ξ=dФ/dt следует, что любое изменение сцепленного с контуром потока магнитной индукции приводит к возникновению элек­тродвижущей силы индукции и вследствие этого появляется индукционный ток. Сле­довательно, возникновение э.д.с. электро­магнитной индукции возможно и в непод­вижном контуре, находящемся в перемен­ном магнитном поле. Однако э.д.с. в любой цепи возникает только тогда, когда в ней на носители тока действуют сторонние силы — силы неэлектростатического про­исхождения. Поэтому возника­ет вопрос о природе сторонних сил в дан­ном случае.

Опыт показывает, что эти сторонние силы не связаны ни с тепловыми, ни с хи­мическими процессами в контуре; их воз­никновение также нельзя объяснить сила­ми Лоренца, так как они на неподвижные заряды не действуют. Максвелл высказал гипотезу, что всякое переменное магнит­ное поле возбуждает в окружающем про­странстве электрическое поле, которое и является причиной возникновения ин­дукционного тока в контуре. Согласно представлениям Максвелла, контур, в ко­тором появляется э.д.с., играет второсте­пенную роль, являясь своего рода лишь «прибором», обнаруживающим это поле.

Итак, по Максвеллу, изменяющееся во времени магнитное поле порождает элек­трическое поле Е_B, циркуляция которого, где E_Bl — проекция вектора E_B на направ­ление dl.

Подставив в формулу выраже­ние , получим . Если поверхность и контур неподвиж­ны, то операции дифференцирования и ин­тегрирования можно поменять местами. Следовательно, где символ частной производной подчерки­вает тот факт, что интеграл является функцией только от времени.

циркуляция вектора напряженности электростатического поля вдоль любого замкну­того контура равна нулю:

Сравнивая выражения, видим, что между рассматриваемыми по­лями (Е_B и e_q) имеется принципиальное различие: циркуляция вектора Е_B в отли­чие от циркуляции вектора e_q не равна нулю. Следовательно, электрическое поле Е_B, возбуждаемое магнитным полем, как и само магнитное поле, явля­ется вихревым.

61.Ток смещения.

Р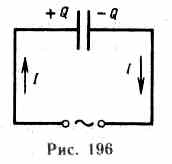 ассмотрим цепь переменного тока, содержащую конденсатор. Между обкладками заряжающегося и разряжающегося конденсатора имеется переменное электрическое поле, поэтому, согласно Максвеллу, через конденсатор «протекают» токи смещения, причем в тех участках, где отсутствуют проводники.

Найдем количественную связь между изменяющимся электрическим и вызывае­мым им магнитным полями. По Максвел­лу, переменное электрическое поле в кон­денсаторе в каждый момент времени со­здает такое магнитное поле, как если бы между обкладками конденсатора су­ществовал ток проводимости, равный току в подводящих проводах. Тогда можно утвер­ждать, что токи проводимости (I) и сме­щения (I_см) равны: I_см=I. Ток проводи­мости вблизи обкладок конденсатора (поверхностная плотность заряда  на обкладках равна электрическому смещению D в конденсаторе.

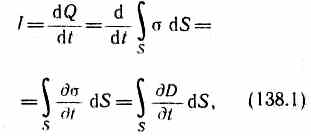
Подынтегральное выражение можно рас­сматривать как частный случай скалярного произведения (дD/дt)dS, когда дD/дt и dS взаимно параллельны. Поэтому для обще­го случая можно записать

Сравнивая это выражение с I=I_см = , имеем (1) Выражение (1) и было названо Мак­свеллом плотностью тока смещения.

Подчеркнем, что из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно — способность создавать в окружаю­щем пространстве магнитное поле. Таким образом, ток смещения (в вакууме или веществе) создает в окружающем про­странстве магнитное поле.

В диэлектриках ток смещения состоит из двух слагаемых. Так как, D=₀E+P, где Е — напряжен­ность электростатического поля, а Р — поляризованность, то плотность тока смещения где ₀дE/дt — плотность тока смещения в вакууме, дP/дt — плотность тока поляри­зации — тока, обусловленного упорядо­ченным движением электрических зарядов в диэлектрике. Возбуждение магнитного поля токами поляризации пра­вомерно, так как токи поляризации по своей природе не отличаются от токов проводимости.

Максвелл ввел понятие полного тока, равного сумме токов проводимости (а так­же конвекционных токов) и смещения. Плотность полного тока j_полн=j+дD/дt. Введя понятия тока смещения и полного тока, Максвелл по-новому подошел к рас­смотрению замкнутости цепей переменного тока. Полный ток в них всегда замкнут, т. е. на концах проводника обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости.

Максвелл обобщил теорему о циркуля­ции вектора Н, введя в ее правую часть полный ток I_полн= сквозь поверхность S, натянутую на замк­нутый контур L. Тогда обобщенная теоре­ма о циркуляции вектора Н запишется в виде

62.Уравнения Максвелла для электромагнитного поля.

В основе теории Максвелла лежат рас­смотренные четыре уравнения:

1. Электрическое поле мо­жет быть как потенциальным (e_q), так и вихревым (Е_B), поэтому напряженность суммарного поля Е=Е_Q+Е_B. Так как циркуляция вектора e_q равна нулю, а циркуляция вектора Е_B оп­ределяется выражением , то цир­куляция вектора напряженности суммар­ного поля Это уравнение показывает, что источни­ками электрического поля могут быть не только электрические заряды, но и меняю­щиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора Н: Это уравнение показывает, что магнит­ные поля могут возбуждаться либо дви­жущимися зарядами, либо переменными электрическими полями.

3. Теорема Гаусса для поля D: Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плот­ностью , то формула запишется в виде

4. Теорема Гаусса для поля В: Итак, полная система уравнений Максвел­ла в интегральной форме: 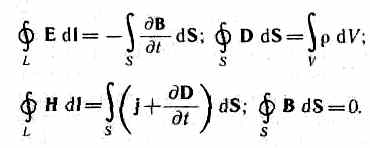Величины, входящие в уравнения Мак­свелла, не являются независимыми и меж­ду ними существует следующая связь: D=₀E, В=₀Н, j=E, где ₀ и ₀ — соответственно электриче­ская и магнитная постоянные,  и  — соответственно диэлектрическая и магнит­ная проницаемости,  — удельная прово­димость вещества.

Для стационарных полей (Е=const и В=const) уравнения Максвелла при­мут вид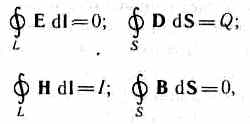 т. е. источниками электрического поля в данном случае являются только электри­ческие заряды, источниками магнитно­го — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электриче­ское и магнитное поля.

В оспользовавшись известными из векторного анализа теоремами Стокса и Гаусса можно представить полную систему урав­нений Максвелла в дифференциальной форме:

Уравнения Максвелла — наиболее об­щие уравнения для электрических и маг­нитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в ме­ханике. Из уравнений Максвелла следует, что переменное магнитное поле всегда свя­зано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнит­ным, т. е. электрическое и магнитное поля неразрывно связаны друг с другом — они образуют единое электромагнитное поле.

63.Свободные гармонические колебания в колебательном контуре.

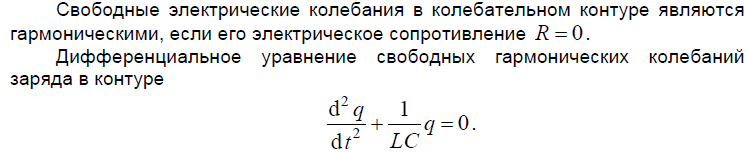
64.Свободные затухающие колебания в колебательном контуре. Коэффициент затухания, логарифмический декремент, добротность контура.

Свободные затухающие колебания в колебательном контуре обусловлены перехо-дом электрической энергии конденсатора в магнитную энергию индуктивности и в виде тепловой потери.

Дифференциальное управление затухающих свободных ко-лебаний в электрическом контуре имеет вид:

(7.1)

где – заряд на обкладках конденсатора .

Решение уравнения (7.1) имеет вид: (7.2) где – начальный заряд на обкладках конденсатора; – коэффициент затухания;

– циклическая частота затухающих колебаний;

– частота собственных колебаний контура;

– начальная фаза колебаний.

Напряжение на обкладках конденсатора изменяется со временем по аналогичному закону, т.к. .

(7.3) где .

Амплитуда колебательного процесса убывает со временем по экспоненте (рис.7.1).

Для возникновения в контуре свободных затухающих колебаний необходимо выполнение условий: . (7.4)

При этом

или (7.5)

Если , то процесс разряда конденсатора в конту-ре перестает быть колебательным и становится апериоди-ческим (рис. 7.1,б).

Сопротивление, при превышении которого в контуре не возникают периодические колебания, называется критичес-ким и определяется из условия: . (7.6)

Количественной характеристикой затухающих колебаний является логарифмический декремент затухания, который определяется как натуральный логарифм отношения ампли-туд, вычисленных через период: (7.7)

Для большей точности при проведении экспериментов удобнее сравнивать амплитуды, отстоящие друг от друга не на один, а на периодов (например, на рис.7.1,а ). Легко убедиться, что в этом случае (7.8)

Логарифмический декремент затухания можно опреде-лить как величину, обратную числу колебаний, после кото-рых амплитуда уменьшается относительно значения в раз.

Для характеристики затухания колебательно контура поль-зуются также величиной, называемой добротностью: (7.9)

Добротностью контура тем выше, чем меньше затухания в нем.

В радиотехнических устройствах (радиоприемники, пе-редатчики и другие) важной характеристикой является ши-рина полосы пропускания или избирательность контура. Чем больше добротность, тем уже полоса пропускания и, соот-ветственно, выше избирательность и помехозащищенность устройств.