Силы, действующие на заряд в диэлектрике

Если в электрическое поле в вакууме внести заряженное тело таких размеров, что внешнее поле в пределах тела можно считать однородным (в этом случае тело можно рассматривать как точечный заряд), то на тело будет действовать сила

Ч тобы заряженное тело поместить в поле, созданное в диэлектрике, в последнем нужно сделать полость. В жидком или газообразном диэлектрике такую полость образует само тело, вытесняя диэлектрик из занимаемого им объема. На поверхности полости возникают связанные заряды, поэтому поле внутри полости будет отлично от поля Е в сплошном диэлектрике. Таким образом, силу, действующую на помещенное в полость заряженное тело, нельзя вычислять как произведение заряда q на напряженность поля Е.Вычисляя силу, действующую на заряженное тело в жидком или газообразном диэлектрике, нужно учитывать еще одно обстоятельство. При поляризации диэлектрики слегка деформируются. Это явление называется электрострикцией. Из-за электрострикции на границе с телом в диэлектрике возникают механические натяжения, что приводит к появлению дополнительной механической силы, действующей на тело. В случае полости в твердом диэлектрике подобная сила, естественно, не возникает.

Для силы взаимодействия двух точечных зарядов, погруженных в однородный безграничный) диэлектрик, можно написать

Д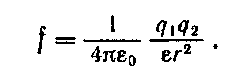 анная формула выражает закон Кулона для зарядов, находящихся в диэлектрике. Она применила только для жидких и газообразных диэлектриков.

Теперь найдем силу, действующую на точечный заряд, помещенный в полость внутри твердого диэлектрика. Рассмотрим несколько случаев.

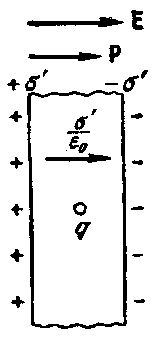
Узкая поперечная щель. Сделаем в однородно поляризованном диэлектрике полость в виде узкой щели, перпендикулярной к векторам Е и Р. На поверхностях диэлектрика, ограничивающих щель, возникнут связанные заряды, плотность которых σ' — Р. В середине щели они создадут дополнительное поле напряженности

н аправленное так же, как и поле Е в сплошном диэлектрике. Следовательно, напряженность поля в середине щели равна E = P/ε₀. Эта величина совпадает с D/ε₀ в диэлектрике. Таким образом, сила, действующая на заряд, помещенный в середине узкой поперечной щели, равна

Узкая продольная полость. Если полость в диэлектрике имеет вид узкого длинного цилиндра с образующими, параллельными векторам Е и Р, напряженность поля в ее середине будет такой же, как в сплошном диэлектрике. Это объясняется тем, что связанные заряды, возникающие на торцах полости, малы по величине (мала площадь торца) и далеко отстоят от середины полости, поэтому создаваемое ими дополнительное поле пренебрежимо мало. Сила, действующая на заряд, помещенный в середине узкой продольной полости, равна qE.

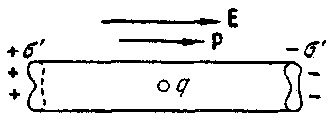
Полость сферической формы. Вычислим напряженность дополнительного поля в центре сферической полости радиуса R. Нормальная составляющая вектора поляризации для разных точек поверхности полости изменяется в пределах от Р до нуля. Соответственно изменяется и плотность связанных зарядов σ'.

Будем характеризовать точки поверхности полярным углом θ, отсчитываемым от направления, противоположного Е, и азимутальным углом α. Легко видеть, что σ' = Р_n = = Р cos θ Из соображе­ний симметрии ясно, что создаваемое связанными зарядами поле имеет такое же направление, как и поле в диэлектрике Е. Поэтому для его вычисления нужно от каждого вектора напряженности dЕ_доп, создаваемого связанным зарядом элемента поверхности dS, взять составляющую dЕ в направлении Е и затем сложить эти составляющие для всех элементов поверхности.

Выразим элемент поверхности в сферической системе координат:

На нем помещается заряд

к оторый создает в центре сферы поле напряженности

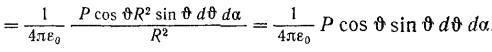
С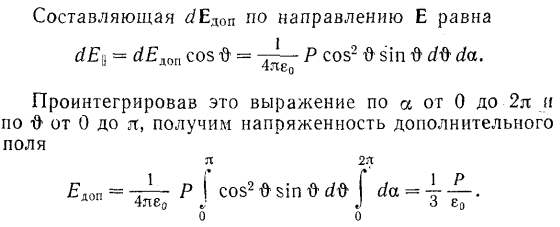 ледовательно, напряженность поля в центре сферической полости равна (**)

В гауссовой форме формула имеет вид

Каждая отдельно взятая молекула диэлектрика помещается как бы в центре сферической полости. Строгий расчет показывает, что поле, действующее на отдельно взятую молекулу, точно совпадает с (**) только в случае кристаллического диэлектрика кубической системы. Для жидких и газообразных диэлектриков напряженность поля, действующего на отдельную молекулу, определяется значением (**) лишь приближенно.