Уравнение Бернулли

Уравнение вида

(1)

называется уравнением Бернулли.

Прежде всего отметим, что при 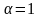уравнение (1) принимает вид

то есть является уравнением с разделяющимися переменными, общее решение которого

Разумеется, считаем, что и непрерывны на некотором интервале .

Область изменения величины в (1) определяется значением , то есть областью существования функции .

Для решения д.у. (1) делаем замену

, (2)

то есть вместо одной неизвестной функции вводим две! Но появляется возможность при этом выбрать одну функций или , как будет удобнее. Постановка (2) в (1) дает

. (3)

Найдем из уравнения

(4)

то есть положим

. (5)

При этом среди первообразных для выберем наиболее удобную. С учетом (4) уравнение (3) принимает вид

Это уравнение с разделяющимися переменными и общее решение

(6)

его с учетом (5) имеет вид

(7)

По (2) окончательно

Разумеется, не следует запоминать формулу (7). Надо использовать алгоритм, описанный в (2) – (5).

Пример 1. Иллюстрируем сказанное примером:

Очевидно, что это д.у. имеет вид (1), если положить

Решать данное уравнение Бернулли можно лишь при условии

Замена приводит его к виду (3)

Если положить, как в (4)

то есть считать каким-то ненулевым решением уравнения с разделяющимися переменными, например (любое решение последнего д.у. очевидно есть 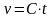), то для получаем дифференциальное уравнение

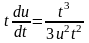
или

откуда

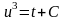и

Окончательно

Как было отмечено, что влечет ограничение

Пример 2. Решим следующее уравнение Бернулли, требующее дополнительных исследований:

(8)

Это уравнение Бернулли с Очевидно, что , и - решение данного уравнения. Отметим, что - решение любого уравнения Бернулли с . Таким образом, достаточно рассматривать решения (8) в первом и во втором квадратах. Так как (8) можно записать в виде

(9)

и функции

непрерывные в указанных квадрантах, то в них имеет место существование и единственность решения задачи Коши для д.у. (8), (9). Так как правая часть (9) нечетная по функция, то если а , очевидно, глобальная картина интегральных линий симметрична относительно оси (вертикальной). Поэтому достаточно решать уравнение (8) или (9) в первом квадранте .

Произведя в (8) замену (2), получаем

. (10)

Положим [как в (4)] . Для (так как 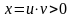) это уравнение равносильно

- уравнение с разделенными переменными, откуда .

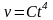Проще всего считать и выбрать . Тогда для получаем из (10) уравнение

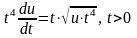
или

. (11)

Здесь следует сделать важное замечание: . Уравнение (11) – с разделяющимися переменными и

.

В силу сделанного замечания и

. (12)

Для . Имеем

и

. (13)

Решение является особым.

Если не отмечать в (13) условие , то функция оказывается определенной на всей прямой .

Очевидно, что нарушена единственность решения задачи Коши в первом и втором квадрантах. Следует из того, что по (9) при производная и возрастает на интервале определения для положительных значений .

Уравнения в полных дифференциалах

Рассмотрим дифференциальное уравнение

. (11.1)

Предположим, что , дифференцируемые в некоторой области .

Определение. Если левая часть уравнения (11.1) представляет собой полный дифференциал некоторой функции , то (11.1) называется уравнением в полных дифференциалах.