
- •2.2.2. Тема: Дифференциальные уравнения первого порядка (5-часов)
- •Дифференциальные уравнения первого порядка
- •Рассмотрим дифференциальное уравнение вида
- •Общий интеграл его есть
- •Линейные уравнения первого порядка.
- •Уравнение Бернулли
- •Другими словами, уравнение (11.1) представляется в виде
- •7. Линейные дифференциальные уравнения первого порядка. Метод подстановки Бернулли.
- •2.2.3 Тема: Дифференциальные уравнения высших порядков (3-часа) Линейные дифференциальные уравнения -го порядка
- •Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •Метод Лагранжа (метод вариации произвольных постоянных)
- •2.2.4 Тема: Системы линейных дифференциальных уравнений с постоянными коэффициентами (3-часа)
- •Системы обыкновенных дифференциальных уравнений
- •Метод Эйлера
2.2.2. Тема: Дифференциальные уравнения первого порядка (5-часов)
Основные понятия
Определение.
Дифференциальным уравнением называется
уравнение, связывающее независимую
переменную
 ,
искомую функцию
,
искомую функцию
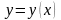 и ее производные
и ее производные
 т.е. уравнения вида
т.е. уравнения вида
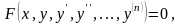 (2,1)
(2,1)
где
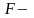 непрерывная функция
непрерывная функция
 переменных.
переменных.
Если искомая функция есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным.
Например,

Если искомая функция зависит от нескольких независимых переменных, то дифференциальное уравнение называется уравнением в частных производных.
Например,

В дальнейшем будем рассматривать лишь обыкновенные дифференциальные уравнения.
Порядком дифференциального уравнения называется порядок наивысшей производной, явно входящей в уравнение.
Например:
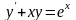 -
дифференциальное уравнение 1- го порядка;
-
дифференциальное уравнение 1- го порядка;
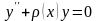 -
дифференциальное уравнение 2- го порядка;
-
дифференциальное уравнение 2- го порядка;
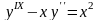 - уравнение 9- го
порядка.
- уравнение 9- го
порядка.
Решением
дифференциального
уравнения (2.1) называется функция
 которая при подстановке в дифференциальное
уравнение обращает его в тождество.
которая при подстановке в дифференциальное
уравнение обращает его в тождество.
Например,
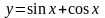 является решением дифференциального
уравнения
является решением дифференциального
уравнения
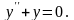
В самом деле,
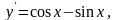
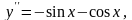

Процесс отыскания решений дифференциального уравнения называется интегрированием уравнения.
График решения дифференциального уравнения называется интегральной кривой этого уравнения.
Дифференциальные уравнения первого порядка
Общий вид уравнения первого порядка следующий:
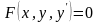 (3.1).
(3.1).
Если уравнение
(3.1) удается разрешить относительно
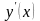 ,
то получим
,
то получим
 (3.2).
(3.2).
Это уравнение называется уравнением первого порядка, разрешенным относительно производной.
Задача Коши. Теорема существования и единственности
Для уравнения 1- го порядка справедлива следующая теорема:
Теорема (о существовании и единственности решения дифференциального уравнения первого порядка).
Если в уравнении
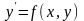 функция
функция
 и ее частная производная
и ее частная производная
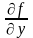 непрерывны в некоторой области
непрерывны в некоторой области
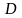 на плоскости
на плоскости
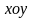 ,
содержащей точку
,
содержащей точку
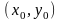 ,
то в некоторой окрестности точки
,
то в некоторой окрестности точки
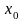 существует единственное решение этого
уравнения
существует единственное решение этого
уравнения
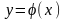 ,
удовлетворяющее условию: при
,
удовлетворяющее условию: при
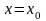 ,
,
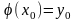 .
.
Геометрический смысл теоремы заключается в том, что существует и притом единственная функция , график которой проходит через точку .
Условие, что при
функция
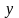 должна равняться заданному числу
должна равняться заданному числу
 ,
называется
начальным
условием.
Оно записывается в виде
,
называется
начальным
условием.
Оно записывается в виде
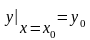 .
.
Задача отыскания решений уравнения, удовлетворяющего начальным условиям, носит название задачи Коши.
Из сформулированной теоремы следует, что уравнение (3.2) имеет бесконечное число различных решений, ибо через каждую точку области проходит одно решение.
Уравнения с разделяющимися переменными
Рассмотрим дифференциальное уравнение вида
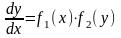 (6.1)
(6.1)
где правая часть есть произведение функции, зависящей только от , на функцию, зависящую только от .
Предполагая, что
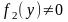 ,
преобразуем его следующим образом:
,
преобразуем его следующим образом:
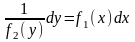 .
(6.
.
(6.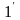 )
)
Считая известной функцией от , равенство (6. ) можно рассматривать как равенство двух дифференциалов, а неопределенные интегралы от них будут отличаться постоянным слагаемым.
Интегрируя левую часть по , а правую по , получим
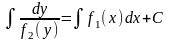 .
.
Мы получили
соотношение, связывающее решение
,
независимое переменное
и произвольную постоянную
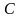 ,
т.е. получили общий интеграл уравнения
(6.1).
,
т.е. получили общий интеграл уравнения
(6.1).
Дифференциальное уравнение типа (6. ) или вида
 (6.2)
(6.2)
называют уравнением с разделенными переменными.
