Ряд Маклорена имеет вид

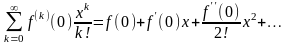(30)

а остаточный член Тейлора в форме Лагранжа

(31)

где 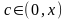или .

Разложение в ряд Маклорена основных элементарных функций

1. Показательная функция .

Поскольку для любого  то . Подставив эти значения в (10.30), получим ряд Маклорена для этой функции. Проверим условия теоремы 2.

Для любого фиксированного из (31) получим

. (32)

Согласно признака Даламбера ряд сходится для всех . Поэтому согласно необходимого признака и из (32) получаем что .

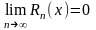Окончательно имеем разложение функции в ряд Маклорена для

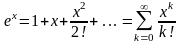. (33)

Пример 23. Вычислим число с точностью до  для чего воспользуемся рядом (33) при получим .

Оценим остаточный член 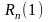с помощью (32) получим что

.

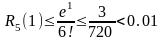Поэтому с требуемой точностью

.

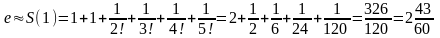2. Функция .

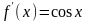
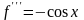
Поскольку 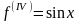    и т.д., то

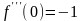
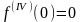    и т.д.

Из (30) получим что

. (34)

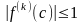
Поскольку  то для любого

и, как было показано выше для всех . Поэтому разложение (34) справедливо для .

Пример 24. Вычислим с точностью до 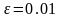. Для нахождения интеграла воспользуемся разложением в степенной ряд подинтегральной функции и свойством 2) об интегрировании равномерно сходящихся степенных рядов. Из (34) получаем что 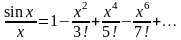и этот ряд равномерно сходится на любом отрезке поэтому

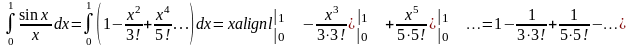
В результате получился знакочередующийся ряд, удовлетворяющий признаку Лейбница. Поскольку, согласно следствию из признака Лейбница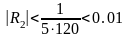 то с требуемой точностью 

3) Функция .

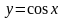Разложение в ряд Маклорена этой функции проведите самостоятельно по аналогии с предыдущим.

Для любого

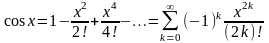
3. Степенная функция .

Вычислим значения .

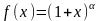
      и т.д.

С помощью индукции доказывается что

.

Подставив эти значения в (10.30) , получим что

.

Можно доказать что этот ряд сходится и равенство выполняется для любых действительных и .

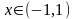Данный ряд называется биномиальным поскольку для целых положительных коэффициенты ряда совпадают с коэффициентами бинома Ньютона.

Пример 25. Вычислим с точностью до число .

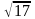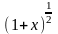
Заметим что нельзя применять последнее разложение для функции  при  поэтому поступим следующим образом

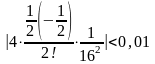
Получился знакочередующийся ряд, удовлетворяющий условиям признака Лейбница (проверьте!). Поскольку  то с требуемой точностью .

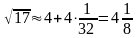4. Логарифмическая функция 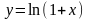.Воспользуемся формулой суммы геометрической прогрессии для :

Поскольку ряд равномерно сходится на промежутке (или ) при  то проинтегрировав его по этому промежутку, получим

;

.

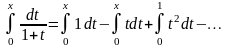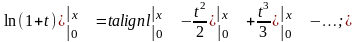
На самом деле данное разложение справедливо для .

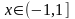6)

Интегрируя геометрическую прогрессию и ее сумму

по промежутку , получим что

.

Данное разложение верно для .

7) 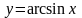. Запишем биномиальный ряд для 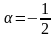и .

.

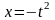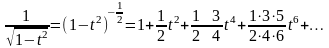Проинтегрировав ряд по промежутку , получим требуемое разложение

.

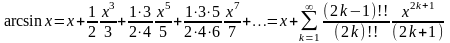Здесь ; ;

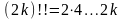Данное разложение справедливо для .

Основная литература

1. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.2 М.:Наука,1985г. (стр. 282-285)

2. Гусак А.А. Высшая математика Т.2. Мн.: Тетро Системс, 2001г. (стр. 151-160)

Контрольные вопросы:

1. Определение ряда Тейлора.

2. Разложение элементарных функций в ряд Тейлора.

3. Применение ряда Тейлора.