2.2.12. Тема: Ряды Тейлора (2-часа)

Выше было показано что сумма степенного ряда является бесконечно дифференцируемой функцией. Рассмотрим теперь обратную задачу о том, как заданную функцию записать в виде суммы некоторого степенного ряда. Такая запись позволит приближенно находить значения этой функции приближенно интегрировать ее численно решать дифференциальные уравнения и т.д.

Пусть функция имеет производные до го порядка включительно в окрестности точки .

Определение. Многочленом Тейлора го порядка функции в точке называется многочлен

Здесь 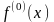считается равным 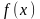и .

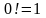Основное свойство этого многочлена состоит в следующем.

Значения многочлена и всех его производных до го порядка включительно в точке совпадают с соответствующими значениями функции и ее производных т.е.

; ; … … … ; .

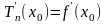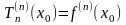При .

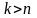
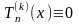В самом деле из (22), подставив вместо значение , получим

;

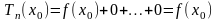Подставив сюда , получим

и т.д.

.

При .

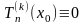Определение. Разность между и называется остаточным членом Тейлора с центром в :

Обозначим его через

Из (22) следует что

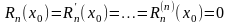(23)

Теорема 1. Пусть функция имеет в окрестности непрерывную 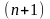ую производную .

Тогда для любого из этой окрестности найдется такая точка 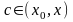или , что

(24)

При доказательстве воспользуемся теоремой Коши четвертого модуля «Дифференциальное исчисление функций одной переменной». Пусть 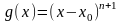. Несложно проверить что

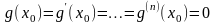(25)

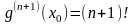. (26)

Пусть для определенности 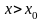. Рассмотрим отношение .

Здесь в числителе и знаменателе добавлены нулевые величины и .

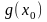Согласно теореме Коши найдется точка такая что

,т.е. учитывая (23) и (25) .

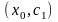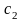Согласно теореме Коши в промежутке найдется точка такая, что

 .

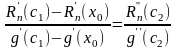
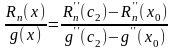Продолжая этот процесс раз получим что

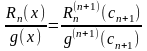(27).

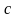
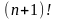
Обозначим через  заменим согласно (26) на  а .

В результате из (27) получаем ,что и доказывает требуемое утверждение.

Определение. Остаточный член 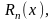записанный в виде (24) называется остаточным членом в форме Лагранжа а запись функции в виде

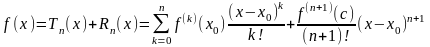(28)

называется формулой Тейлора с остаточным членом в форме Лагранжа.

Остаточный член здесь имеет тот же самый вид что и слагаемые многочлена Тейлора только в ой производной вместо стоит близкая к ней точка .

Многочлен Тейлора используется для приближенного нахождения значения функции в точке  при этом является погрешностью этого вычисления. Однако часто вместо многочленов удобно использовать ряды.

Определение. Пусть функция бесконечно дифференцируема в окрестности точки . Рядом Тейлора для функции с центром в точке называется смещенный степенной ряд

(29)

Частичная сумма этого ряда является многочленом Тейлора . (здесь и далее состоит из слагаемых). Не следует думать что сумма ряда Тейлора всегда совпадает с функцией  по которой он был построен, во-первых потому, что область определения функции может не совпадать с областью сходимости ряда а вовторых даже в случае существования и , эти значения могут отличаться друг от друга.

Теорема 2. Пусть функция бесконечно дифференцируема в окрестности 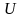точки  и пусть для всех из этой окрестности остаточный член Тейлора стремится к нулю при , тогда ряд Тейлора функции с центром в сходится в , и его сумма совпадает в со значениями функции .

В этом случае говорят что функция разлагается в ряд Тейлора в окрестности .

Учитывая что 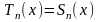запишем формулу Тейлора (28) для

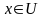
 или .

Перейдем в этом соотношении к пределу при получим .

Поскольку предел левой части существует и равен   то существует предел частичных сумм ряда (29), стоящий в правой части т.е. 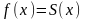что и требовалось доказать.

Определение. Ряд Тейлора с центром в точке называется рядом Маклорена этой функций.