2.2.11. Тема: Степенные ряды. (1-часа)

Степенные ряды т.е. ряды, члены которых есть степенные функции, являются одним из основных примеров функциональных рядов.

Определение. Функциональный ряд вида

(17)

называется степенным рядом а числа называются его коэффициентами.

Степенной ряд всегда сходится при . Следующая теорема описывает его область сходимости.

Теорема 1. (Теорема Абеля)

а) Если степенной ряд (17) сходится в точке ( ) то он сходится для всех из интервала 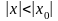(см. рис. 3,а)).

б) Если степенной ряд расходится в точке , то он расходится для всех , удовлетворяющих неравенству (см. рис.3,б)).

Рис. 3, а).

Рис. 3, б).

а) Так как ряд 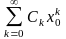сходится то согласно необходимому признаку  откуда следует, что последовательность ограничена, т.е. существует число , такое что . Пусть . Рассмотрим абсолютную сходимость ряда . Получим

. (18)

Обозначим через , где и . Сравнивая с помощью первого признака сравнения ряд (18) и сходящуюся геометрическую прогрессию , получаем что (18) сходится. Допустим что найдется такое, что для которого ряд (10.17) сходится. Тогда согласно пункту а) поскольку он должен сходится в точке . Противоречие.

Определение. Наибольшее значение такое, что в интервале степенной ряд (10.17) сходится, называется радиусом сходимости этого ряда (обозначается через 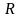) а интервал называется его интервалом сходимости.

Из теоремы Абеля следует что в интервале ряд (10.17) сходится а в интервалах и он расходится (см. рис. 4).

сходится

расходится расходится

Рис. 4.

Сходимость ряда в точке исследуется дополнительно.

Если ряд сходится только в точке  то считается равным  а если он сходится для всех , то считается равным .

Для определения радиуса сходимости имеются следующие формулы получаемые из признаков Даламбера и Коши.

 (19)

(20)

Однако проще находить интервал сходимости путем непосредственного применения признаков Даламбера или Коши к абсолютным величинам членов ряда (17).

Пример22. Найдем область сходимости ряда .

Исследуем абсолютную сходимость этого ряда с помощью признака Даламбера получим .Отсюда получаем что при , т.е. в интервале (11) этот ряд сходится а при , т.е. в интервалах и он расходится. Поэтому радиус сходимости ряда и интервал сходимости есть (11).

Исследуем концы этого интервала. Подставив в ряд, получим числовой ряд , который является гармонический расходящимся рядом. Подставив , получим знакочередующийся ряд .Выше с помощью признака Лейбница было проверено что он сходится. Окончательно получаем, что область сходимости исследуемого ряда есть Теорема 2. Пусть отрезок лежит в интервале сходимости 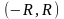степенного ряда ,тогда в этот ряд сходится абсолютно и равномерно.

Пусть для определенности . Для этот ряд сходится. Далее повторяем доказательства а) теоремы Абеля для . Перенесем теперь рассмотренные выше свойства равномерно сходящихся рядов на случай степенных рядов.

Свойства степенных рядов.

Сумма степенного ряда (17) непрерывна в интервале сходимости .

Это следует из того что любое можно заключить в отрезок , в котором ряд (17) сходится равномерно.

1. Пусть сумма степенного ряда (17) и отрезок лежит в интервале сходимости , тогда .

Здесь в правой части равенства стоит сумма интегралов членов ряда (17) .

3) Производная суммы степенного ряда (17) в интервале сходимости равна сумме степенного ряда, составленного из производных членов ряда (17), т.е. .

Здесь мы оставили без доказательства тот факт что ряд из производных ряда (17) имеет тот же интервал сходимости .

4) Сумма степенного ряда (17) в интервале бесконечно дифференцируема.

Это следует из того что согласно свойству 3) является суммой степенного ряда поэтому операцию дифференцирования можно провести еще один раз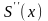 снова является суммой степенного ряда в и т.д.

Определение. Функциональный ряд

(21)

называется смещенным степенным рядом с центром в .

Если обозначить через , то смещенный степенной ряд превращается в степенной ряд вида (10.17). Поэтому ряд (10.21) имеет интервал сходимости вида и в этом интервале обладает всеми свойствами степенных рядов.

Основная литература: [1], стр. 406-416

Дополнительная литература: : [15]часть II стр. 131-139

Контрольные вопросы:

1. Определение степенных рядов.

2. Радиус сходимости степенного ряда.

3. Область сходимости степенного ряда.