Пример14. Выше было проверено что ряд

(13)

сходится согласно принципу Лейбница. Ряд из абсолютных величин его членов есть расходящийся гармонический ряд .

Поэтому ряд (13) сходится условно.

Теорема 8. Если ряд (10) сходится абсолютно то он сходится.

Доказательство. Пусть частичная сумма ряда (10) сумма положительных слагаемых из  а сумма модулей отрицательных слагаемых из . Тогда

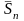
Пусть  частичная сумма ряда из абсолютных величин (12) и 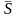его сумма тогда 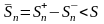.Поскольку положительные последовательности и возрастают, и ограничены сверху то имеются пределы 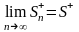и 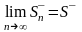, следовательно, существует предел , что означает что ряд (10) сходится.

Если все члены ряда положительны или ряд имеет только конечное число отрицательных членов, то сходимость такого ряда может быть только абсолютной. Условие «исследовать сходимость ряда» для ряда общего вида означает установление факта сходимости этого ряда и  в случае сходимости проверку того, как сходится этот ряд  абсолютно или условно.

Необходимость этого объясняется существенно различными свойствами абсолютно и условно сходящихся рядов.

Теорема 9. При любой перестановке членов абсолютно сходящегося ряда эта сходимость не нарушается и сумма ряда не изменяется.

Казалось что свойство «от перемены мест слагаемых сумма не меняется» должно выполняться всегда. Однако, для бесконечных сумм это не всегда так.

Пример 15. Рассмотрим условно сходящийся ряд

.

Согласно признака Лейбница его сумма

Переставим слагаемые в этом ряду следующим образом

Подсчитав значения стоящие в скобках, получим ряд

,

члены которого в два раза меньше членов исходного ряда. Значит, после указанной перестановки сумма ряда изменилась и стала равна .

Теорема 10. Если числовой ряд сходится условно то для любого числа А можно так переставить члены этого ряда что сумма полученного ряда станет равной А, кроме того можно так переставить члены условно сходящегося ряда что он станет расходиться.

Основная литература:

1. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.2 М.:Наука,1985г. (стр. 263-266)

2. Гусак А.А. Высшая математика Т.2. Мн.: Тетро Системс, 2001г. (стр. 127-135)

Контрольные вопросы:

1. Определение знакопеременного ряда.

2. Знакочередующиеся ряды. Теорема Лейбница.

3. Абсолютная и условная сходимости.

4. Признак абсолютной сходимости.

2.2.10. Тема: Функциональные ряды. (1-час)

Рассмотрим теперь ряды, членами которого являются не числа, а функции.

Определение. Функциональным рядом называется выражение вида

, (14)

где есть некоторые функции действительного переменного, имеющие общую область определения.

При подстановке вместо конкретных значений функциональный ряд (14) превращается в числовой ряд.

Определение. Областью сходимости функционального ряда (14) называется множество всех значений , при которых ряд (14) сходится.

Эту область будем обозначать через .

Пример16. Для каждого значения функциональный ряд

является рядом Дирихле.

Поэтому этот ряд сходится только при , т.е. его область сходимости есть интервал .

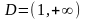Пример17. Ряд

является геометрической прогрессией со знаменателем .

Поэтому его областью сходимости является интервал .

Для функционального ряда (10.14) его частичная сумма  сумма и остаток 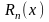есть функции, определенные в области .

В последнем примере в интервале (11) ;

;

.

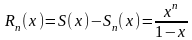Пусть некоторый промежуток, принадлежащий .

Определение. Функциональный ряд (10.14) называется равномерно сходящимся в , если наибольшее значение модуля его остатка в стремится к нулю при , т.е. .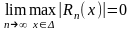

Заметим что хотя остаток в всегда стремится к нулю, но равномерно в он может к нулю не стремится.

Пример18. Рассмотрим ряд в промежутке .

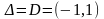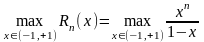не существует поскольку .

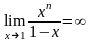Следовательно, в ряд сходится неравномерно.

Если рассмотреть  то  т.к. при числитель дроби принимает свое наибольшее значение, а знаменатель наименьшее. Поэтому и в промежутке этот ряд сходится.

В этом промежутке исследуемый ряд сходится равномерно.

Проверка равномерной сходимости ряда исходя из определения часто есть трудоемкая работа поэтому практически используют признаки равномерной сходимости функциональных рядов.

Определение. Числовой ряд

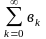(2)

называется мажорирующим для функционального ряда

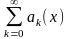(14)

на промежутке , если для всех и любого верно неравенство

. (15)

Если промежуток не указывается то это неравенство должно выполнятся для всех действительных .

Теорема 1. ( Признак равномерной сходимости Вейерштрасса).

Пусть для ряда (14) в промежутке имеется сходящийся мажорирующий ряд (2). Тогда (14) равномерно сходится в .

Из неравенства (15) и первого признака сравнения следует что (14) сходится в .

Пусть остаток ряда (14) а 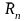остаток ряда (2), тогда из неравенства (15) получим .

Следовательно, .

Перейдя в обеих частях этого неравенства к пределу при , получим ,что

для всех т.е. .

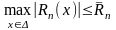Поскольку ряд (10.2) сходится то 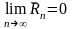, следовательно .

Пример 19. Проверим, что ряд 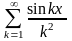равномерно сходится на всей числовой оси.

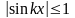
Поскольку  то . Поэтому ряд мажорирует данный ряд для . Поскольку числовой ряд Дирихле сходится  то функциональный ряд сходится равномерно на .

Необходимость выделять равномерную сходимость связана с тем, что равномерно сходящиеся ряды обладают рядом естественных свойств, которых лишены неравномерно сходящиеся ряды.

Свойства равномерно сходящихся рядов.

1. Пусть ряд равномерно сходится в промежутке и все его члены непрерывны в , тогда сумма этого ряда также непрерывна в .

Доказательство. Пусть 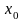внутренняя точка в . Из того, что 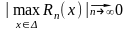и непрерывны в следует что для каждого найдется такой номер , что выполняется неравенство 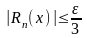для всех . Кроме того, найдется число 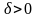, такое что для всех выполняется неравенство .

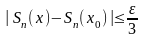Используя эти два неравенства, получаем, что для всех верно

что означает верность равенства 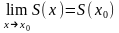и непрерывность в . Случай граничной точки рассмотрите сами.

В следующей лекции будет приведен пример неравномерно сходящегося ряда с непрерывными слагаемыми сумма которого разрывна.

2) Пусть ряд равномерно сходится в отрезке и имеет сумму . Пусть все члены ряда непрерывны в отрезке тогда интеграл по от суммы ряда равен сумме интегралов от его слагаемых т.е.

Из свойства 1) следует что и непрерывны на . Проинтегрировав соотношение , получим

. (16)

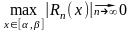
Поскольку и  то .Перейдя в равенстве (10.16) к пределу при , получим требуемое утверждение.

Пример 20. Выше было проверено, что геометрическая прогрессия 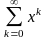равномерно сходится в промежутке и имеет сумму . Применив свойство 2) к отрезку , получим, что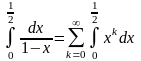 .Вычислим записанные интегралы .

Следовательно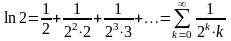 .Этот пример показывает, что с помощью почленного интегрирования можно находить суммы числовых рядов.

3. Пусть члены сходящегося в ряда

непрерывно дифференцируемы в промежутке и -сумма этого ряда. Пусть ряд, составленный из производных ряда 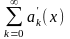,равномерно сходится в , тогда сумма ряда из производных равна производной , т.е. .

Обозначим сумму ряда через 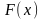. Согласно предыдущему свойству проинтегрируем на отрезк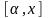е , где 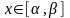, получим .Продифференцируем по левую и правую части этого равенства получим  .

Пример21. Рассмотрим сходящуюся геометрическую прогрессию

на промежутке . Сумма этого ряда .Ряд из производных записывается в виде и мажорируется сходящимся рядом 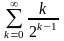. (Проверьте сходимость этого ряда с помощью признака Даламбера). Поэтому ряд из производных равномерно сходится в отрезке . Согласно свойству 3) получим .С помощью дифференцирования также можно находить суммы числовых рядов. Например подставив в последнее соотношение  получим .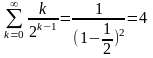

Основная литература:

1. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.2 М.:Наука,1985г. (стр. 266-275)

2. Гусак А.А. Высшая математика Т.2. Мн.: Тетро Системс, 2001г. (стр. 135-146)

Контрольные вопросы:

1. Определение функционального ряда.

2. Область сходимости.

3. Равномерная сходимость функциональных рядов.