Поверхность отклика второго порядка

Пусть поверхность отклика есть поверхность второго порядка, а область действия факторного пространства – единичный гиперкуб.

Общий вид:

где /

Измерение величины y в разных точках x_i предполагается равноточные, т.е. .

Набор функций в данном случае будет такой:

Размерность вектора равна .

Пример: k = 2

Тогда поверхность отклика будет иметь вид:

Для рассматриваемого случая непрерывный D – оптимальный план имеет следующий вид:

Измерения с одинаковыми весами  производятся в каждой из 2^к вершинах к – мерного куба; с одинаковыми весами  в каждой из к2^к-1 точек, являющихся серединами рёбер куба; и с одинаковыми весами  в каждой из к(к - 1)2^к-3 центров двумерных граней.

Т.о. спектр суммарного плана содержит:

различных точек.

При к = 2, n = 9, (m = 6) => план ненасыщенный.

Приведём значения для некоторых к:

к			
2	0,1458	0,08015	0,0962
3	0,071975	0,01895	0,03280
4	0,03705	0,0038375	0,01185
5	0,01928	0,0003125	0,04485

Если например:

к = 3 и N = 100, то в каждой из 2^к = 2³ = 8 вершин куба производится  72 измерения, в каждой из к2^к-1 = 32^3-1 = 12 середин рёбер куба производится  19 измерения, в каждом из к(к - 1)2^к-3 = 322^3-3=6 центров двумерных граней производится  33 измерения.

Всего 872 + 1219 + 633  1000 измерений.

Координаты вершин к – мерного куба принимают значения “1” или “-1”.

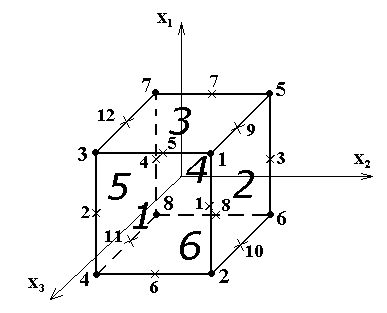
Координаты вершин куба:

1	2	3	4	5	6	7	8
(1,1,1)	(1,1,-1)	(1,-1,1)	(1,-1,-1)	(-1,1,1)	(-1,1,-1)	(-1,-1,1)	(-1,-1,-1)

Координаты середин рёбер куба:

1	2	3	4	5	6
(1,1,0)	(1,-1,0)	(-1,1,0)	(-1,-1,0)	(1,0,1)	(1,0,-1)
7	8	9	10	11	12
(-1,0,1)	(-1,0,-1)	(0,1,1)	(0,1,-1)	(0,1,-1)	(0,-1,1)

Координаты центров двумерных граней куба:

1	2	3	4	5	6
(1,0,0)	(0,1,0)	(0,0,1)	(-1,0,0)	(0,-1,0)	(0,0,-1)