Насыщенный d – оптимальный план.
Описанный выше оптимальный план при большом m требует измерения y в 2m точках факторного пространства. Для рассматриваемого случая линейной регрессии на кубе можно доказать существование D – оптимального плана, который содержит всего m+1 точку.
Координаты i – той точки этого плана – есть элементы строки матрицы Адамара порядка (m+1)(m+1). Матрица Адамара ‑ А определяется следующими условиями:
1) Любой элемент aij может принимать значение либо «+1», либо «-1».
2)
,
где
‑ единичная матрица порядка n.
Матрица Адамара существует лишь для n,
кратных четырём, т.е. n=4k,
где k
– целое положительное число. В настоящее
время матрица Адамара построена для
всех
,
кроме k=47.
Если число m+1
определяемых параметров не удовлетворяет,
условию m+1=4k
то D
– оптимальный план в этом случае может
быть получен из D
– оптимального плана для ближайшей
большей по размерности матрицы Адамара
(m1+1)(m1+1)
вычеркиванием из неё любого одного (или
двух или трёх) столбцов, в зависимости
от величены разницы (m1+1)
‑ (m+1).
Например: при m+1=29 следует рассматривать матрицу Адамара размерности 32*32, и из неё следует вычеркнуть 32-29=3 столбца. Полученный план уже не будет насыщенным, т.к. число точек его спектра будет на 1, 2 или 3 превышать число определённых параметров. В качестве примера рассмотрим Матрицу Адамара дляn = 8, т.е. m = 7.
|
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
1 |
1 |
-1 |
-1 |
-1 |
1 |
-1 |
1 |
-1 |
2 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
1 |
1 |
3 |
1 |
-1 |
1 |
-1 |
-1 |
-1 |
-1 |
1 |
4 |
1 |
1 |
1 |
-1 |
1 |
-1 |
-1 |
-1 |
5 |
1 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
6 |
1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
-1 |
7 |
1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
8 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Линейная регрессия. D – оптимальный план на сфере
Рассматривается линейная регрессия такого вида:
Но область действия факторного пространства задаётся в виде m–мерной гиперсферы с центром в начале координат и с радиусом равным 1.
Уравнение гиперсферы:
М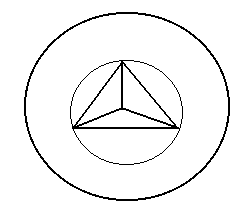
ожно
доказать, что существует множество
оптимальных насыщенных планов с числом
точек спектра равным m+1.
Каждый такой план реализуется в вершинах
правильного m–мерного
симплекса (т.е. многогранника), вписанного
в сферу. Число вершин m–мерного
симплекса равно m+1.
Двумерным симплексом является правильный треугольник.
Трёхмерным – правильный тетрайдер.
Один из возможных D ‑ оптимальных планов имеет вид:
|
x1 |
x2 |
x3 |
. . . |
xm |
1 |
c - r |
- r |
- r |
|
- r |
2 |
- r |
c - r |
|
|
- r |
3 |
- r |
- r |
c - r |
|
- r |
. . . |
|
|
|
|
|
m |
- r |
- r |
- r |
- r |
c - r |
m + 1 |
a - r |
a - r |
a - r |
a - r |
a - r |
Для m = 3 получим точки, в которых необходимо производить изменения для того, что бы план был оптимальный.
Точек будет m + 1
-
x1
x2
x3
1
2
3
4
Чем меньше область действия, тем меньше максимум дисперсии поверхности отклика, поэтому этот максимум на гиперсфере единичного радиуса меньше, чем на единичном кубе.
при m
= 3
.
Если количество измерений N = 100, то в каждой точке надо делать 25 измерений.