17

Часть V. Построение оптимальных планов экспериментов. Показатели качества эксперимента. Функция потерь.

Планирование эксперимента заключается в выборе числа измерений N, точек факторного пространства Х, в которых производится измерение y, чисел r_i, измерений y в точке , обеспечивающих желаемую точность определения y, в определении затрат (материальных, денежных, трудовых и т.д.) на проведение этих мероприятий.

В теории планирования эксперимента показателем качества проведения эксперимента является функция и потерь R().

Оптимальным называется план эксперимента *, минимизирующий R().

Достаточно широкое распространение получило представление R() в виде:

R() = () + () , (1)

где () – учитывает затраты на проведение эксперимента.

, (2)

где с_i – стоимость одного измерения в точке ;

r_i – количество измерений в точке ;

() – характеризует точность проведения эксперимента.

Большую часть всей практически допустимой информации о точности проведения эксперимента содержит дисперсионная (ковариационная) матрица D{}, каждый элемент которой

(3)

В случае линейной по параметрам поверхности отклика

Обозначение D{} говорит о том, что матрица относится к данному эксперименту.

‑ информационная матрица Фишера.

Включить всю информацию, содержащуюся в D{}, в член () непросто, т.к. это сильно бы затруднило процесс минимизации R(). При определении оптимального плана эксперимента обычно идут на компромисс:

4а) – Минимизирует объём эллипсоида в m-мерном пространстве параметров. В центре эллипсоида лежат истинные значения искомых параметров. Чем меньше объём эллипсоида, тем ближе оценки прилегают к истинному значению.

4б) – В () входит сумма элементов дисперсионной матриц, расположенных на диагонали. Эта сумма минимизируется.

4в) – В () входит максимальный элемент диагонали дисперсионной матрицы. Добиваются его минимизируют.

4г) – Определяется максимальное значение дисперсии поверхности отклика и его минимизация.

Число k – нормирующий множитель, обеспечивающий одинаковую размерность двух слагаемых функции потерь R() и задающий вес слагаемого () в R(). Такое большое количество представлений {} объясняется тем, что нет его универсального единственного представления, которое позволило бы и математически решать поставленную задачу и обеспечивать заданную точность проведения эксперимента. Некоторые варианты хуже с метрологической точки зрения. Например 4а) оказывается более удобной с вычислительной точки зрения, что облегчает определение оптимального плана эксперимента ОПЭ.

Проблемы, связанные с построением ОПЭ.

Любой план определяется числом измерений N, точками факторного пространства, в которых производится измерение и величинами количества измерений r₁, r₂, r_n.

Процедуру выбора ОПЭ удобно производить для нормированного плана, в котором вместо величин r_i задаются относительные величины измерения.

Пусть для плана эксперимента  функция потерь

(5)

При переходе к нормированному плану

, где (6)

Матрица получается из заменой r_i на р_i .

‑ диагональные элементы матрицы .

Дисперсия поверхности отклика определяется из выражения заменой

После построения функции потерь задача ОПЭ сведена к определению минимума функции потерь R по аргументам N и спектру плана ( ). В этой задаче объём необходимых вычислений очень быстро растёт с ростом размерности факторного пространства m. Однако при некоторых дополнительных предположениях решение задачи существенно упрощается.

1) Общее число измерений N фиксировано.

Если стоимость измерений величины y не зависит от расположения точки x_i, т.е. если С_i = C = const, то функция потерь принимает вид:

.

Тогда

,

т.е. надо исткать , по всем точкам факторного пространства:

Эта задача существенно проще чем поиск по N и .

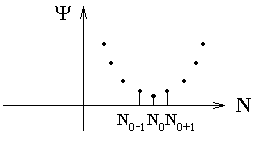
2) Фиксирована точность определения оценок.

Задаётся требование:

Планирование эксперимента в этом случае состоит в том, что фиксируют N и находят: .

Затем N увеличивают до тех пор, пока не будет найдены N_о и , при которых

3) Непрерывные планы.

В непрерывных планах число N очень велико. Непрерывный план определяется соотношениями:

Если использовать непрерывный нормированный план, то p_i будет любое число.

Непрерывный нормированный план не зависит от общего числа измерений N, т.е. от N не зависит и поэтому при минимизации функции потерь можно сначала провести минимизацию по N т.е. , (т.к. есть член ), и найдя из этого условия N, которое для варианта (4а) будет равно:

m – количество различных факторов.

Для вариантов (4 б, в, г):

Функция потерь при любом фиксированном N является возрастающей функцией от дисперсионной матрицы или от , а следовательно минимальное значение R достигается при таком непрерывном плане который минимизирует или .

Оптимальный план называется насыщенным, если он реализуется на минимальном по сравнению с остальными оптимальными планами числе различных точек факторного пространства.