Вспоминая формулу для вектора мнк оценок

где матрица Z и вектор описаны выше.

Для рассматриваемого случая

Поэтому

, а вектор измеренных значений выходной величины y₂

имеет вид

Вектор определяется теперь по известной формуле и по нему находится расчетная переменная

Затем переходим ко второму уравнению и выписываем выражение для эндогенной переменной y₁ в его правой части

y₁ = q₁₁x₁ + q₁₂x₂ + ₁

и повторяем для него выкладки, аналогичные только что сделанным.

Находим расчётную переменную:

Для второго уравнения находим также и расчётную переменную

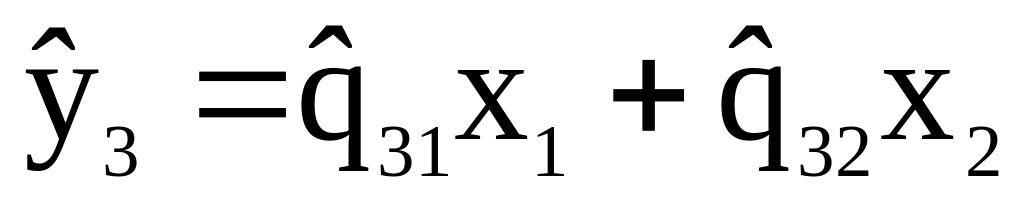
У третьего уравнения эндогенная переменная отсутствует и поэтому первый шаг окончен.

Второй шаг. Теперь вместо исходной системы рассматривается система

Для каждого из этих уравнений, независимо применяя МНК, находим наилучшие оценки коэффициентов .

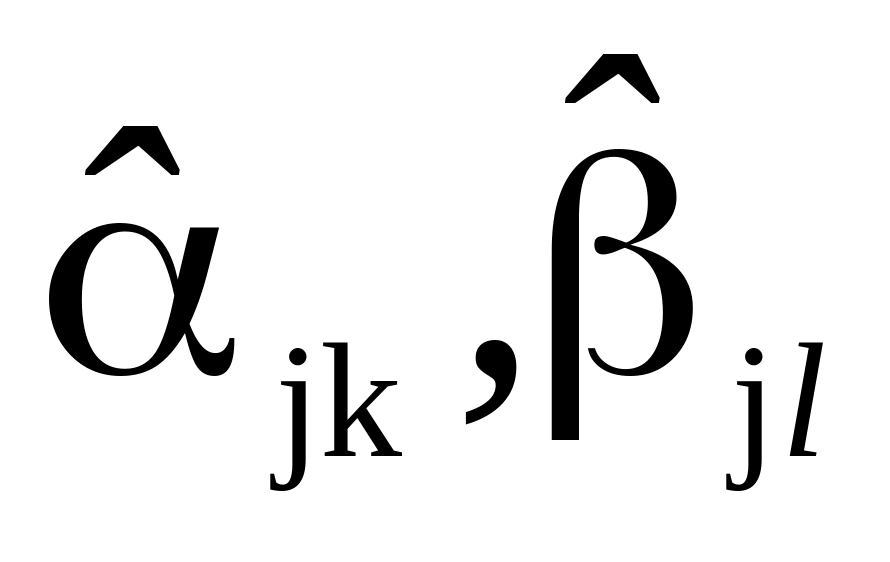При этом для первого уравнения факторами (контролируемыми переменными) считаются , для второго ‑ , для третьего – x₂.

Значения переменных х₁, х₂ при применении МНК на втором шаге выбираются из матрицы экспериментальных данных Х, а значения , соответствующие каждому из N наблюдений, рассчитываются по полученным выше формулам.