12

Часть III Развитие методов регрессионного анализа.

До сих пор математическая модель изучаемого явления рассматривалась как линейная регрессионная функция вида:

где y – скалярная выходная величина;

‑ точка факторного пространства, координатами которой являются входные величины (факторы, контролируемые переменные, x _i)

‑ вектор параметров (неизвестных)

‑ вектор базовых функций (заранее заданных)

‑ математическое ожидание случайной (из-за наличия помех при измерениях) величины y в заданной точке факторного пространства . Пусть в процессе проведения эксперимента выполнено N измерений выходной величины y в точках факторного пространства.

Описание эксперимента можно представить в виде линейной модели наблюдений:

где ‑ вектор измеренных значений выходной величины

‑ вектор ошибок измерений

‑ матрица линейной модели

Т.к. y – случайная величина, то точное значение найти не можем, поэтому должны использовать его оценку.

Для определения по результатам эксперимента вектора параметров применяется метод наименьших квадратов (МНК).

МНК – оценка минимизирует ‑ сумму взвешанных квадратичных отклонений:

‑ учитывает неравноточность измерений.

МНК – оценка неизвестного вектора определяется соотношением:

М₁ – информационная матрица Фишера – не зависит от результатов измерений, а зависит лишь от расположения , т.е. от плана эксперимента. Элементы М₁ .

‑ обратная матрица, такая, что , где I – единичная матрица, элементы которой

здесь A_ji – минор матрицы М₁,

‑ определитель матрицы М₁.

‑ рассматривается случай равноточных – с одинаковой дисперсией – измерений величины y в разных точках .

Обратим ещё раз внимание, что рассмотренный выше случай относится к случаю одной выходной величины.

Перейдём к некоторым обобщениям регрессионного подхода.

Векторная функция регрессии

Пусть выходной величиной изучаемого объекта (явления) является вектор нескольких измеряемых величин (верхнее и нижнее управление)

Математическая модель явления имеет вид:

, где ,

Таким образом имеется n неизвестных векторных параметров . Все выходные величины y_ij зависят от одного и того же вектора факторного пространства. В системе (1) каждое из уравнений можно рассматривать независимо от другого и применять к каждому из них МНК в описанной выше постановке.

Структурные уравнения линейной регрессии

Рассматривается функционирование сложной системы (например, предприятия), состоящей из некоторого числа взаимосвязанных подсистем. Каждая подсистема характеризуется одним выходным параметром (выходной переменной).

Имеется некоторое число параметров, являющихся внешними (экзогенными) по отношению ко всей системе. Соответственно выходы всех подсистем называются эндогенными. Входами данной подсистемы могут быть как выходы некоторых других подсистем, так и часть экзогенных входов. Таким образом, структура изучаемой системы предполагаемой системы известной.

Пример, такой структуры изображен на рис.1.

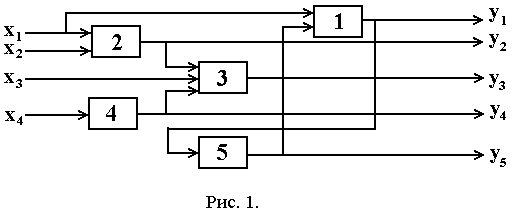
Пусть n – общее число подсистем, а, значит, и выходов подсистем y_n;

m – общее число экзогенных параметров (входов).

Обозначим через A_j – заранее известное подмножество индексов тех эндогенных параметров, которые являются входами j – той подсистемы;

Через B_j – подмножество индексов тех экзогенных параметров x_k, которые являются непосредственными входами j – той подсистемы.

Например для приведённой на Рис. 1. структуры:

n = 5, m = 4, A₃ = {2,4}, В₃ = {3}, A₂ = { }, В₂ = {1,2} и т.д.

Ограничимся случаем, когда каждая из подсистем описывается линейной моделью, т.е. выход каждой подсистемы является линейной функцией от её входов.

Тогда уравнения реальной системы имеют вид:

(1)

Здесь ‑ вектор ошибок (помех), отражающих отклонение реальной системы от её математической модели. (аппроксимационный подход).

Вместе с тем, вектор может рассматриваться и как вектор измеренных значений выходов подсистем, а вектор ‑ как вектор ошибок измерений.

Обозначим через А – матрицу коэффициентов в правой части системы (1) (А  М_nn), через В – матрицу коэффициентов правой части системы (1) (В  М_nm). Тогда систему (1) можно записать в векторно-матричной форме:

(2)

Единственное ограничение, накладываемое на систему уравнений (1) или (2) состоит в требовании, чтобы она была разрешима относительно эндогенных переменных y_i, т.е. должно выполнятся условие:

(3)

Здесь I – единичная матрица размерности nn ;

‑ определитель матрицы .

Система (1) или векторно-матричное уравнение (2) называются структурными уравнениями регрессии. В этих уравнениях являются неизвестными и подлежащими определению коэффициенты и или соответственно матрицы А и В.

Следует особо отметить, что часть элементов и известны (и равны = 0), поскольку известна структура системы. Если например, сигнал x₃ не поступает на вход подсистемы с выходным сигналом y₅, то коэффициент = 0.

Если эндогенный параметр y₂ не поступает на вход подсистемы с выходом y_4, то .

Таким образом, заранее известны все нулевые элементы матриц А и В.

Предположим, что имеется N наблюдений за состояниями входов и выходов системы, т.е. имеются матрицы данных:

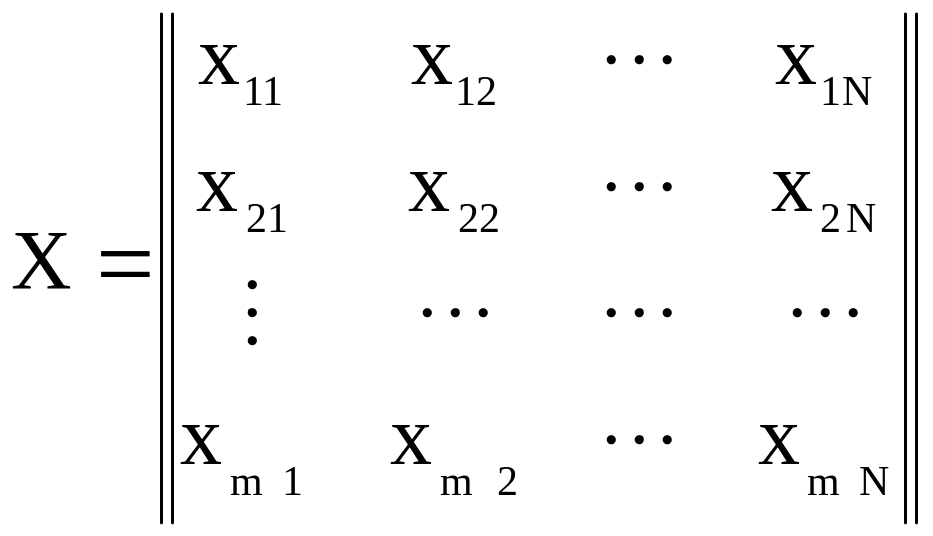
(проведено, например, N опытов)

Заметим, что i – ый столбец матрицы Y – есть значение вектора эндогенных параметров в i – ом опыте. Соответственно i - ый столбец матрицы X есть значение вектора экзогенных параметров в i - ом опыте.

Поэтому с учётом результатов эксперимента и управления (2) имеет место матричное уравнение:

Y = AY + BY + E (5)

Здесь Е – матрица, столбцами которой являются векторы  ‑ ошибок в соответствующих опытах. Для одномерной регрессии аналогом (5) служит линейная модель наблюдений:

Уравнение (5) описывает поведение реальной системы в процессе проведения эксперимента, а уравнение:

(6)

есть математическая модель, предсказывающая значения выходных параметров в процессе проведения эксперимента, т.е. имеет место ситуация, схожая с той, которая изучалась в случае одномерной регрессии. Неприятное отличие состоит в том, что в модели (6) матрица находится как в левой, так и в правой частях уравнения.

Предположим на время, что матрицы А и В известны. Тогда из уравнения (6) находим:

(7)

т.е. матрицу предсказанных значений эндогенных параметров, зависящую от коэффициентов матриц А и В. Из-за наличия матрицы помех Е предсказанные и измеренные значения отличаются друг от друга. В связи с этим возникает следующая оптимизационная задача. Найти элементы , матриц А и В таким образом, чтобы матрица предсказанных выходов наилучшим образом приближала матрицу выходов Y.

Если показателем близости выбирается величина (функционал):

(8)

то требование определения

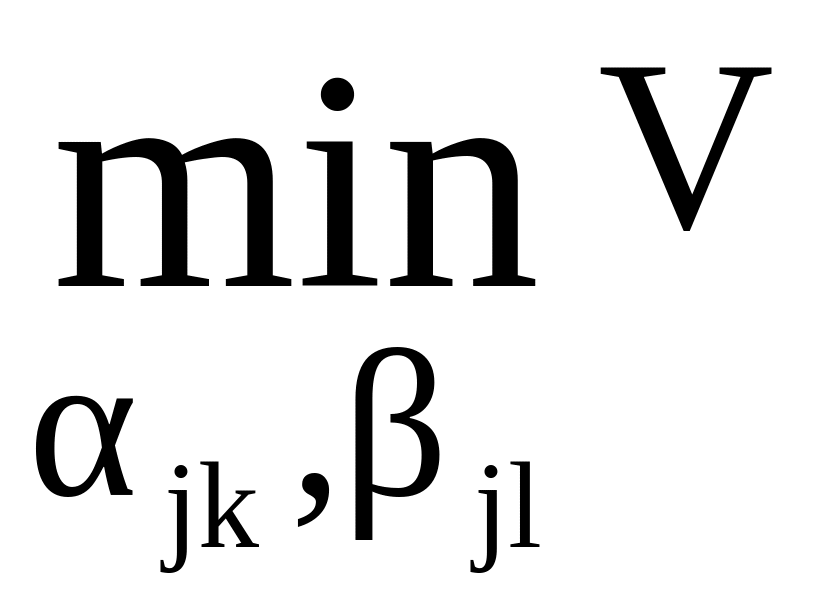(9)

приводит к методу наименьших квадратов.

Определение (9) – трудная задача, т.к. неявно и нелинейно зависит от коэффициентов , в отличии от случая одномерной регрессии.