3. Работа сил электрического поля. Энергия поля системы точечных зарядов.

На положительный точечный заряд q в электрическом поле с напряжённостью E действует сила  F = q E. При перемещении заряда на отрезке dl силами поля совершается работа

dA = F dl = q E dl cos (E, dl).

При перемещении заряда q силами электрического поля на произвольном конечном отрезке из точки 1 в точку 2 эта работа равна

 .

Рассмотрим перемещение точечного заряда q в поле точечного заряда Q, напряженность поля которого 

 .

Проекция отрезка dl на направление вектора E (рис. 1.5) есть dr = dl cos (E, dl).

Работа, совершаемая электрическим полем при перемещении заряда q из точки 1 в точку 2, определяется следующим образом:

Отсюда следует, что работа сил электрического поля не зависит от формы пути, а определяется только начальным и конечным положениями заряда q. Если оба заряда, q и Q, положительны, то работа сил поля положительна при удалении зарядов и отрицательна при их взаимном сближении.

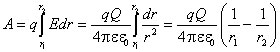
Для электрического поля, созданного системой зарядов Q₁, Q₂,, Q_n, работа перемещения заряда q равна алгебраической сумме работ составляющих сил:

 .

Таким же образом, как и каждая из составляющих работ, суммарная работа зависит только от начального и конечного положений заряда q.

Циркуляция вектора напряженности электрического поля. Работа, совершаемая силами электрического поля при перемещении единичного положительного заряда по замкнутому контуру длиной l, определяется как циркуляция вектора напряженности электрического поля:

Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т.е.

 .

Равенство нулю означает, что силы электрического поля являются силами консервативными, а само поле - потенциальным

Потенциальная энергия заряда q₀ в поле заряда q:

C – значение потенциальной энергии заряда q₀ на дальности, равной бесконечности.

Энергия поля системы точечных зарядов:

ЗАДАЧА № 20:

Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределённым зарядом ( =10 нКл/м). Определить кинетическую энергию T₂ электрона в точке 2, если в точке 1 его кинетическая энергия T₁ = 200 эВ.

Известно, что напряжённость равномерно заряженной бесконечной нити:

Поэтому потенциал поля от равномерно заряженной бесконечной плоскости

где С – постоянная интегрирования.

Тогда разность потенциалов равна:

Электрон, проходя разность потенциалов U, приобретает кинетическую энергию, равную E_к=eU. Т.к. начальная кинетическая энергия равна T₁ , то конечная (согласно закону сохранения) будет равна:

Подставляем числа (переводя одновременно все величины в систему СИ).

График зависимости напряжённости заряженной бесконечной нити от расстояния r:

Вывод: кинетическая энергия электрона в точке 2 равна 400 эВ.