Лабораторная работа №2 Решение и моделирование разностных уравнений

Цель работы – освоение методов решения линейных разностных уравнений и методики моделирования разностных уравнений с помощью инструментариев пакета Matlab

1. Краткие теоретические сведения

Линейное однородное разностное уравнение второго порядка с постоянными коэффициентами имеет вид

. (2.1)

Чтобы подчеркнуть дискретный характер изменения времени, это уравнение часто записывают в форме

. (2.2)

Разностные уравнения третьего и более высоких порядков записываются аналогично. Известны два основных метода решения линейных разностных уравнений – с помощью характеристического полинома и с использованием z-преобразования, аналогичного преобразованию Лапласа.

1.1. Решение разностных уравнений с помощью характеристического полинома.

Найдем решение однородного разностного уравнения в виде , где z – некоторое число. Подставляя x(t) в разностное уравнение (2.1) при f(t)=0 и сокращая на z^t, получаем характеристическое уравнение

.

Если его корни z₁, z₂ вещественные и различные, то общее решение имеет вид

.

Если z₁ = z₂, то в решении появляется линейный множитель

.

В случае пары комплексно-сопряженных корней z_1,2 = i решение может быть записано в вещественной форме

.

Здесь  – модуль комплексного числа z₁, а  – его аргумент.

Формулы для уравнений более высоких порядков выглядят также, просто увеличивается число слагаемых в решении.

Пример 1. Решим разностное уравнение .

Характеристическое уравнение имеет вид .

Его корни вещественные и различные: z₁ = 3, z₂ = 2.

Общее решение: .

Пример 2. Решим разностное уравнение .

Характеристическое уравнение имеет вид .

Его корни комплексные: .

Их положение на комплексной плоскости z_1,2 = i показано на рис. 2.1.

Модуль и аргумент корней можно найти непосредственно на рис. 2.1:

 = 2, . Общее решение: .

Произвольные постоянные с_і находят, задавая начальные условия. Пусть, например, в примере 2 заданы начальные условия х(0)=2; х(1)=4. Записываем общее решение для t=0 и t=1:

.

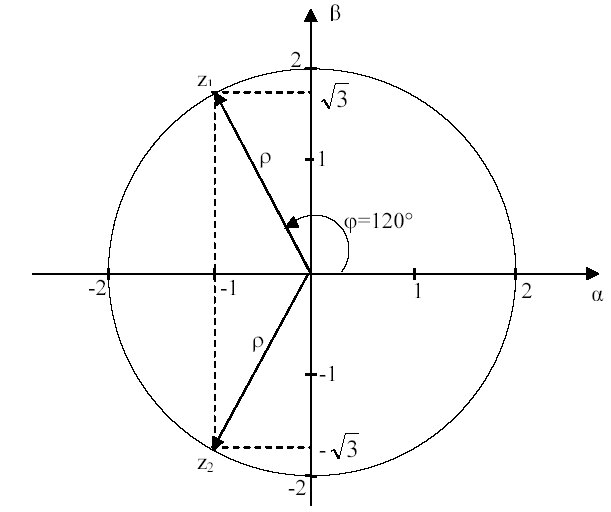
Рис. 2.1. Модуль и аргумент корней

Отсюда находим с₁ = 2, с₂ = 0. Следовательно, решение имеет вид .

Общее решение неоднородного разностного уравнения представляет собой сумму общего решения соответствующего однородного уравнения и любого частного решения неоднородного уравнения. Частное решение ищут в том же виде, что и правая часть, т.е. функция f(t) в уравнении (1):

– если f(t) – постоянная, то в виде константы;

– если f(t) – экспонента, то в виде экспоненты с тем же показателем;

– если f(t) =sin kt или cos kt, то в виде c₁sinkt+c₂coskt.

Коэффициенты с₁ и с₂ находят, подставляя частные решения в разностное уравнение и приравнивая одноименные функции справа и слева.

Пример 3. Дано неоднородное разностное уравнение второго порядка

.

Находим корни характеристического полинома

.

Частное решение ищем в виде х_част=с. Подставляя его в исходное уравнение, находим, что х_част=2.

Общее решение неоднородного уравнения получаем как сумму частного решения и общего решения соответствующего однородного уравнения

.

Коэффициенты с₁, с₂ находим из уравнений 1=2+с₂, , откуда .