Лабораторная работа №1
Исследование процессов квантования и дискретизации на
компьютерных моделях
Цель работы – изучение способов преобразования непрерывных сигналов в дискретные; моделирование процесса квантования по уровню; моделирование процесса квантования по времени; моделирование процесса квантования по уровню и по времени с использованием типовых элементов дискретных САУ пакета прикладных программ
1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1.1. Общие сведения о дискретной сар, квантовании и модуляции
Сигналы, действующие в автоматических системах управления (АСУ), могут быть непрерывными и дискретными. В соответствии с этим АСУ делятся на непрерывные и дискретные.
В непрерывных системах сигналы в процессе их преобразования звеньями системы не прерываются. В дискретных системах имеются звенья, преобразующие непрерывные сигналы в ряд квантованных сигналов или последовательность импульсов.
Процесс преобразования непрерывных сигналов в дискретные называют квантованием. Различают 3 способа квантования:
квантование по времени,
квантование по уровню,
квантование по уровню и времени (смешанное квантование).
В зависимости от способа квантования непрерывного сигнала различают релейные, импульсные и цифровые АСУ.
Техническую процедуру получения последовательности импульсов, несущих информацию о дискретных значениях сигнала, называют модуляцией.
Различают амплитудно-импульсную модуляцию (АИМ), широтно-импульсную (ШИМ), время-импульсную, которая подразделяется на фазо-импульсную (ФИМ) и частотно-импульсную (ЧИМ).
1.2. Структурные схемы дискретных сар
Обобщенные структурные схемы релейной, импульсной и цифровой систем автоматического регулирования (САР) приведены на рис. 1.1 – рис. 1.5.
Рис. 1.1. Структурная схема релейной (двухпозиционной) САР:
РЭ – релейный элемент, НЧ – непрерывная часть
Рис. 1.2. Структурная схема импульсной САР:
ИЭ – импульсный элемент, НЧ – непрерывная часть
Рис. 1.3. Структурная схема амплитудно-импульсного модулятора (АИМ):
ИИМ – идеальный импульсный модулятор, ФЭ – формирующий элемент
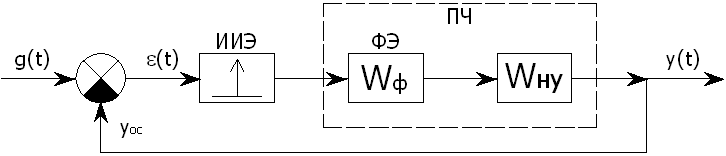
Рис. 1.4. Структурная схема импульсной САР с АИМ:
ИИЭ – идеальный импульсный элемент, ПЧ – приведенная часть
Рис. 1.5. Структурная схема цифровой САР
2. Порядок выполнения работы
2.1. Моделирование процесса квантования по уровню
2.1.1. Для изучения способа квантования по уровню необходимо составить Simulink-модель (далее S-модель), приведенную на рис. 1.6. Блок Quantizer обеспечивает квантование входного сигнала с одинаковым шагом по уровню. Параметр блока Quantization interval – шаг квантования по уровню.
Выполните квантование по уровню с различным шагом (табл. 1.1) и сделайте вывод о его влиянии на отклонение квантованного сигнала от исходного.
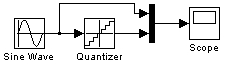
Рис. 1.6. Схема S-модели для изучения квантования по уровню
Таблица вариантов 1.1
№ вар. |
interval 1 |
interval 2 |
interval 3 |
№ вар. |
interval 1 |
interval 2 |
interval 3 |
1 |
0,1 |
0,3 |
0,5 |
11 |
0,4 |
0,6 |
0,8 |
2 |
0,2 |
0,4 |
0,6 |
12 |
1,0 |
1,2 |
1,4 |
3 |
0,3 |
0,5 |
0,7 |
13 |
0,9 |
1,1 |
1,3 |
4 |
0,4 |
0,6 |
0,8 |
14 |
0,5 |
0,7 |
0,9 |
5 |
0,5 |
0,7 |
0,9 |
15 |
0,2 |
0,4 |
0,6 |
6 |
0,6 |
0,8 |
1,0 |
16 |
0,7 |
0,9 |
1,1 |
7 |
0,7 |
0,9 |
1,1 |
17 |
0,9 |
1,1 |
1,3 |
8 |
0,8 |
1,0 |
1,2 |
18 |
0,3 |
0,5 |
0,7 |
9 |
0,9 |
1,1 |
1,3 |
19 |
0,1 |
0,3 |
0,5 |
10 |
1,0 |
1,2 |
1,4 |
20 |
0,6 |
0,8 |
1,0 |
2.1.2. Для изучения двухпозиционного процесса квантования по уровню необходимо составить S-модель, приведенную на рис. 1.7. Релейный блок Relay реализует релейную нелинейность. Параметры: Switch on point – порог включения, Switch off point – порог выключения, Output when on – величина выходного сигнала во включенном состоянии, Output when on – величина выходного сигнала в выключенном состоянии.
Выполните двухпозиционный процесс квантования по уровню с различными параметрами Relay (табл. 1.2) и сделайте вывод о влиянии настроек реле на отклонение квантованного сигнала от исходного. Приведите статическую характеристику работы релейного элемента, используя блок XY Graph.
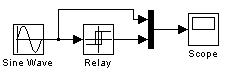
Рис. 1.7. Схема S-модели для изучения двухпозиционного процесса квантования по уровню
Таблица вариантов 1.2
№ вар. |
Switch on |
Switch off |
№ вар. |
Switch on |
Switch off |
1 |
0,1; 0,5 |
-0,1; -0,5 |
11 |
0,9; 1,3 |
-0,9; -1,3 |
2 |
0,2; 0,6 |
-0,2; -0,6 |
12 |
0,8; 1,2 |
-0,8; -1,2 |
3 |
0,3; 0,7 |
-0,3; -0,7 |
13 |
0,7; 1,1 |
-0,7; -1,1 |
4 |
0,4; 0,8 |
-0,4; -0,8 |
14 |
0,6; 1,0 |
-0,6; -1,0 |
5 |
0,5; 0,9 |
-0,5; -0,9 |
15 |
1,0; 1,4 |
-1,0; -1,4 |
6 |
0,6; 1,0 |
-0,6; -1,0 |
16 |
0,5; 0,9 |
-0,5; -0,9 |
7 |
0,7; 1,1 |
-0,7; -1,1 |
17 |
0,1; 0,5 |
-0,1; -0,5 |
8 |
0,8; 1,2 |
-0,8; -1,2 |
18 |
0,2; 0,6 |
-0,2; -0,6 |
9 |
0,9; 1,3 |
-0,9; -1,3 |
19 |
0,3; 0,7 |
-0,3; -0,7 |
10 |
1,0; 1,4 |
-1,0; -1,4 |
20 |
0,1; 0,5 |
-0,1; -0,5 |