Приложение 15 Алгоритм расчета вибрационного смесителя с тороидной камерой

Вибрационный метод смешения различных пищевых сред находит все более широкое применение, что объясняется возможностью совмещения нескольких технологических операций, получения продукта с заранее заданными свойствами, повышением качества смесей.

Предложенная конструкция вибрационного смесителя представляет собой замкнутую рабочую камеру тороидальной формы, упруго подвешенную на цилиндрических пружинах и жесткой раме. Рабочая камера приводится в колебательное движение двумя неуравновешенными массами, вращающимися от стационарно установленного двигателя через гибкий вал. Внутри тороидальной камеры помещен массивный шар, играющий роль дополнительного побудителя движения среды. При обкатывании по внутренней поверхности камеры шар, движущийся синхронно с вибратором, дополнительно измельчает компоненты, турбулизирует поток в канале рабочей камеры. Загрузка компонентов и выгрузка готовой смеси производится через гибкие шланги, снабженные клапанами (например, электромагнитные).

Наличие дебалансного привода с регулируемым эксцентриситетом неуравновешенных масс и упругого подвеса рабочей камеры с изменяющейся жесткостью упругих элементов позволяет в ряде технологических процессов подобрать оптимальный режим работы, при котором возможен непрерывный процесс загрузки и выгрузки. Это дает возможность использовать смеситель в поточных линиях.

Предпосылкой для теоретического исследования движения загрузки по каналу рабочей камеры является задача Н.Е. Жуковского о плоском рассеве, в которой рассмотрено движение свободно лежащей на плоскости частицы при круговых колебаниях в горизонтальной плоскости. Дифференциальные уравнения относительного движения частицы массой m в проекциях на оси ХОY запишутся:

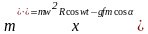; (184)

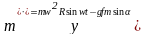. (185)

Где учтем переменную силу инерции 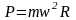и силу трения , направленную противоположно вектору скорости 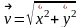в относительном движении и поэтому образующий с осью x угол . – проекция V на ось х; – проекция V на ось y.

Причем ;

.

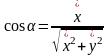Поделим (1) и (1^*) на m и получим:

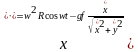; (186)

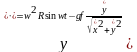. (187)

Частные решения уравнений, соответствующие предельному движению частицы, к которому она стремиться с течением времени:

;

.

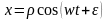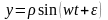Продифференцируем по времени:

;

;

;

.

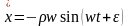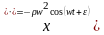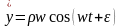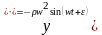Подставим и 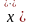в уравнение (184) и преобразуем:

.

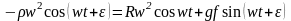Положим

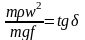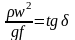или (188)

где 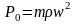– относительная центростремительная сила; – сила трения.

Тогда tg – это есть угол между векторами силы центростремительной при вращении m вокруг т. A с радиусом  и силой трения.

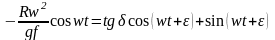
или

.

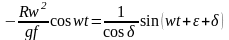Это уравнение обращается в тождество, если

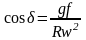(189)

и .

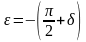Определим из (188)

;

;

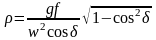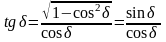и учитывая (189), получим:

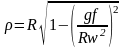(189^**)

где R и w – амплитуда и частота круговых колебаний; f – коэффициент трения частицы о плоскость.

Видимо, когда  становиться равным среднему радиусу тора, то становится возможным движение шарика круговое.

Таким образом, при постоянных w, R и f относительное движение частицы происходит по окружности радиусом  с отставанием по фазе от переносного движения на угол 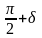. Абсолютное движение происходит также по окружности, причем единственной силой, действующей на частицу в горизонтальной плоскости будет .

Можно также определить значение частоты колебаний плоскости, необходимое для относительного движения частицы по окружности радиусом  ( - радиус рабочей камеры, средний радиус тора).

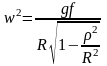(190)

где  – радиус траектории в относительном движении; R – радиус траектории в переносном движении.

В отличии от свободно движущейся частицы центр массы шара в рабочей камере предполагаемого устройства описывает окружность строго заданного радиуса (рис. 119).

Рис. 119. Схема движения частицы в рабочей камере: N_n – нормальная составляющая реакции опор; N_b – составляющая реакции стенки камеры на шарик на ось b; – является ускорением движения плоскости; W_e – ускорение шарика; 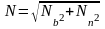; m – масса шарика

Дифференциальные уравнения относительного движения шара массой m в проекциях на естественные оси 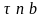имеют вид:

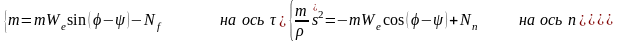(191)

учитывая, что 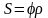, , 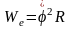, 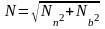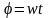преобразуем уравнения (4) к виду:

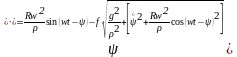(192)

Частное решение уравнений этого вида:

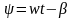(193)

где  – угол сдвига фаз относительного движения центра рабочей камеры.

Продифференцируем его дважды и поставим в уравнение (193), получим:

; ;

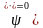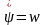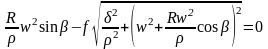.(194)

Приведем его к квадратному уравнению относительно cos:

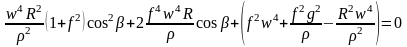.(195)

Решение уравнения (195) имеет вид:

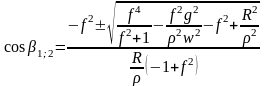.(196)

Отсюда имеем:

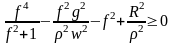.(197)

Из уравнения (197) определяем минимальное значение частоты w, при котором возможно движение шара по круговой траектории:

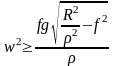. (198)

Сравнение уравнений (190) и (198) показывает, что и в случае свободного движения частицы по плоскости и при движении шара по заданной круговой траектории определяющими параметрами являются приведенный коэффициент сопротивления сдвигу f и соотношение радиусов траекторий переносного и относительного движения.

Анализируя решение уравнения (196) видим, что можно с достаточной степенью точности определить  из выражения:

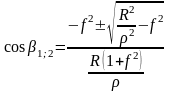(199)

Наличие двух углов сдвига ₁ и ₂ можно объяснить существованием двух равновесных состояний системы при переходе в установившийся режим.

Решая уравнение (195) относительно w, можно выявить зависимость между амплитудой-радиусом R, коэффициентов f и радиусом траектории движения шара :

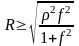. (200)

Таким образом, для данного конкретного размера рабочей камеры, определяемого величиной , можно найти минимальное значение амплитуды R, при которой возможно устойчивое циркуляционное движение шара. Эта величина необходима для выбора режима смешивания.

Сравнение экспериментальных и расчетных значений частоты колебаний  дает хорошую сходимость. Полученные зависимости могут быть использованы для расчета и конструирования вибрационных смесителей такого типа.

Величина амплитуды – радиуса R определяет траекторию движения центра масс рабочей камеры и зависит от жесткостных характеристик упругих элементов системы. Для определения R воспользуемся дифференциальными уравнениями движения центра масс рабочей камеры в установившемся режиме в проекциях на горизонтальные оси x и y (рис. 120):

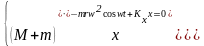(201)

Рис. 120. Движение центра масс рабочей камеры

Обозначим

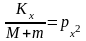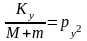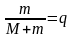; ; (202)

где M – масса рабочей камеры элементами подвеса; m – масса дебаланса; K_x, K_y – жесткость упругих связей в направлении осей x и y; P_x², p_y² – составная частота колебаний.

Решение этой системы уравнений позволяет выделить коэффициенты при тригонометрических функциях с аргументами wt, которые и представляют собой проекции амплитуды-радиуса на оси x и y:

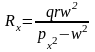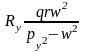и . (203)

Учитывая, что жесткости упругих элементов для рассматриваемой схемы в обоих направлениях равны, имеем 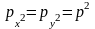. Тогда

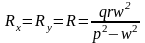. (204)

Выражение (204) позволяет построить R-f(w) и выделить область больших амплитуд, т. е. резонансную область, в которой величина амплитуды колебаний достигает значений . Разделение режима работы дорезонансный и зарезонансный необходимо для анализа усилий, возникающих в элементах вибрационной установки. Зарезонансный режим имеет преимущества перед дорезонансным в отношении нагрузок, передаваемых упругими связями на фундамент машины, что позволяет использовать промышленные помещения с легкими перекрытиями.

В астраханском техническом институте рыбной промышленности и хозяйства разработана и запатентована конструкция вибрациооного смесителя с тороидной рабочесй камерой. (К.Д. Декин, И.Ф. Гончаревич, Н.Н. Корнеева. «Вибрационный смеситель». Патент СССР №1479089 А1, 1980).

ВИБРАЦИОННЫЙ СМЕСИТЕЛЬ

Изобретение относится к химической и пищевой промышленности, в частности к аппаратам, для смешивания жидкостей с сыпучими или вязкими компонентами.

Цель изобретения - повышение качества смешивания компонентов с дифференцированной подачей и обеспечение различной интенсивности воздействия на них.

На рис. 121, а изображен смеситель с дополнительными камерами, смещенными относительно друг друга по высоте; на рис. 121, б – то же, с концентричными дополнительными камерами.

a

б

Рис.121. Вибрационный смеситель

Смеситель включает основную тороидальную камеру 1, дополнительные тороидальные камеры 2 и 3, которые установлены концентрично или cо смещением по высоте относительно друг друга. Камеры 1, 2, и 3 закреплены на раме 4 с помощью упругих элементов, выполненных в виде цилиндрических пружин 5. Дебалансы 6, расположенные на валу 7, соединены с электродвигателем 8 при помощи гибкого вала 9. Внутри камер 1, 2 и 3 помещены рабочие тела в виде шаров 10. Подача компонентов в камеры производится через автономные патрубки 11 ввода, а отвод готовой смеси осуществляется через патрубок 12, при этом патрубки снабжены электромагнитными клапанами 13. Камеры 1, 2 и 3 сообщены между собой каналами 14.

Смеситель работает следующим образом.

При вращении дебалансов 6 камерами 1, 2 и 3 сообщаются круговые или эллиптические колебания, траектория которых зависит от эксцентриситета дебалансных масс и жесткости пружин 5. В каждом конкретном случае может быть подобран оптимальный режим вибрации, обеспечивающий наиболее эффективное перемешивание. Массивные шары 10, помещенные в смесительные камеры 1, 2 и 3, совершают вращательные движения синхронно с дебалансами 6, увлекая и частично измельчая при обкатывании по внутренней поверхности обрабатываемую среду, компоненты которой поступают непрерывно или периодически через патрубки 11 ввода.

Конструкция смесителя позволяет дифференцировать подачу компонентов согласно требованиям технологического процесса. Это необходимо, например, при получении многокомпонентных смесей, в состав которых вхо­дят различные по физическому состоянию и смешиваемой способности материалы. При этом подача компонентов на промежуточных этапах смешивания ведется в непрерывном режиме через патрубки 11, а движение среды из верхних камер в нижнюю осуществляется через каналы 14. Так как пропускная способность каналов 14 устанавливается относительно небольшая, среда совершает несколько оборотов, прежде чем по­падает в другую камеру, вследствие его увеличивается рабочая зона обработки.

Использование изобретения повышает качество смешивания компонентов с дифференцированной подачей и обеспечивает различную интенсивность воздействия на них.