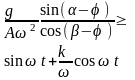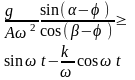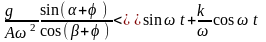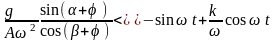Условия движения слоя мелкозернистого материала

Результат выполнения условия	t =
	0…/2	/2…	…3/2	3/2…2
Движение вниз или остановка
Движение вверх

Теоретические исследования движения слоя мелкодисперсного материала вне дна лотка питателя проведем при следующих допущениях. Слой движется как неупругая частица, в момент отрыва имеет скорость, равную вибрационной скорости плоскости, влияние толщины слоя выражается силой сопротивления, пропорциональной скорости движения слоя вне плоскости, при соприкосновении слоя с плоскостью после окончания полета происходит не­упругий удар, и слой мгновенно приобретает скорость плоскости.

Дифференциальные уравнения движения слоя описанного режима имеют вид:

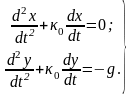
Для выбранных начальных условий решения дифференциальных уравне­ний движения имеют вид

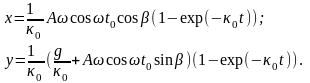(182)

Начало выполнения условий движения слоя вне дна лотка

.

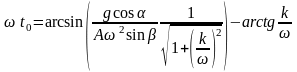Конец выполнения условий движения слоя вне дна лотка

.

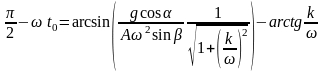При верти­кальном ускорении 18,2 м/с², частоте колебаний =628,3с^-1, если коэффициент сопротивления k больше 2000 с^-1, угол отрыва достигает максимального значению /2, т.е. отделения слоя от дна лотка не происходит.

Выражение, определяющее момент t_п встречи слоя с плоскостью, имею­щее вид

,

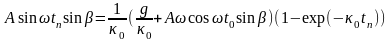может быть решено численно или графически для конкретных значений амплитуды, частоты вибраций и коэффициента сопротивления k₀ при свободном движе­нии.

Для случая, когда слой встречается с плоскостью в момент выполнения условий отрыва 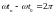, получим оценку вибрационного ускорения, реализующего указанный режим:

.

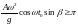Получить численное решение уравнения (182) перемещения для выбранного режима колебаний и физико-механических свойств мелкозернистых частиц сложно ввиду нелинейности и разрывности уравнений движения. На основе экспертных оценок определено, что производительность вибрационного лотка питателя зависит от следующих параметров, расположенных в порядке приоритета: вибрационной скорости А, вибрационного ускорения А² , угла направления колебаний , угла наклона дна лотка к горизонту , поперечного сечения потока сыпучего материала на лотке S, угла трения f сыпучего материала о материал лотка.

Предварительные исследования поведения слоя под воздействием вибрации показали, что на производительность вибрационного лотка влияет проекция вибрационной скорости Acos на поверхность дна питателя. В то же время на сы­пучесть слоя и, как следствие, на производительность лотка оказывает значительное влияние проекция вибрационного ускорения A²sin на нор­маль к поверхности дна питателя. Однако проек­ция гравитационного ускорения gcos на ту же нормаль уменьшает сыпучесть слоя.

Влияние сил трения слоя мелкодисперсных частиц о поверхность дна питателя на производительность можно выразить следующим комплексом: .

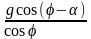Функциональную зависимость производительности q вибрационного лотка представим в таком виде:

.

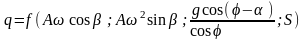Наилучшим образом выбранную функциональную зависимость можно выразить потенциальной зависимостью между параметрами

.

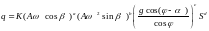Количество критериев в искомом критериальном уравнении можно определить при помощи теоремы Бэкингема, так называемой -теоремы, согласно которой общая функциональная зависимость, связывающая между собой n переменных величин, при составлении которых использованы p первичных единиц измерения, может быть представлена в виде критериальной зависимости между (n-p) критериями подобия или безразмерными комплексами, составленными из величин, входящих в общую функциональную зависимость. В нашем случае n = 5, p = 2, (n - p) = 3.

Составив функциональную зависимость в виде степенной функции, заменим величины формулами размерностей этих величин и, сгруппировав величины по показателям степеней, после преобразований получим критериальное уравнение в виде

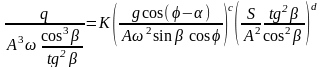.(183)

В уравнении (183) мы образовали безразмерные комплексы, которые позволяют корректно провести эксперименты для вычисления параметров K, c, d.

Для определения параметров K, c, d критериальное уравнение (183) необходимо представить в логарифмическом виде

,

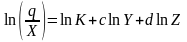где .
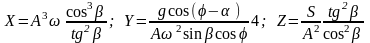