
- •Влияние вибрации на технологические процессы с разработкой методических основ проектирования оборудования
- •240801.65 – Машины и аппараты химических производств
- •150400.68 – Технологические машины и оборудование
- •Введение
- •Глава Колебания и вибрация
- •1.1. Общие сведения о колебаниях и вибрации как о механических явлениях
- •1.2. Использование полезных свойств вибрации
- •1.3. Основные виды процессов и машин, область их применения
- •Глава Виды колебаний
- •2.1. Классификация колебаний
- •2.2. Свободные колебания
- •2.2.1. Общие сведения о свободных колебаниях
- •2.2.2. Свободные колебания системы с одной степенью свободы без трения
- •2.2.3. Свободные колебания, сухое трение
- •Позиционное трение
- •2.2.4. Вязкое трение
- •2.3. Вынужденные колебания
- •Глава Колебательные системы
- •3.1. Виды колебательных систем
- •3.2. Основные характеристики колебательной системы
- •Приведенная жесткость
- •Параллельное соединение
- •Последовательное соединение
- •Приведенные значения
- •Глава IV Основы теории вибрационного перемещения частицы
- •4.1. Эффекты вибрационного перемещения, используемые в технологических процессах
- •4.2. Уравнения движения материальной точки по плоскости, совершающей продольные гармонические колебания, режимы виброперемещения
- •4.3. Условия возникновения движения, асимметрия системы
- •Глава V Экспериментальное исследование процесса виброперемещения слоя насыпного груза
- •5.1. Методики проведения экспериментов
- •5.2. Результаты экспериментальных исследований
- •5.3. Исследование напряженного состояния сыпучего тела
- •Глава VI Математическое моделирование процесса виброперемещения
- •6.1. Механические свойства сыпучих тел
- •Деформация сыпучих тел
- •Сопротивление сыпучего тела сдвигу, внутреннее трение и сцепление.
- •6.2. Свойства обрабатываемых грузов под действием вибрации
- •6.3. Реологические свойства обрабатываемых продуктов
- •6.4. Выбор модели слоя транспортируемого груза
- •6.5. Теоретическое исследование процесса вибрационного перемещения модели слоя сыпучего груза
- •Методика проектирования вибрационных транспортирующих машин
- •Глава VII Вибровозбудители
- •7.1. Классификация вибровозбудителей
- •7.2. Инерционные вибровозбудители
- •7.3. Эксцентриковые вибровозбудители
- •Конструкции вибраторов.
- •7.4. Электромагнитные вибровозбудители
- •7.5. Поршневые вибровозбудители
- •7.6. Высокочастотные вибровозбудители
- •Приложения Приложение 1 Методика расчета центробежных вибровозбудителей
- •Приложение 2 Методика расчета кинематического вибровозбудителя
- •Приложение 3 Методика расчета гидравлического вибровозбудителя
- •Приложение 4 Методика расчета электромагнитного вибровозбудителя
- •Приложение 5 Методика расчета электродинамического вибровозбудителя
- •Приложение 6 Методика расчета виброориентаторов пищевых машин Алгоритм расчета
- •Ориентирование рыбы на наклонном лотке
- •Ориентирование рыбы на планках, движущихся в противофазе
- •Круговой ориентатор
- •Ориентирование рыбы на планках, движущихся в одном направлении с разной интенсивностью
- •Приложение 7 Методика расчета транспортирующих устройств
- •Режимы движения и фазовые углы
- •Приложение 8 Алгоритм расчета виброизоляции набивочной машины для укладки порций рыбы в банки
- •Приложение 9 Алгоритм расчета вибрационного питателя набивочной машины ина-115
- •Приложение 10 Вибрационное уплотнение рыбы
- •Приложение 11 Понятие о динамическом гасителе колебаний
- •Приложение 12 Колебания лопаток турбомашин
- •Приложение 13 Основы расчета виброизоляции
- •Приложение 14 Исследование работы вибрационного питателя с бункером
- •Условия движения слоя мелкозернистого материала
- •Приложение 15 Алгоритм расчета вибрационного смесителя с тороидной камерой
- •Список рекомендуемой литературы
Приложение 14 Исследование работы вибрационного питателя с бункером
Обзор существующих теоретических и практических решений по истечению сыпучих материалов из бункера и работ по вибрационному перемещению слоя мелкозернистого материала позволил сделать следующие выводы. Технологический процесс истечения мелкозернистого материала из бункеров достаточно подробно изучен для бункеров большого объема при естественном истечении, т. е. без вибрационного воздействия на материал. Технологический процесс истечения мелкозернистого материала из малых бункеров под воздействием вибрации через боковую щель изучен недостаточно.
Рассмотренные исследователями процессы истечения из бункера мелкозернистого материала и движение слоя такого материала не связаны в единую цепь, что существенно усложняет дальнейшие исследования и не позволяет разработать стройную методику инженерного расчета рабочих органов дозаторов различных типов - весовых и объемных. Все это затрудняет дальнейшее совершенствование и создание новых конструкций вибрационных питателей.
Задачи исследования технологического процесса вибрационного питателя мелкозернистых материалов с бункером состояли в следующем:
разработать математическую модель процесса подачи сыпучего материала, подвергнутого вибрационному воздействию, к дозирующему устройству из боковой щели бункера;
теоретически исследовать процесс вибрационного перемещения слоя сыпучего материала при повышенной частоте вибрации и обосновать режимы работы и параметры вибрационного привода питателя;
получить зависимость производительности вибрационного питателя от параметров вибрации и физико-механических свойств сыпучего материала на основе теории размерностей;
В качестве рабочей гипотезы было принято, что мелкозернистый материал в бункере под воздействием вибрации представляет собой «псевдожидкость». Такая гипотеза позволяет применить гидромеханические законы истечения материала из бункера.
Система бункер - вибрационный лоток представляет собой, обычно, бункер прямоугольного сечения со щелью во всю ширину бункера (рис. 118), дном которого является лоток, приводящийся в колебательные движения тем или иным способом. Наиболее часто лоток соединен с бункером с помощью плоских пружин или шарниров и приводится в колебательные движения кривошипным механизмом или электромагнитами. Колебания лотка активизирует сыпучий зернистый материал, поведение которого можно уподобить поведению вязкой жидкости. Поскольку в случае сыпучего материала нарушаются некоторые допущения, принятые при определении понятия вязкости жидкости или газа, то многие исследователи сыпучую среду из мелкозернистого материала под воздействием вибрации представляют как «псевдожидкость».

Рис. 118. Схема бункера с лотком
Исследуем динамику истечения мелкозернистого материала из бункера, используя аппарат дифференциальных уравнений. Для большей общности, предположим, что в бункер постоянно подается мелкозернистый материал с произвольной интенсивностью q м/с. Допустим, что h – напор в горизонтальном сечении бункера, проходящем через геометрический центр отверстия, отвечающий установившемуся движению, т.е. такой, что при этом напоре расход сыпучего материала через отверстие в точности равен притоку q. Тогда
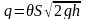 .
.
Рассматривая элементарный баланс сыпучего материала в бункере в течение малого промежутка времени dt, получаем дифференциальное уравнение, связывающее высоту материала в бункере Н и время истечения t, которое после разделения переменных имеет вид
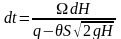 .
.
Частное решение дифференциального уравнения истечения мелкозернистого материала из бункера под воздействием вибрации имеет вид
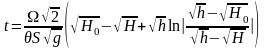 .
.
Напор равновесия h физически представляет собой точку подачи материала. Если исходный напор H0 меньше (больше), чем напор равновесия h, то фактический расход из отверстия будет увеличиваться (уменьшаться) с течением времени. Соответственно, Н будет замедленно возрастать (убывать), приближаясь к равновесному значению h. В частном случае, когда притока сыпучего материала в бункер нет, т. е. h = 0, легко получить явное представление для функции H(t):
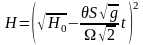 .
.
Перемещение слоя мелкодисперсного материала исследуем при допущениях, что дно вибрирующего лотка представляет собой плоскость, совершающую гармонические колебания. Направление колебаний составляет угол к плоскости. Сама плоскость наклонена под углом к горизонту. Движение слоя мелкодисперсного материала под воздействием вибрации отличается от движения отдельной частицы. Этим отличиям способствует форма и размер частиц, образующих слой, толщина слоя, влажность частиц, их упругие свойства, воздухопроницаемость слоя, характер взаимодействия материала, из которого состоит слой, и материала поверхности, внутреннее трение и силы взаимодействия между частицами. Эти свойства слоя начнут проявлять себя при его движении, как только его толщина станет более, чем размер одной частицы.
Все факторы, влияющие на движение слоя, были представлены силой Ф сопротивления движению, пропорциональной вибрационной скорости,
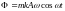 .
.
В таком случае дифференциальные уравнения движения слоя мелкодисперсных частиц по колеблющейся поверхности лотка питателя примут вид
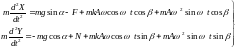
Направление действия силы трения F зависит от направления относительной скорости движения слоя, и это приводит к появлению различных видов перемещения слоя: движение вместе с плоскостью (остановку), движение "по" и "против" направления оси абсцисс и движение вне плоскости.
Для получения численных значений перемещения и скорости движения слоя интегрировать дифференциальные уравнения движения с учетом переменного направлением действия сил трения F и сопротивления Ф необходимо по моментам перехода от одного вида движения к другому.
Уравнение движения слоя мелкозернистых материалов по дну вибрационного после интегрирования лотка имеет вид
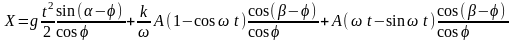 .
.
В табл. 2 представлены условия движения слоя мелкозернистого материала. Правые части условий зависят от угла колебаний t и коэффициента k, а левые части представляют собой постоянные величины, определяемые конструктивными параметрами вибрационного лотка и коэффициента трения материала о поверхность лотка.
Таблица 2
