
- •Влияние вибрации на технологические процессы с разработкой методических основ проектирования оборудования
- •240801.65 – Машины и аппараты химических производств
- •150400.68 – Технологические машины и оборудование
- •Введение
- •Глава Колебания и вибрация
- •1.1. Общие сведения о колебаниях и вибрации как о механических явлениях
- •1.2. Использование полезных свойств вибрации
- •1.3. Основные виды процессов и машин, область их применения
- •Глава Виды колебаний
- •2.1. Классификация колебаний
- •2.2. Свободные колебания
- •2.2.1. Общие сведения о свободных колебаниях
- •2.2.2. Свободные колебания системы с одной степенью свободы без трения
- •2.2.3. Свободные колебания, сухое трение
- •Позиционное трение
- •2.2.4. Вязкое трение
- •2.3. Вынужденные колебания
- •Глава Колебательные системы
- •3.1. Виды колебательных систем
- •3.2. Основные характеристики колебательной системы
- •Приведенная жесткость
- •Параллельное соединение
- •Последовательное соединение
- •Приведенные значения
- •Глава IV Основы теории вибрационного перемещения частицы
- •4.1. Эффекты вибрационного перемещения, используемые в технологических процессах
- •4.2. Уравнения движения материальной точки по плоскости, совершающей продольные гармонические колебания, режимы виброперемещения
- •4.3. Условия возникновения движения, асимметрия системы
- •Глава V Экспериментальное исследование процесса виброперемещения слоя насыпного груза
- •5.1. Методики проведения экспериментов
- •5.2. Результаты экспериментальных исследований
- •5.3. Исследование напряженного состояния сыпучего тела
- •Глава VI Математическое моделирование процесса виброперемещения
- •6.1. Механические свойства сыпучих тел
- •Деформация сыпучих тел
- •Сопротивление сыпучего тела сдвигу, внутреннее трение и сцепление.
- •6.2. Свойства обрабатываемых грузов под действием вибрации
- •6.3. Реологические свойства обрабатываемых продуктов
- •6.4. Выбор модели слоя транспортируемого груза
- •6.5. Теоретическое исследование процесса вибрационного перемещения модели слоя сыпучего груза
- •Методика проектирования вибрационных транспортирующих машин
- •Глава VII Вибровозбудители
- •7.1. Классификация вибровозбудителей
- •7.2. Инерционные вибровозбудители
- •7.3. Эксцентриковые вибровозбудители
- •Конструкции вибраторов.
- •7.4. Электромагнитные вибровозбудители
- •7.5. Поршневые вибровозбудители
- •7.6. Высокочастотные вибровозбудители
- •Приложения Приложение 1 Методика расчета центробежных вибровозбудителей
- •Приложение 2 Методика расчета кинематического вибровозбудителя
- •Приложение 3 Методика расчета гидравлического вибровозбудителя
- •Приложение 4 Методика расчета электромагнитного вибровозбудителя
- •Приложение 5 Методика расчета электродинамического вибровозбудителя
- •Приложение 6 Методика расчета виброориентаторов пищевых машин Алгоритм расчета
- •Ориентирование рыбы на наклонном лотке
- •Ориентирование рыбы на планках, движущихся в противофазе
- •Круговой ориентатор
- •Ориентирование рыбы на планках, движущихся в одном направлении с разной интенсивностью
- •Приложение 7 Методика расчета транспортирующих устройств
- •Режимы движения и фазовые углы
- •Приложение 8 Алгоритм расчета виброизоляции набивочной машины для укладки порций рыбы в банки
- •Приложение 9 Алгоритм расчета вибрационного питателя набивочной машины ина-115
- •Приложение 10 Вибрационное уплотнение рыбы
- •Приложение 11 Понятие о динамическом гасителе колебаний
- •Приложение 12 Колебания лопаток турбомашин
- •Приложение 13 Основы расчета виброизоляции
- •Приложение 14 Исследование работы вибрационного питателя с бункером
- •Условия движения слоя мелкозернистого материала
- •Приложение 15 Алгоритм расчета вибрационного смесителя с тороидной камерой
- •Список рекомендуемой литературы
Приложение 9 Алгоритм расчета вибрационного питателя набивочной машины ина-115
Достоинства вибрационных уплотняющих машин.
Разработано и используется много различных конструкций машин для уплотнения рыбы в тару различной вместимости. Широкое использование уплотняющих машин объясняется тем, что они при своей относительной простоте конструкции и надежности обеспечивают многократное повышение производительности труда. Процесс работы этих машин изучен далеко не достаточно. Практически не рассматривался процесс уплотнения рыбы с позиций моделирования ее большой неоднородной массы, обладающей упругими, вязкими, пластическими и адгезионными свойствами, и не была исследована динамика уплотняющих машин (вопросы уравновешивания и демпфирования). Недостаточно исследованы вопросы ориентирования внутри тары при различных видах колебаний. Большие резервы повышения эффективности работы этих машин лежат при выборе оптимального закона и режима колебаний. При условии, если эти исследования будут носить комплексный характер, т.е. с механической и технологической позиций, можно ожидать положительных эффектов по улучшению технологии, качества просаливания, длительности хранения, обеспечения лучшего товарного вида.
Краткое описание устройства и принципа действия набивочной машины ИНА-115.
Машина предназначена для укладки рыбы в банки и инвентарные формы. При замене рыбоводов ее можно использовать на любом по размеру сырье.
Машина имеет сменные рыбоводы, каждый рыбовод предназначен для определенных видов рыб. Однотрубный рыбовод в верхней части имеет расширение для облегчения загрузки, в нижней – сужение для жгутообразования и уплотнения. В трехтрубном рыбоводе загрузочная часть образуется тремя патрубками, сходящимися к жгутообразующей части. Нижняя часть рыбовода является калибрующей частью и имеет цилиндрическую форму. Четырехтрубный рыбовод используется при работе машины на скумбрии, ставриде, сардинелле, сельди.
Колебательное движение рыбовода осуществляется с помощью эксцентрикового механизма. Рыбовод крепится к раме вибратора, которая связана подвижными осями с четырьмя штангами, шарнирно закрепленными на раме машины. Амплитуда колебаний рыбовода – 6 мм, частота колебаний регулируется с помощью вибратора от 200 до 600 Гц; этот диапазон позволяет выбрать оптимальный режим работы машины для различных видов рыбы.
Вращающийся с выстоями операционнный стол имеет 4 цилиндра, в которых движутся четыре подпружиненных поршня.
Поворот операционного стола, порционирующего ножа, перемещение копира, вращение кантователя, движение механизма подачи и съема банок осуществляется от общего электродвигателя через главный распределительный вал.
Кантователь за два цикла поворачивает наполненную банку из положения дном вниз и банка выталкивается в течку, поступая на дальнейшую обработку.
Алгоритм расчета вибрационного питателя набивочной машины ИНА-115.
С точки зрения динамики процесса набивочную машину ИНА-115 можно представить в виде колебательной (двухмассовой ) системы, в которой характер движения масс рабочих органов питателя определяется как геометрическими, так и динамическими параметрами системы.
Особенностью большинства конструкций вибрационных питателей является применение резонансного принципа действия, при котором малой возмущающей силой вибратора возможно развить на рабочем органе значительные усилия.
Вибрационный питатель (рыбовод) может быть представлен в виде модели двухмассовой системы с двумя степенями свободы (рис. 110).

Рис. 110. Двухмассовая
модель питателя:
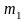 – рыбовод с рыбой, расположенный на
упругих подвесках, жесткостью
– рыбовод с рыбой, расположенный на
упругих подвесках, жесткостью
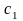 ;
;
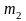 – представляет собой основание рыбовода:
стол - карусель с дозирующими стаканами,
передаточные и образующие механизмы
– представляет собой основание рыбовода:
стол - карусель с дозирующими стаканами,
передаточные и образующие механизмы
Для уменьшения
вибрации и шума масса
располагается на подвесках малой
жесткости
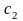 .
.
Жесткости
и
имеют соотношение
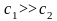 .
.
На каждую массу действуют возмущающие усилия вибратора, равные по модулю и противоположные по фазе.
На массу
,
представляющую рыбовод с рыбой, действуют:
сила инерции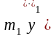 ,
возмущающая сила
,
возмущающая сила
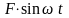 ,
сила упругости
,
сила упругости
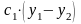 .
.
На массу
,
представляющую саму машину действуют:
сила инерции
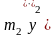 ,
возмущающая сила
,
сила упругости от массы
,
возмущающая сила
,
сила упругости от массы
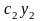 ,
сила упругости от массы
,
сила упругости от массы
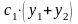 .
.
Проецируем эти силы для каждой массы на вертикальную ось (в направлении которой происходят колебания), получим дифференциальные уравнения для каждой массы из условия статического равновесия сил.
Дифференциальные уравнения движения для обеих масс, находящихся под действием гармонической возмущающей силы будут иметь вид:
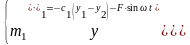 (113)
(113)
Для упрощения уравнений введем обозначения
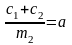 ;
;
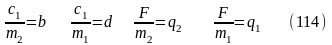
Частное решение уравнений примем в виде
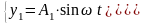 (115)
(115)
где
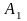 – амплитуда колебаний рыбовода;
– амплитуда колебаний рыбовода;
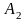 – амплитуда колебаний основания машины.
– амплитуда колебаний основания машины.
Подставляя выражения (114) и (115) в (113) получим:
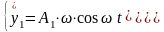 (116)
(116)
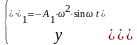 (117)
(117)
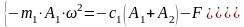 (118)
(118)
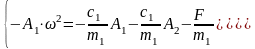 (119)
(119)
Подставляя в (119) обозначения (114), получим:
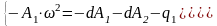 (120)
(120)
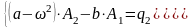 (121)
(121)
Для нахождения
отношения амплитуд
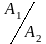 из выражений (121) определим значения
и
.
из выражений (121) определим значения
и
.
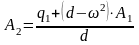 (122)
(122)
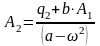 .
(123)
.
(123)
Приравниваем правые части уравнений (122) и (123) и находим
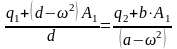 (124)
(124)
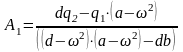 .
(125)
.
(125)
Подставив значения из выражения (125) в (124), получим:
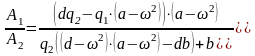 (126)
(126)
Выражение (126) получено с учетом (125) и (123)
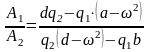 (127)
(127)
Подставив в
уравнение (127) обозначения (114), и поделив
числитель и знаменатель на
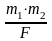 ,
получим:
,
получим:
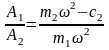 (128)
(128)
Частное уравнение
системы получается следующим образом.
При устранении возмущающей силы, т. е.
при
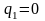 и
и
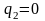 ,
из уравнений (122) получим:
,
из уравнений (122) получим:
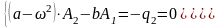 .
(129)
.
(129)
Уравнения (129) могут дать для и отличные от нуля решения, если определитель системы уравнений равен 0.
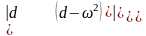 .
(130)
.
(130)
Разворачивая определитель, получим уравнение (131)
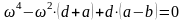 .
(131)
.
(131)
Биквадратное уравнение (131) называется частотным уравнением системы
;
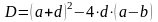 ;
;
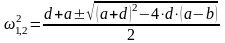 ;
;
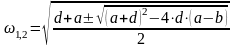 .
(132)
.
(132)
Подставляя в уравнение (132) обозначения (114), получим
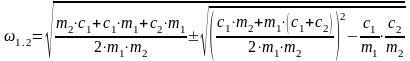 (133)
(133)
Жесткость нижних
пружин
,
устанавливаемых для амортизации,
выбирается значительно меньше жесткости
основных подвесок
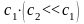 .
Поэтому с достаточной для практики
точностью можно принять
.
Поэтому с достаточной для практики
точностью можно принять
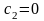 ,
тогда из уравнения (21)
,
тогда из уравнения (21)
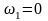 .
.
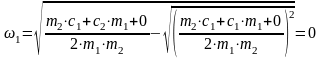 (134)
(134)
Вторая собственная частота колебаний будет равна
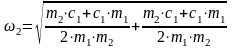 (135)
(135)
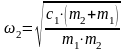 (136)
(136)
где
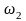 – собственная частота колебаний машины,
рад/сек;
– собственная частота колебаний машины,
рад/сек;
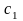 – общая жесткость упругих подвесок
рыбовода, кг/с2;
– масса рыбовода с рыбой, кг;
– масса машины, кг.
– общая жесткость упругих подвесок
рыбовода, кг/с2;
– масса рыбовода с рыбой, кг;
– масса машины, кг.
Определим А2 – амплитуду колебаний машины.
Подставив
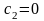 в формулу (16), получим
в формулу (16), получим
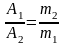 (137)
(137)
Из уравнения (137) выразим А2.
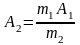 (138)
(138)
где
– масса рыбовода с рыбой, кг;
– масса машины, кг;
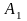 – амплитуда колебаний рыбовода.
– амплитуда колебаний рыбовода.
Из уравнения (137) видно, что амплитуды вынужденных колебаний обратно пропорциональны величинам масс систем. Введем обозначение:
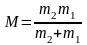 (139)
(139)
где М – приведенная масса системы, кг.
Тогда уравнение (136) можно записать в виде
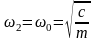
где – собственная частота колебаний системы; – есткость упругих подвесок чаши питателя.
Таким образом, дифференциальные уравнения двухмассовой системы вибровозбудителя с двумя степенями свободы можно свести к уравнению движения одномассовой системы с одной степенью свободы.

Рис. 111. Одномассная
модель питателя с введением в систему
сил сопротивления
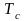 .
.
Силы сопротивления, действующие на колебательную систему рыбовода, состоят из сил внутреннего сопротивления в материале упругих подвесок и сил внешнего сопротивления – сил трения тушек кильки о внутренние стенки рыбовода.
Рассмотрим суммарную силу всех сопротивлений, действующих в системе, как эквивалентную вязкому сопротивлению, и, следовательно, пропорциональную первой степени скорости смещения.
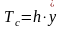
где
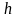 – коэффициент сопротивления;
– коэффициент сопротивления;
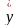 – скорость смещения.
– скорость смещения.
Составим уравнение вынужденных колебаний одномассной системы из условия равновесия сил.
На
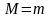 приведенную массу системы действует
сила инерции
приведенную массу системы действует
сила инерции
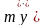 ,
суммарная сила сопротивления, эквивалентная
вязкому сопротивлению
,
сила упругости
,
суммарная сила сопротивления, эквивалентная
вязкому сопротивлению
,
сила упругости
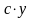 ,
возмущающая сила
,
возмущающая сила
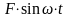 .
.
Уравнение вынужденных колебаний одномассной системы имеет вид:
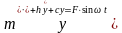 (140)
(140)
разделим уравнение (140) на
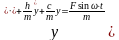 (141)
(141)
Зная, что
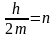 -
коэффициент затухания, а
-
коэффициент затухания, а
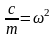 ,
получим
,
получим
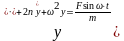 (142)
(142)
Общее решение дифференциального уравнения (30) имеет вид:
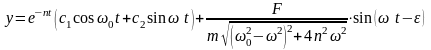 (143)
(143)
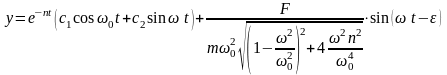 (144)
(144)
Если пренебречь затухающими колебаниями, имеющими значение лишь в начале движения, то перемещение колеблющейся массы при установившихся вынужденных колебаниях определяется уравнением:
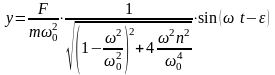 (145)
(145)
т.
к.
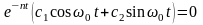
где – частота собственных колебаний системы; – частота вынужденных колебаний; – угол сдвига фаз между перемещением и внешней силой.
Угол определяется из соотношения
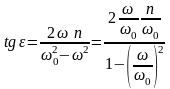 ;
(146)
;
(146)
обозначив
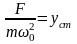 и подставив в формулу (145) получим
и подставив в формулу (145) получим
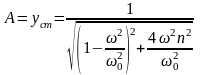 (147)
(147)
где
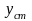 – статическое смещение, которое
получилось бы при статическом приложении
силы F.
– статическое смещение, которое
получилось бы при статическом приложении
силы F.
Отношение
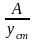 называется
динамическим коэффициентом.
называется
динамическим коэффициентом.
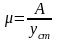 (148)
(148)
Выражение для динамического коэффициента получается из формулы (147)
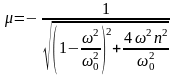 .
(149)
.
(149)
Величина
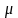 зависит от отношения
зависит от отношения
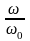 угловых частот возмущающей силы и
свободных колебаний без затухания, а
также от отношения
угловых частот возмущающей силы и
свободных колебаний без затухания, а
также от отношения
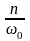 ,
которое практически в большинстве
случаев мало.
,
которое практически в большинстве
случаев мало.
Свойство кривых, получающихся при значениях динамического коэффициента в зависимости от при различных значениях затухания, характеризуемого величиной , называется частотными характеристиками или резонансными кривыми колебательной системы.
Если затухание в системе не велико, то по мере возрастания частоты возмущающей силы динамический коэффициент, а, следовательно, и амплитуда колебаний увеличивается.
Максимум
динамического коэффициента несколько
смещен в сторону от абсциссы
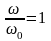 .
Однако это смещение мало и можно
приближенно определить
.
Однако это смещение мало и можно
приближенно определить
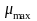 ,
подставив в формулу (149)
,
подставив в формулу (149)
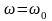 .
.
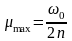 .
(150)
.
(150)
Очевидно, что максимум динамического коэффициента обратно пропорционален коэффициенту затухания n. Максимальная амплитуда колебаний определяется выражением:
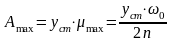 .
(151)
.
(151)
Область увеличения
амплитуд, где
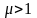 ,
называется областью резонанса.
,
называется областью резонанса.
Резонансной частотой называется частота внешней силы, совпадающая с частотой собственных колебаний системы.
Для определения мощности, требуемой для преодоления силы сопротивления, рассмотрим работу, производимую возмущающей силой за цикл в процессе установившихся вынужденных колебаний.
Перемещение точки приложения возмущающей силы:
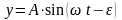 .
(152)
.
(152)
Скорость точки приложения возмущающей силы:
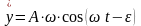 .
(153)
.
(153)
Поэтому работа
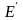 ,
произведенная за период колебаний
,
произведенная за период колебаний
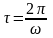 будет равна:
будет равна:
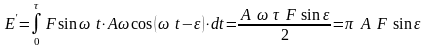 .(154)
.(154)
Эта работа должна
быть равна энергии
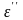 ,
рассматриваемой вследствие действия
силы вязкого сопротивления
,
рассматриваемой вследствие действия
силы вязкого сопротивления
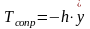 за тот же промежуток времени. Умножая
силу сопротивления
за тот же промежуток времени. Умножая
силу сопротивления
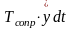 и интегрируя в интервале от 0 до
и интегрируя в интервале от 0 до
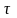 ,
получаем для рассеиваемой за цикл
энергии выражения:
,
получаем для рассеиваемой за цикл
энергии выражения:
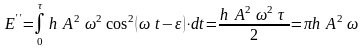 (155)
(155)
Приравнивая
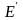 и
и
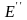 ,
получаем уравнение для определения
амплитуды возмущающей силы
:
,
получаем уравнение для определения
амплитуды возмущающей силы
:
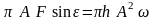 (156)
(156)
Выражаем из уравнения амплитуду возмущающей силы окончательно получаем:
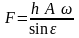 ;
(157)
;
(157)
т. к.
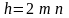 ,
то
,
то
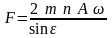 .
(158)
.
(158)
Средняя мощность , необходимая для преодоления силы сопротивления определяется по формуле
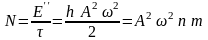 .
(159)
.
(159)
