Приложение 8 Алгоритм расчета виброизоляции набивочной машины для укладки порций рыбы в банки

Набивочная машина имеет рыбовод 1, к которому вертикальные колебания передаются от эксцентрикового механизма 2. Рыбовод установлен на пружинном кронштейне 3, закрепленном на стойке 4. Привод осуществляется от электродвигателя 7, через вариатор 6 и ременную передачу 5. Все устройство крепится на основании 8, установленном на виброизоляторах 9. Набивочная машина установлена посредине пролета на двух двутавровых балках.

Рис. 108. Схема привода в движение рыбовода набивочной машины: 1 – рыбовод, 2 – эксцентриковый механизм, 3 – кронштейн пружины, 4 – стойка, 5 – цепная передача, 6 – вариатор, 7 – электродвигатель, 8 – основание машины, 9 – виброизолятор

Машина расположена на расстоянии 1/3 L от стенки (а = L/3).

Определим величину прогиба балок от единичной силы по формуле (78):

y₁=F1/K₁ (78)

где y₁ – величина прогиба балок от единичной силы, м; F1 – единичная сила (F1=1 Ньютон); K₁ – жесткость балки, н/м.

Рис. 109. Расчетная схема расположения набивной машины относительно стенок

Жесткость балки определяется по формуле (2):

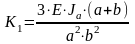(79)

где Е – модуль упругости материала балки, Е = 210⁷ н/см²; J_a – момент инерции балки, см⁴; L – длина пролета, м; a, b – расстояние от стенок здания до машины, м.

Определим собственную частоту колебаний системы по уравнению 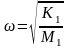(80):

(80)

где  – собственная частота колебаний системы, Гц; К₁ – жесткость балки, н/м; М₁ – приведенная масса системы, кг;

М₁ = М + М_о,

где М – масса рыбовода набивочной машины, кг; М_о – масса основания, кг.

Определим коэффициент динамичности системы по формуле 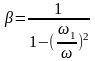(81):

(81)

где ₁ – возмущающая частота колебаний системы;  – собственная частота колебаний системы, Гц.

Силу, возникающую вследствие вынужденных колебаний системы, рассчитываем по формуле 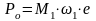(82):

(82)

где Р_о – сила, возникающая вследствие вынужденных колебаний системы, Н; М₁ – приведенная масса системы, кг; ₁ – возмущающая частота колебаний системы, Гц; е – радиус кривошипа эксцентрикового механизма, м. Определяется по формуле (83):

е=А/2 (83)

где А – амплитуда колебаний, м.

С помощью уравнений приводим нагрузку от набивочной машины к статической:

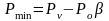(84)

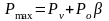(85)

где P_v – сила веса машины, Н.

P_v = M₁g (86)

g = 9,81 м/с²;

Р_о – сила, возникающая вследствие вынужденных колебаний системы, Н;

 – коэффициент динамичности системы.

Изгибающие моменты, действующие на балку, определяются по формулам (10) и (11), (Нм):

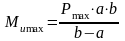(87)

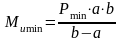(88)

где P_max, P_min – максимальная и минимальная статическая нагрузка от набивочной машины, Н;

a, b – расстояние от стенок здания до машины, м.

Напряжение в двутавровой балке от изгибающих моментов (Нм²) определим по формуле:

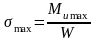; (89)

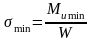(90)

где M_{u max}, M_{u min} – максимальный и минимальный изгибающие моменты, действующие на двутавровую балку, Нм²; W – момент сопротивления сечения профиля двутавровой балки, см³.

Условие прочности данной системы будет иметь вид:

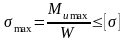(91)

где [] – допускаемое напряжение в двутавровой балке, Нм.

Мощность привода колебательной системы определяем по эмпирической формуле, Вт:

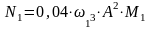, (92)

где А – амплитуда колебаний, м; М₁ – приведенная масса системы, кг; ₁ – возмущающая частота колебаний системы, Гц.

Мощность электродвигателя (Вт) определим по формуле:

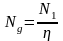(93)

где  – общий КПД привода.

Общий КПД привода определяется по формуле:

=₁₂₃ (94)

где ₁ – КПД вариатора; ₂ – КПД цепной передачи; ₃ – КПД подшипников.

Амплитуда вынужденных колебаний системы в вертикальной плоскости под действием динамической силы определяем из уравнения:

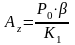(95)

где К₁ – жесткость балки, Н/м; Р₀ – сила, возникающая вследствие вынужденных колебаний системы, Н;  – коэффициент динамичности системы; A_z – амплитуда вынужденных колебаний системы, м.

Для уменьшения амплитуды вынужденных колебаний системы установим виброизоляторы.

Жесткость (Н/м) всех виброизоляторов в вертикальном направлении вычислим по формуле:

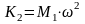(96)

Жесткость всей системы рассчитывается с учетом жесткости балок и виброизоляторов.

Рассчитываем жесткость одного виброизолятора, приняв число виброизоляторов равным z = 4–14, по формуле (20):

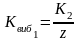(97)

Темп нарастания угловой скорости определяем по формуле (21), с^–2:

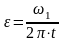(98)

где t – время разгона.

Время разгона принимается равным t = 0,5–2 сек.

Для выбора типа виброизоляторов пружинных или резиновых определим коэффициент демпфирования по формуле 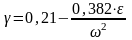(99):

(99)

при 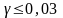– применяются стальные пружины; 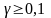– применяются резиновые амортизаторы; 0,03    0,1 – применяются комбинированные амортизаторы.

Определим статическую нагрузку на одну пружину, Н:

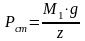(100)

где M₁ – приведенная масса системы, кг; z – число пружин.

Динамическая нагрузка на одну пружину определяется по формуле (101), Н:

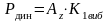(101)

где А_z – амплитуда вынужденных колебаний системы в вертикальной плоскости, мм; К₁ – жесткость одного виброизолятора, Н/м.

Определим расчетную нагрузку на одну пружину по формуле (102):

Р_пр1 = Р_ст + 1,5Р_ин (102)

где 1,5 – коэффициент запаса.

Диаметр проволоки пружины вычислим по формуле:

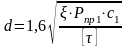(103)

где с₁ = D/d – отношение среднего диаметра пружины к диаметру проволоки, дается в пределах с₁ = 4–10;  – коэффициент формы сечения и кривизны витка, который определяется по формуле (104):

(104)

[] – предел текучести, Н/мм².

Целесообразно применение пружин изготовленных их материалов выдерживающих ударные нагрузки. Например, 60С2, 60С2Н2А, 50ХФА.

Число рабочих витков пружины находим по формуле:

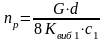(105)

где G – модуль упругости материала пружины при сдвиге, Н/мм².

Модуль упругости материала пружины при сдвиге определим по формуле (106):

(106)

где Е – модуль упругости материала пружины, Н/см²;  – коэффициент Пуассона для стали, =0,3.

Определим высоту нагруженной пружины с учетом поджатия и обработки ее концов по формуле:

H = n_ph + (n_g+0,5) d (107)

где n_g – дополнительное число витков, принимается равным: при n_p  7, то n_g =1,5;n_p  7, то n_g = 2,5; h – шаг витков пружины, выбирается в пределах 0,25–0,5.

При расчете резиновых виброизоляторов находим площадь их поперечного сечения по выражению, м²:

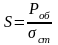(108)

где Р_об – нагрузка на все виброизоляторы, Н; _ст – статическое напряжение в резине, которое рекомендуется принимать от 0,1 до 0,5 мН/м².

Размеры сечений резиновых виброизоляторов и их число выбираем по формуле в зависимости от конфигурации:

для квадратного сечения

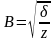(109)

где S – площадь поперечного сечения, м².

Для круглого сечения

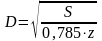(110)

где В – сторона квадрата, м; D – диаметр сечения виброизолятора, м.

Рабочая высота виброизолятора находится по выражению:

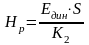(111)

где Е_дин – динамический модуль упругости резины, Е_дин= 2–10 Н/м²; S – площадь поперечного сечения виброизолятора, м²; К₂ – жесткость всех виброизоляторов, Н/м.

Поперечный размер виброизолятора должен находиться в пределах:

Н_р  В (или D)  1,5Н_р (112)

Число виброизоляторов должно находиться в пределах:

– для квадратного сечения

;

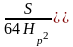– для круглого сечения

.
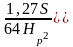