Приложения Приложение 1 Методика расчета центробежных вибровозбудителей

Центробежные вибровозбудители являются безударными вибрационными машинами (исполнительный орган машины вибрирует, не ударяясь о другие элементы машины).

Задачи расчета параметров вибрационных машин довольно разнообразны. Большая часть их специфична: она определена особенностями технологического процесса, выполняемого машиной, видом используемого вибропривода, конструктивными особенностями машины.

В качестве модели вибрационной машины возьмем систему с сосредоточенными параметрами в виде линейной системы с одной степенью свободы, определяемой координатой исполнительного органа и его массой m₁ (рис. 92).

Рис. 92. Расчетная схема вибровозбудителя с центробежным возбуждением вибрации

Исполнительный орган совершает вынужденную вибрацию под действием периодической вынуждающей силы F(t) и имеющей период 2/, сил упругости пружины 2 с коэффициентом жесткости c и демпфера 5 с коэффициентом сопротивления b.

Пружины и демпфер моделируют взаимодействия исполнительного органа с обрабатываемой средой.

Среднее значение мощности, необходимой для поддержания установившейся периодической вибрации в такой системе:

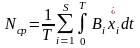; Вт

где – период вибрации, 1/с; 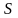– общее число действующих в системе диссипативных сил и моментов; 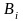– диссипативная сила (или момент), Н; 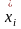– скорость (или угловая скорость), м/с; t – время, с.

Если система линейна, то

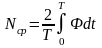; Вт

где Ф – диссипативная функция;

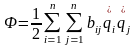
где n – число степеней свободы; 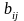– элемент матрицы коэффициентов сопротивления; 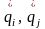– обобщенные скорости, м/с.

При разработке новой вибрационной машины расчет мощности, необходимой для поддержания вибрации, представляет трудную задачу. Такой расчет должен основываться на заданных диссипативных сопротивлениях, но о них, как правило, нет отчетливых представлений. Регулярные методы расчета диссипативных характеристик создаваемой машины обычно отсутствуют. Даже экспериментальные исследования далеко не всегда вносят достаточную ясность. Поэтому возможны серьезные просчеты в мощности двигателя при создании новой машины. Кроме того, факторы, определяющие рассеяние энергии вибрации, зачастую изменяются в довольно широких пределах. В некоторых случаях такие изменения представляют собой закономерные следствия работы машины, а иногда они вызываются случайными обстоятельствами.

По изложенным причинам нередко единственным надежным критерием является максимум средней мощности, которая может быть реализована вибровозбудителем в данных условиях. Более того, в ряде случаев максимум средней мощности практически достигается, и поэтому названный критерий становится необходимым и достаточным.

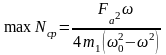; Вт

где F_a – амплитуда силы, Н;  – требуемая угловая частота вибрации, рад/с; m₁ – масса исполнительного органа, кг; ₀ – собственная угловая частота недемпфированной системы, рад/с.

Рассчитаем среднюю максимальную мощность на примере центробежного самобалансного вибровозбудителя применительно к нашему случаю.

Рис. 93. Расчетная схема вибропривода рыбовода набивочной машины: 1 – дебаланс; 2 – шестерня; 3 – рыбовод; 4 – пружина

Вибратор – самобаланс является механизмом в полном смысле этого слова. Он состоит из трех звеньев с двумя вращательными парами 5-го класса и одной кинематической пары 4-го класса.

Теоретические работы, рассматривающие вибрационные машины как системы, совершающие вынужденные колебания, сводят анализ работы вибрационной машины к изучению движения одного ведомого звена, т. е. звена, движение которого обеспечивает выполнение полезной механической работы. Обычно для получения уравнений вынужденных колебаний массы m₁ при воздействии на нее другого звена – дебаланса с массой m₀ заменяется силой, не зависящей от движения самой массы m₁, при этом закон изменения возмущающей силы принимается зависящим только от времени. Во всех работах теоретического или расчетного порядка по этому вопросу принимают, что сила инерции самобалансного вибратора, вызывающая колебания массы m₁, постоянна по величине и равна центробежной силе относительного вращательного движения ротора.

Самобалансный вибровозбудитель может работать в трех режимах работы: дорезонансный ( < ₀), резонансный ( = ₀), зарезонансный ( > ₀). Сравнивая между собой режимы работы вибромашин, можно сделать вывод, что наилучшим режимом работы является зарезонансный, т. к. при нем возникают минимальные усилия, действующие на пошипники и упругие связи. Однако этот режим обладает весьма существенным недостатком, заключающимся в том, что при пуске и выбеге система неизбежно должна переходить область резонанса и в этот момент возникают весьма большие амплитуды колебаний, вызывающие, в свою очередь весьма большие воздействия на упругие связи вибромашины. Часто переход резонансной области сопровождается жесткими ударами, являющимися причиной поломки пружин и упругих элементов конструкции вибромашины.

В машинах, работающих на дорезонансном режиме, этот недостаток отсутствует, но усилия, действующие на подшипники и упругие связи, в этом случае при установившемся движении настолько велики, что этот режим почти не пригоден для работы.

Резонансный режим обладает недостатками и того и другого режимов работы и его следует всячески избегать. Этот режим опасен тем, что, проектируя машину для работы на зарезонансном режиме с рессорными упругими связями, всегда можно получить резонансный режим, так как обычно собственная частота колебаний определяется только в одном направлении, а именно – в направлении меньшей жесткости рессоры.

Поэтому необходимо рассмотреть зарезонансный режим работы вибромашины.

Для центробежных вибровозбудителей модуль вынуждающей силы принимают равным модулю центробежной силы, развиваемой дебалансами:

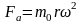; Н

где – масса дебаланса, кг; – эксцентриситет относительно оси вращения массы дебаланса, м;  – угловая частота вынужденной вибрации, рад/с.

Учитывая, что в зарезонансном режиме работы 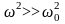, можно записать уравнения вынужденных колебаний рыбовода с частотой возмущающей силы

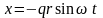
где 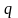– отношение масс,

,

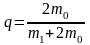откуда абсолютное отклонение рыбовода от среднего положения, т. е. амплитуда колебания

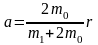, м

Отсюда можно найти эксцентриситет массы дебаланса относительно оси вращения

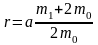, м

Масса исполнительного органа

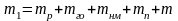, кг

где 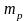– масса рыбовода, кг; – масса гибких органов, кг; 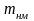– неучтенная масса, кг; 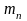– присоединительная масса, кг; – масса узлов вибровозбудителя за исключением дебалансов, кг.

Определим собственную частоту колебаний вибровозбудителя:

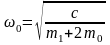, рад/с

где с – жесткость упругой системы, кг/м.

Сила сжатия пружи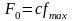н:

, Н

где 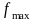– полная деформация пружин, м.

Центробежная сила определяется по формуле:

, Н.

Приравняв силу сжатия пружин и центробежную силу, получим формулу для определения жесткости пружинной системы:

, кг/м.

Полная деформация пружин будет равна:

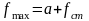, м

где 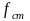– статическая деформация пружин, м.

Статическая деформация пружин определяется

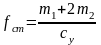, м,

где 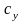– жесткость пружин в направлении оси у, кг/м.

Определим максимальную среднюю мощность, необходимую для поддержания установившейся вибрации:

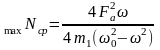, Вт

Для сравнения мощности различных типов вибровозбудителей нам необходимо определить удельную мощность

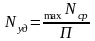, Вт·час/кг

где П – производительность машины, кг/час.