6.3. Реологические свойства обрабатываемых продуктов

При теоретическом исследовании процесса виброперемещения большинство исследователей моделируют массовый груз материальной частицей. Теория движения частицы по вибрирующей плоскости разработана очень подробно. В ней считается известным движение рабочего органа вибротранспортера. Рассматриваются дифференциальные уравнения совместного движения рабочего органа и частицы, из которых определяют движение частицы и движение рабочего органа. Далее результаты теории обычно применяются к расчету средней скорости движения на вибрирующей плоскости не одной частицы, а целого слоя частиц.

Проведенные экспериментальные исследования процессов вибрационного перемещения насыпных грузов доказали, что в действительности слой частиц, расположенных на вибрирующей плоскости, движется гораздо сложнее, чем одна частица и позволили получить истинные законы движения отдельных частиц и монослоев груза.

Взаимодействие рабочего органа машины с обрабатываемой средой (в процессах гомогенизации, рассева, измельчения, резания, транспортирования и пр.) в целях отыскания оптимальных параметров технологического режима следует рассматривать с позиций механики и реологии.

Методами механики описывается взаимодействие рабочего органа с обрабатываемой средой как механическим объектом, реология же позволяет вскрыть внутренние процессы в среде.

Для решения реологических задач математическими методами созда­ются феноменологические модели исследуемых сред. Феноменологические модели позволяют качественно достоверно оха­рактеризовать реологическое поведение среды и являются исходной основой для составления реологических уравнений.

Реологические свойства различных сред могут быть фундаментальны­ми и сложными. К фундаментальным реологическим свойствам приня­то относить упругость, вязкость и пластичность. К перечисленным свойствам следует еще добавить прочность. Сложные реологические свойства являются комбинацией фундаментальных свойств.

В сложной феноменологической модели простейшие реологические тела могут быть соединены друг с другом последовательно и параллельно. Простейшие реологические тела, соединен­ные последовательно, действуют как звенья одной цепи и должны поэтому воспринимать одинаковые напряжения, а деформация всей последовательности реологических тел будет равна сумме деформаций каждого тела.

При параллельном соединении простейшие реологические тела испытывают одинаковые деформации; общее напряжение, которое воспринимает их комбинация, представляет собой сумму напряжений, воспринимаемых каждым отдельным простейшим реологическим телом.

Так формулируются принципы построения феноменологических моделей из реологических тел. Составим реологические уравнения для различных комбинаций простейших реологических тел.

Упругое фундаментальное реологическое тело, изображаемое пружиной, представляется зависимостью между деформацией и напряжением. Зависимость этой силы от деформации линейная и на графике изображается прямой линией, выходящей из начала координат.

Реологическое уравнение упругого тела (рис. 44)

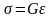
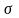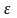здесь – напряжение в упругом теле; – модуль упругости; – деформация.

Рис.44. Простейшее упругое реологическое тело.

Если имеется n простейших реологических упругих тел и они соединены последовательно (рис. 45), то

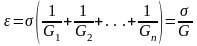
где 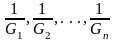– коэффициенты податливости 1-го, 2-го, n-го реологических тел; – приведенный модуль упругости.

Рис.45. Последовательное соединение упругих тел.

Если простейшие упругие тела соединены параллельно (рис.46), то

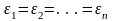или

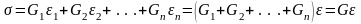
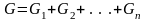
Рис.46. Параллельное соединение упругих тел.

Вязкое реологическое тело изображается в виде цилиндра с поршнем. Такой символ вязкого реологического тела принят в связи с тем, что подобные сопротивления испытывает тело, движущееся в жидкости, например поршень в цилиндре, заполненном жидкостью. Сила вязких сопротивлений пропорциональна скорости, с которой осуществляется деформация тела, и зависит от коэффициента вязких сопротивлений жидкости.

Зависимость этой силы от скорости деформации линейная и на графике изображается прямой линией, выходящей из начала координат.

Реологическое уравнение вязкого реологического тела (рис. 47)

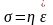
Рис. 47. Вязкое простейшее реологическое тело

Если n простейших реологических вязких тел соединены последовательно (рис. 48), то

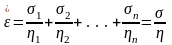
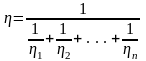
Рис. 48. Последовательное соединение вязких реологических тел

Если n простейших реологических вязких тел соединены параллельно (рис. 49), то

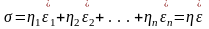
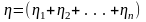
Рис. 49. Параллельное соединение вязких реологических тел

Пластическое реологическое тело изображают в виде двух скользящих одна по другой пластинок. Усилие, необходимое для деформации этого тела, не зависит ни от величины деформации, ни от скорости деформации. Оно определяется некоторой предельной силой, при достижении которой начинается пластическая деформация тела. График этой силы представляет собой линию, параллельную оси деформации.

Реологическое уравнение простейшего пластического реологического тела (рис.50)

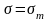
где 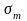– предел текучести.

Рис. 50. Пластическое прстейшее реологическое тело

Как при последовательном, так и при параллельном соеди­нении n простейших пластических реологических тел, в процессе деформации все они испытывают одинаковые смеще­ния. В силу этого в обеих схемах их соединения напряжения, испыты­ваемые комбинацией простейших реологических тел, равны сумме на­пряжений, воспринимаемых каждым отдельным элементом

.

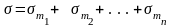Известно, что ряд материалов и сред обладает свойством упрочнения. Сущность процесса упрочнения состоит в том, что предел текучести (момент перехода от упругих деформаций к пластическим) возрастает с увеличением деформации.

Для описания процесса упрочнения среды может быть использована усложненная пластическая феноменологическая модель (рис. 51).

Рис. 51. Пластическая феноменологическая модель

Модель состоит из нескольких соединенных последовательно с зазором простейших пластических тел, имеющих различные пределы текучести. С ростом деформации, т. е. выбиранием зазоров, все большее число тел будет вовлекаться в движение, что соответствует повышению предела текучести феноменологической пластической упрочняющейся модели. Диаграмма деформация — напряжение феноменологической модели пластической деформации имеет ступенчатый характер.

Реологическое уравнение приведенной упрочняющейся пластической модели будет иметь вид

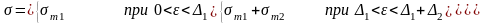
где 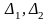– зазоры между реологическими телами

Для описания процесса пластической деформации с упрочнением мо­жет быть использована также модель типа клина (рис.52), реологическое урав­нение которой имеет вид

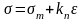
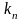– коэффициент упрочнения в процессе пластической деформации.

Рис. 52. Пластическая феноменологическая модель в виде клина

Реальные среды обладают всеми реологическими свойствами, хотя и в различной степени.

Классические феноменологические модели предназначены для изучения поведения исследуемых сред в условиях статического деформирования.

В вибрационных машинах транспортируемые и обрабатываемые среды подвергаются динамическим воздействиям, процесс деформирования протекает при значительных ускорениях. При этом силы инерции оказываются соизмеримыми с упругими, вязкими и пластическими сопротивлениями деформированию. Поэтому в феноменологических моделях, предназначенных для описания реальных сред в условиях вибрационных воздействий, необходимо учитывать их инерционные свойства. Для исследования поведения реальных сред в условиях периодических воздействий получили развитие методы вибрационной реологии.

Основное отличие вибрационной реологии от реологии традиционной состоит в том, что все реологические тела – упругие, вязкие и пластические – рассматриваются как носители двух свойств – своего основного и инерционного. Например, не просто упругое тело, а упругоинерционное, не просто вязкое, а вязкоинерционное.

Рис. 53. Упругоинерционое реологическое тело

Рис. 54. Вязкоинерционное реологическое тело

Рис. 55. Пластично-инерционное реологическое тело

В упругом теле соотношение между деформацией x, жесткостью k, и деформирующей силой Fsin t при периодическом гармоническом нагружении определяется зависимостью

.

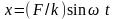В упругоинерционном теле, собственная частота колебаний которого p, деформация определяется также членом 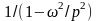, так называемом коэффициентом усиления

,

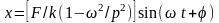и смещена на угол =arctg(n/) по отношению к деформирующей силе.

Сравнивая закономерности деформации вязкого и вязкоинерционного тел, видим, что скорость деформации вязкоинерционного тела меньше в раз. Разница в скоростях деформации возрастает с умень­шением вязких сопротивлений и повышением частоты приложения деформирующей нагрузки. Угол сдвига фаз между деформацией и деформирующей силой воз­растает при увеличении коэффициента вязких сопро­тивлений и снижении частоты.

В инерционно-пластичном теле, характеризующемся сопротивлением пластическому сдвигу F_п, соотношение между деформацией и деформирующей нагрузкой дает­ся следующим приближенным выражением:

.

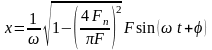Деформация смещена относительно деформирующей нагрузки на угол

.

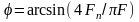Из приведенной зависимости видно, что для обеспе­чения деформации инерционно-пластичного тела перио­дической силой необходимо, чтобы амплитудное значе­ние этой силы превышало силу сопротивления пласти­ческому сдвигу. Для получения более или менее значительных деформаций необходимо, чтобы это превышение было существенным. Угол сдвига фаз между деформацией и деформирующей силой опреде­ляется соотношением между величинами сопротивле­ния пластическому сдвигу и деформирующей силой.

Задачей вибрационной реологии является описание зависимости реологических параметров обрабатываемой среды от параметров вибрации – амплитуды и частоты.

Решение этой задачи включает следующие этапы:

– описание реологических свойств среды;

– исследование связей между реологическими параметрами среды и амплитудно-частотной характеристикой вибромашины;

– выбор параметров вибрации, при которых происходит наибольшее разрушение связей в структуре среды;

– решение дифференциальных уравнений движения среды;

– выбор условий возникновения относительного движения среды;

– поиск условий, предъявляемых к конструкции вибромашины, обеспечивающих оптимальную обработку среды;

В настоящее время уже сформировались некоторые общие принципы построения феноменологических моделей. Разработаны методы определения параметров составляющих их реологических тел. Эту операцию называют идентификацией модели с реальным объектом. В качестве исходных для идентификации модели могут быть использованы результаты экспериментов. При разработке моделей слоя ранее стремились обеспечить равенство теоретической и экспериментальной средних скоростей виброперемещения. Это условие является необходимым для оценки совершенства модели, но не достаточным. Более достоверный критерий совершенства модели – соответствие теоретического и экспериментального законов движения модели и слоя.